Luobuyu's Blog

0%

137.只出现一次的数字II

发表于 分类于 ， ， 热度： ℃ 评论：
本文字数： 2.1k 阅读时长 ≈ 2 分钟
类似直接异或的，使用位运算统计。

137.只出现一次的数字II

题目描述：

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。

数据范围：

$1\le nums.len \le 3\times10^4;-2^{31} \le nums[i] \le 2^{31} - 1$

题解：

首先最简单版本，某个元素出现一次，其余的都是两次。则直接求异或和，出现两次的都异或抵消了，只剩下出现一次的数字。

思考，是因为异或是个模 $2$ 的运算，每次 $0\rightarrow 1\rightarrow 0\cdots\rightarrow 1$ 。所以才能够满足上题，刚好抵消。

但是这个题是一个元素出现一次，其余的都是3次。如果有一个模 $3$ 的运算，则可以实现出现 $3$ 次的都抵消，只剩下一个出现 $1$ 次的。可以统计每个位上， $1$ 出现的次数，然后模除 $3$ ，余数就是单次出现的元素该位的数字。（并且模除 $3$ 之后只能是 $1$ 或 $0$ ，因为不可能出现某一位是 $2$ 。）这个方法可以做任何类型的，某个数出现 $m$ 次，其他的都是 $n$ 次。则可以先统计数目，然后模除 $n$ 再除以 $m$ 。

也可以使用类似状态机的方法。各个二进制位的位运算规则相同，因此只需要考虑一位即可。对于所有数组中的某一个二进制位 $1$ 的个数，存在 $3$ 种状态，即对 $3$ 的余数为 $0,1,2$ 。如果该位为 $1$ 则 $0\rightarrow 1\rightarrow 2 \rightarrow 0$ 。如果该位是 $0$ 则状态不变。

因为一位二进制只能表示两个状态，不能表示三个状态，因此使用两位 $ab$ 表示，则 $00\rightarrow 01 \rightarrow 10 \rightarrow 00$ 。接下来需要推导转换计算公式。

（只针对一位的运算规则）

  • 异或运算：x ^ 0 = x, x ^ 1 = ~x
  • 与运算：x & 0 = 0, x & 1 = x

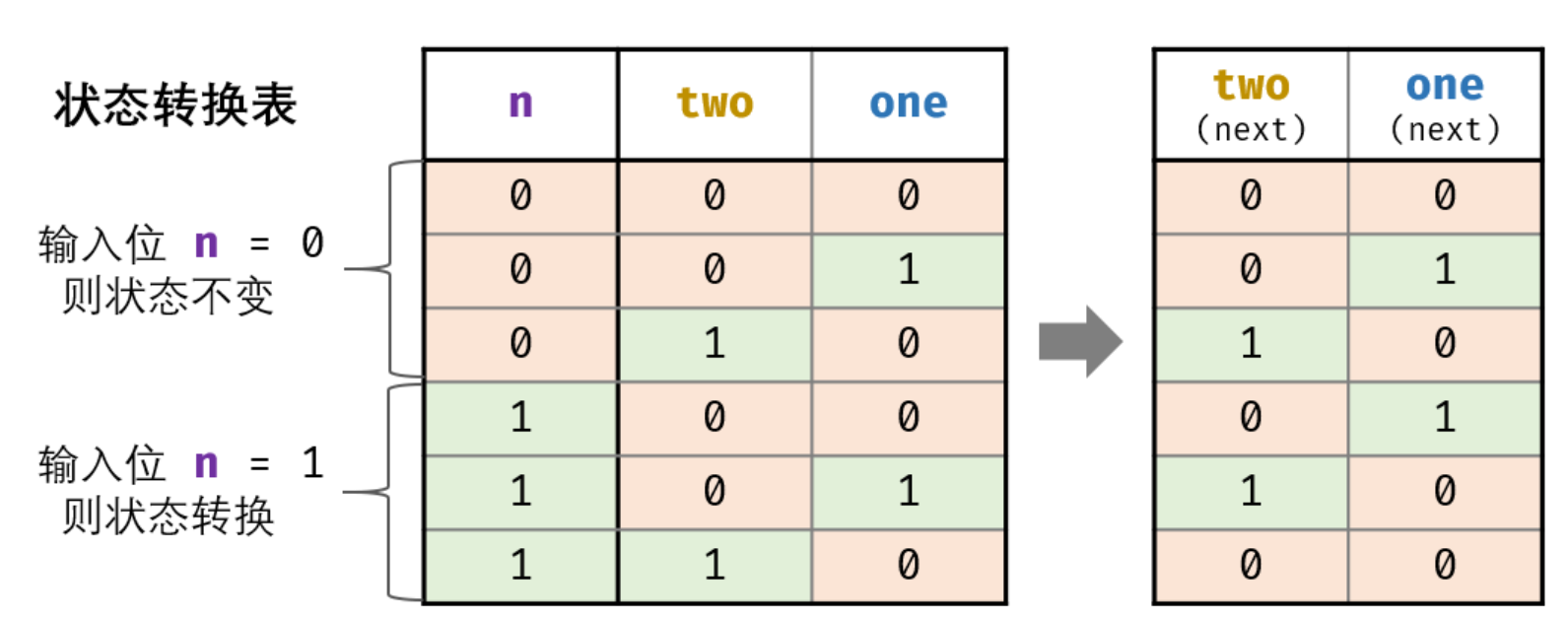
image-20231016162104529

有两种方法求转换公式。

一、使用公式转换（观察）

太过于麻烦，不如直接真值表。

二、使用真值表

a = ~n & a & ~b + n & ~a & b

b = ~n & ~a & b + n & ~a & ~b = ~a & (~n & b + n & ~b) = ~a & (n ^ b)

这只是某一位上的规则，所有位上规则都是一样的，可以直接套用。

第三种类型，某两个数出现了一次，其他的数都出现了两次。假设这两个数是 $x1,x2$ 。

则通过异或和可以得到 x1 ^ x2。首先 x1 ^ x2 != 0。因为等于 $0$ 说明二者完全一样。然后找到异或和中不等于 $0$ 的一位二进制。然后根据这一位是 $0$ 或 $1$ 将所有的数字分成两类， $x1,x2$ 一定会被划分为不同类，类内其他的数字肯定都是出现了两次。因此直接分别对每类所有的数求异或和就能得到 $x1,x2$ 。 取这一位二进制时可以使用 $lowbit$ ，即 x & -x。但是注意 $INT\_MIN = 10000\cdots 000$ 。因为 $-1$ 为 $111\cdots111111$ 。当 $x = INT\_MIN$ 时， $-x$ 就会越界，因此最好使用无符号整数，或者直接使用long long。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int a = 0, b = 0, aa = 0, bb = 0;
        for(auto& x: nums)
        {
            aa = (~x & a & ~b) | (x & ~a & b);
            bb = ~a & (x ^ b);
            a = aa;
            b = bb;
        }
        return b;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
auto optimize_cpp_stdio = []()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    return 0;
}();
class Solution
{
public:
    const static int maxn = 1e5 + 10;
    const static int maxm = 1e5 + 10;
    const int INF = 0x3f3f3f3f;
    vector<int> singleNumber(vector<int> &nums)
    {
        int xorsum = 0;
        for (auto &x : nums)
            xorsum ^= x;
        long long i = (1ll * xorsum) & (-1ll * xorsum);
        int x1 = 0, x2 = 0;
        for (auto &x : nums)
        {
            if (x & i)
            {
                x1 ^= x;
            }
            else
            {
                x2 ^= x;
            }
        }
        return {x1, x2};
    }
};