强连通分量

一、定义

强连通：有向图 $G$ 中，任意两个点都可以互相到达。

强连通分量：在有向图 $G$ 的子图 $G’$ 中， $G’$ 是强连通的，即节点可以互相到达的子图。

二、原理

1.tarjan算法

DFS生成树：

有向图的 DFS 生成树主要有 4 种边（不一定全部出现）：

树边（tree edge）：示意图中以黑色边表示，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
反祖边（back edge）：示意图中以红色边表示（即 $7\rightarrow 1$ ），也被叫做回边，即指向祖先结点的边。
横叉边（cross edge）：示意图中以蓝色边表示（即 $9\rightarrow 7$ ），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点并不是当前结点的祖先。
前向边（forward edge）：示意图中以绿色边表示（即 $3\rightarrow 6$ ），它是在搜索的时候遇到子树中的结点的时候形成的。

一个强连通分量主要是由于返祖边形成的。在DFS生成树中，一些边违反了树的规则，就会出现一些性质。通过DFS的方式将边分成了在树上的边和不在树上的边。

引入变量：

$dfn[u]$ ：表示节点 $u$ 的dfs序，即在dfs时第几个被访问到的。

$low[u]$ ：表示节点 $u$ 最远能够到达的祖先，可以走非树边。

假设 $u$ 为子树的根，则子树内节点 $v$ 的 $dfn[v]$ 值严格大于 $dfn[u]$ ，因为在 $dfs$ 的过程中 $u$ 作为根先被遍历到；子树内节点 $v$ 的 $low[v]$ 值大于等于 $dfn[u]$ 。因为如果没有更远的祖先那么 $u$ 就是 $v$ 最远的祖先 $low[v] = dfn[u]$ ，否则的话 $low[v] > dfn[u]$ 。

使用dfs对图中所有的点进行搜索，维护每个节点的 $dfn$ 和 $low$ 值，让搜索到的节点入栈，打上标记。假设当前节点为 $u$ ，在搜索过程中，下一个节点 $v$ 分为以下情况：

$v$ 未被访问过：说明还在该子树中，继续向下搜索。并且更新 $low[u] = \min(low[u], low[v])$ 。因为存在 $u\rightarrow v$ ，所以 $v$ 能够到达的祖先 $low[v]$ ，也能被 $u$ 到达。
$v$ 被访问过：
1. $v$ 已经在栈中，已经被打上标记：说明遇到了祖先节点 $v$ 。并且更新 $low[u] = \min(low[u], dfn[v])$ 。
2. $v$ 没有在栈中，没有被打上标记：说明 $v$ 已经搜索完毕了， $v$ 是其他的连通分量里面的，并且已经被处理过了，所以不用对其处理了。
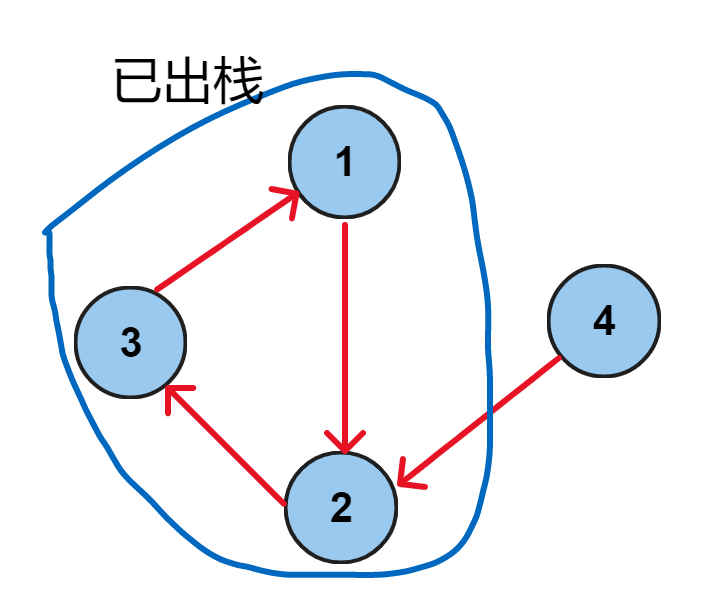
  例如 $4$ 遍历到 $2$ ， $2$ 已经被访问过，并且不在栈中，说明已经被处理了，不用管了。

因为一个节点有多个孩子分子，所以需要对所有的分支进行dfs，并且使用 $\min$ 维护 $low[u]$ 。

在一个连通分量中，有且只有一个 $u$ 使得 $dfn[u] = low[u]$ ，在回溯的过程中，即后续遍历的位置，如果满足该条件，则栈中的点出栈，直到把 $u$ 也出栈的所有的点构成一个强连通分量。

由于一个有向图不一定是连通图，所以需要对所有的点dfs。总体时间复杂度为 $O(n + m)$ 。

单个的点，dfs树上的不在强连通分量中的点每个都是一个单独的连通分量。

三、代码

int dfn[maxn], low[maxn], dfn_clock = 0;
int st[maxn], top = -1;
bool vis[maxn];
int scc_id[maxn], scc_cnt = 0;
void tarjan(int u)
{
    dfn[u] = low[u] = ++dfn_clock;
    vis[u] = true;
    st[++top] = u;
    for (int i = 0; i < g1[u].size(); ++i)
    {
        int v = g1[u][i];
        if (!dfn[v])
        {
            tarjan(v);
            low[u] = min(low[v], low[u]);
        }
        else
        {
            if (vis[v])
                low[u] = min(low[u], dfn[v]);
        }
    }
    if (low[u] == dfn[u])
    {
        ++scc_cnt;
        while (true)
        {
            scc_id[st[top]] = scc_cnt;
            vis[st[top]] = false;
            if (st[top--] == u)
                break;
        }
    }
}

例题：

P3387 【模板】缩点 | Luobuyu’s Blog

参考链接：

强连通分量

tarjan算法求割点与桥

tarjan求强连通分量+缩点+割点/割桥（点双/边双）以及一些证明