题目描述:
给定一组 $n$ 个人,将每个人分到一个组,其中有矛盾的不能分到同一组。是否可以将所有人分成两组。
数据范围:
$1\le n \le 2000$
题解:
二分图检测,可以使用2color染色法,也可以使用种类并查集。
2color:
使用dfs或者bfs染色,当前点染 $0$ ,邻接点染 $1$ 。如果遇到访问过的点,判断一下染色是否相同,如果相同说明不能划分为二分图。
种类并查集:
开虚点,对每个点开一个虚点表示对立关系。实际操作时开2倍数组大小即可。如果 $u,v$ 是朋友,则 $unite(u,v), unite(u + n, v + n)$ 。如果 $u,v$ 是敌人则 $unite(u, v + n),unite(u + n, v)$ 。使用 $u +n$ 表示不选择 $u$ 。如果有一条边 $u, v$ 连接在了一起,说明不能划分为二分图,否则的话就 $unite(u, v + n),unite(u + n, v)$ 。
种类并查集维护的是传递性关系,比如敌人的敌人是朋友,总归是传递之后可以放入同一个集合中。
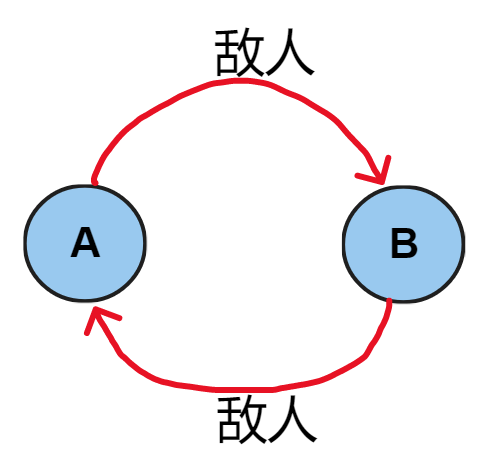
也可以维护多个集合的传递关系,并查集的大小要开更多倍,维护几个开几倍。例如 P2024.食物链
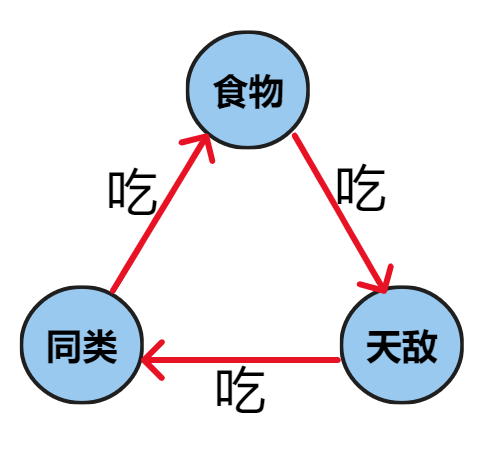
但是 $a \neq b,b\neq c$ 这种不能维护。因为 $a\neq b,b\neq c$ 不能推出 $a=c$。例如 990.等式方程的可满足性
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| class Solution
{
public:
const static int maxn = 1e5 + 10;
const static int maxm = 1e5 + 10;
const static int INF = 0x3f3f3f3f;
bool ok = true;
vector<bool> vis;
vector<bool> color;
vector<vector<int>> g;
void dfs(int u)
{
if (!ok)
return;
vis[u] = true;
for (int i = 0; i < g[u].size(); ++i)
{
int v = g[u][i];
if (vis[v])
{
if (color[u] == color[v])
ok = false;
}
else
{
color[v] = !color[u];
dfs(v);
}
}
}
bool possibleBipartition(int n, vector<vector<int>> &dislikes)
{
g.resize(n);
vis.resize(n);
color.resize(n);
for (int i = 0; i < dislikes.size(); ++i)
{
g[--dislikes[i][0]].emplace_back(--dislikes[i][1]);
g[dislikes[i][1]].emplace_back(dislikes[i][0]);
}
for (int i = 0; i < n; ++i)
{
if (!vis[i])
{
dfs(i);
}
}
return ok;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| class Solution
{
public:
const static int maxn = 1e5 + 10;
const static int maxm = 1e5 + 10;
const static int INF = 0x3f3f3f3f;
struct UF
{
vector<int> fa;
UF(int n) : fa(n)
{
for (int i = 0; i < n; ++i)
fa[i] = i;
}
int find(int u)
{
return u == fa[u] ? u : fa[u] = find(fa[u]);
}
void unite(int u, int v)
{
int up = find(u);
int vp = find(v);
if (up != vp)
fa[up] = vp;
}
bool connect(int u, int v)
{
return find(u) == find(v);
}
};
bool possibleBipartition(int n, vector<vector<int>> &dislikes)
{
UF uf(n * 2);
for (int i = 0; i < dislikes.size(); ++i)
{
int u = dislikes[i][0] - 1, v = dislikes[i][1] - 1;
if (uf.connect(u, v))
return false;
uf.unite(u, v + n);
uf.unite(v, u + n);
}
return true;
}
};
|

