题目描述:
有 $N$ 个物品和一个容量是 $V $ 的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
如下图所示:
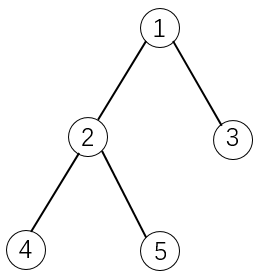
如果选择物品5,则必须选择物品 $1$ 和 $2$ 。这是因为 $2$ 是 $5$ 的父节点, $1$ 是 $2$ 的父节点。
每件物品的编号是 $i$ ,体积是 $v_i$ ,价值是 $w_i$ ,依赖的父节点编号是 $p_i$ 。物品的下标范围是 $1\cdots N$ 。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 $N$ , $V$ 用空格隔开,分别表示物品个数和背包容量。
接下来有 $N$ 行数据,每行数据表示一个物品。
第 $i$ 行有三个整数 $v_i,w_i,p_i$ ,用空格隔开,分别表示物品的体积、价值和依赖的物品编号。
如果 $p_i=−1$ ,表示根节点。 数据保证所有物品构成一棵树。
输出格式
输出一个整数,表示最大价值。
数据范围:
$1\le n, v\le 100, 1\le v_i, w_i \le 100$
题解:
使用 $dp[u][j]$ 表示节点 $u$ 分配的体积为 $j$ 能得到的最大价值。因为选择 $u$ 的孩子节点时,必须要选 $u$ ,因此可以先初始化 $dp[u][v[u]\cdots m] = w[u]$ 。
然后枚举节点 $u$ 分配的体积 $j$ , $m\ge j \ge v[u]$ ,因为小于 $v[u]$ 的连 $u$ 都放不下,最大价值是 $0$ 。然后枚举分给孩子节点的体积 $k$ , $0\le k \le j - v[u]$ 。因为 $u$ 必须要占用 $v[u]$ 。
注意 $j$ 需要倒序枚举,因为 $dp[u][j]$ 需要用到 $dp[u][j - k]$ 。需要用到前面的结果。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| using namespace std;
using namespace FAST_IO;
const ll mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF_LL = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-5;
const int maxn = 1e3 + 10;
const int maxm = 1e5 + 10;
int t, n, m, k;
vector<int> g[maxn];
int dp[maxn][maxm];
int a[maxn][2];
void dfs(int u)
{
for (int j = a[u][0]; j <= m; ++j)
dp[u][j] += a[u][1];
for (int i = 0; i < g[u].size(); ++i)
{
int v = g[u][i];
dfs(v);
for (int j = m; j >= a[u][0]; --j)
{
for (int k = 0; k <= j - a[u][0]; ++k)
{
dp[u][j] = max(dp[u][j], dp[u][j - k] + dp[v][k]);
}
}
}
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
ios::sync_with_stdio(false);
cin.tie(0);
read(n, m);
int root;
for (int i = 1, p, v, w; i <= n; ++i)
{
read(v, w, p);
a[i][0] = v, a[i][1] = w;
if (p == -1)
{
root = i;
continue;
}
g[p].emplace_back(i);
}
dfs(root);
cout << dp[root][m] << endl;
return 0;
}
|
