题目描述:
给出一个长度为 $n$ 的数组,预先按照升序排列,在下标 $k$ ,经过旋转之后得到新的数组 $[nums[k], …, nums[n-1], nums[0],…, nums[k-1]]$ 。给出一个元素值互不相同的数组 nums,找出其中最小的元素。时间复杂度限制 $O(\log(n))$
数据范围:
$1\le n\le 5000$
题解:
旋转之后的数组满足,观察发现前一段的都大于 $nums[0]$ ,后一段的都小于 $nums[0]$ 。或者前一段的都大于 $nums[n-1]$ ,后一段的都小于 $nums[n-1]$ 。可以根据这个进行二分搜索。如果 $nums[mid]$ 大于 $nums[0]$ ,则 $l = mid + 1$ ;否则 $r = mid - 1$ 。
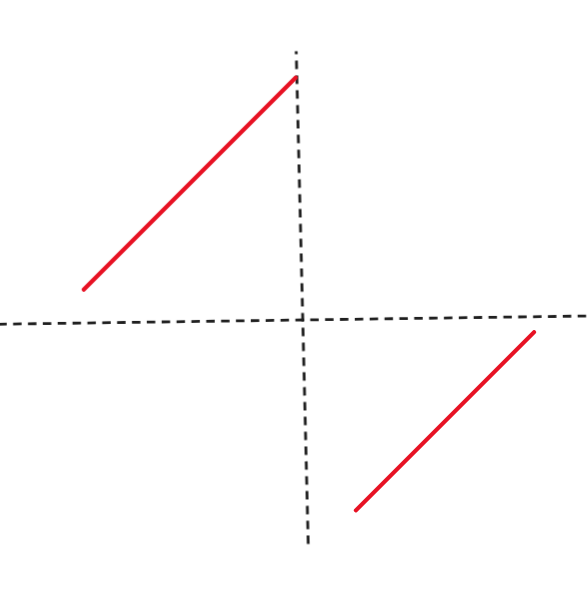
二分查找如果写成三段的形式 $[l, mid - 1], mid, [mid + 1, r]$ 需要判断 $[l,mid - 1]$ 或者 $[mid + 1, r]$ 能不能划分出来。这个题目里面如果不和 $nums[0]$ 或 $nums[n-1]$ 比较,和 $nums[r]$ 比较,就会遇到这种情况。
一般情况下会写成
1
2
3
4
5
6
7
8
9
10
11
12
13
| int l = 0, r = n - 1, ans = -1, mid;
while(l <= r)
{
mid = (l + r) >> 1;
if(nums[mid] > nums[r])
l = mid + 1;
else
{
ans = mid;
r = mid - 1;
}
}
|
但是当 $nums[mid] <= nums[r]$ 的时候,如果 $nums[mid-1]$ 大于了 $nums[mid]$ 说明 $nums[mid]$ 已经是最优解了,此时 $r = mid-1$ 会跳过最优解,跑到前一段去。二分搜索应该一直留下最优解可能存在的区间,结果留下的不是最优解可能在的区间,所以会出现问题。这时就需要加特殊的判断,如果能分出 $[l,mid-1]$ 下一次就搜索该区间,如果已经找到了最优解直接返回。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| int l = 0, r = n - 1, mid, ans = -1;
while (l <= r)
{
mid = l + r >> 1;
if (nums[mid] > nums[r])
{
l = mid + 1;
}
else if (nums[mid] <= nums[r])
{
ans = mid;
if (mid - 1 >= l && nums[mid - 1] < nums[mid])
r = mid - 1;
else
break;
}
}
|
也可以使用分两段的二分搜索查找最优解。分两段的循环条件是 $l < r$ 保证了最后返回时 $l=r$ ,可以直接得到最优解。并且由于最后一次访问时 $r = l + 1$ ,区间内部是有两个元素的,但是在最后一次循环时会再次分段,只剩下一个元素 $l=r$ ,这个元素就是答案。每次分的时候可能分成 $[l,mid-1],[mid,r]$ ,也可能分成 $[l,mid],[mid+1,r]$ 。当分成 $[l,mid-1],[mid,r]$ 时,需要令 $l = mid$ ,这个地方二分 $mid$ 时需要 $mid = r + l + 1 >> 1$ ,因为如果最后只剩两个元素,求 $mid$ 时向下取整会使得 $mid = l$ ,导致陷入死循环。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
public:
int findMin(vector<int>& nums) {
int l = 0, r = nums.size() - 1, ans = -1, mid;
while(l <= r)
{
mid = (l + r) >> 1;
if(nums[mid] < nums[0])
{
ans = mid;
r = mid - 1;
}
else
{
l = mid + 1;
}
}
if(ans == -1) ans = 0;
return nums[ans];
}
};
|
三段完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution
{
public:
int findMin(vector<int> &nums)
{
int n = nums.size();
if (nums[0] <= nums[n - 1])
return nums[0];
int l = 0, r = n - 1, mid, ans = -1;
while (l <= r)
{
mid = l + r >> 1;
if (nums[mid] > nums[r])
{
l = mid + 1;
}
else if (nums[mid] <= nums[r])
{
ans = mid;
if (mid - 1 >= l && nums[mid - 1] < nums[mid])
{
r = mid - 1;
}
else
break;
}
}
return nums[ans];
}
};
|
两段完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution
{
public:
int findMin(vector<int> &nums)
{
int n = nums.size();
if (nums[0] <= nums[n - 1])
return nums[0];
int l = 0, r = n - 1, mid;
while (l < r)
{
mid = l + r >> 1;
if (nums[mid] > nums[r])
{
l = mid + 1;
}
else
{
r = mid;
}
}
return nums[l];
}
};
|
