Luobuyu's Blog

0%

516. 最长回文子序列

发表于 分类于 ， ， 热度： ℃ 评论：
本文字数： 2k 阅读时长 ≈ 2 分钟
子序列问题，只涉及一个数组。

516.最长回文子序列

题目描述：

给你一个字符串 $s$ ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

数据范围：

$1\le s.len \le 1000$

题解：

子序列问题有两种思路：

  1. 一维dp

    类似最长上升子序列。

    定义 $dp[i]$ 表示在子数组 $arr[0,\cdots,i]$ 中，以 $arr[i]$ 结尾的目标子序列（就是所求的子序列）的长度。

    然后使用二重循环遍历更新。

  2. 二维dp

    • 涉及到两个字符串或数组时。

      定义 $dp[i,j]$ 表示在子数组 $arr[0,\cdots,i]$ 和 $arr[0, \cdots, j]$ 中，要求的目标子序列的长度。

    • 涉及到一个字符或数组时。

      定义 $dp[i,j]$ 表示在子数组 $arr[i,\cdots,j]$ 中，要求的目标子序列的长度。

      也可以使用区间 $dp$ ，直接枚举区间，枚举左端点。

    二维的一般都是需要判断 $arr[i] == arr[j]$ 的，相等时转移；不相等时取最大值。

一、直接 dp

定义 $dp[i,j]$ 表示在子数组 $s[i,\cdots,j]$ 中，回文子序列的长度。

那么可以得到转移方程

确定枚举顺序，因为 $dp[i][j]$ 需要使用到 $dp[i + 1][j]$ ，需要先得到 $dp[i + 1][j]$ ，因此第一维应该从大到小枚举；因为 $dp[i][j]$ 需要使用到 $dp[i][j - 1]$ ，需要先得到 $dp[i][j-1]$ ，因此第二维需要从前往后枚举。

二、区间 dp

直接使用区间 $dp$ ，递推方程不变，枚举方式改变

类似题目：

1312. 让字符串成为回文串的最少插入次数

需要先求出最长的回文子序列，然后 $n - len$ 就是需要插入的次数。

因为 $dp[i][j]$ 需要从 $dp[i + 1][j], dp[i][j - 1], dp[i + 1][j - 1]$ 转移过来，如图

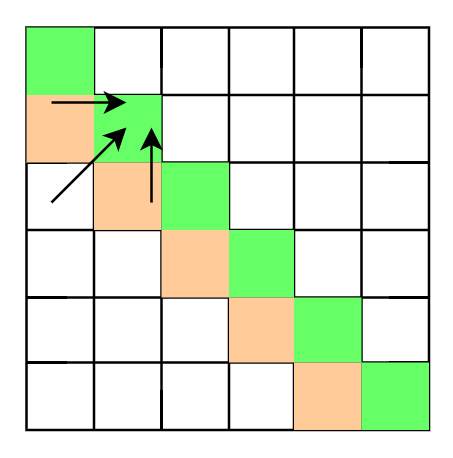
image-20230703113156316

因此可以得到两种遍历方式，一种是斜着遍历，这就是区间dp的形式。

image-20230703113500649

另一种是第二维倒着，第一维正着，这就是直接dp的形式。

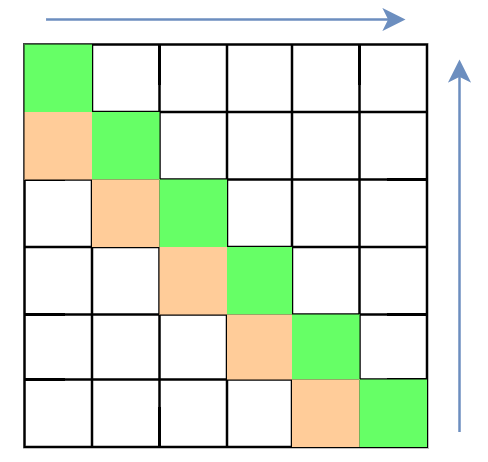
image-20230703113811574

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    const static int maxn = 1e3 + 10;
    // 找到最长的回文子序列
    int dp[maxn][maxn] = {};
    int longestPalindromeSubseq(string s) {
        int n = s.length();
        for (int i = 1; i <= n; ++i)
        {
            dp[i][i] = 1;
        }
        int ans = 0;
        for (int i = n; i >= 1; --i)
        {
            for (int j = i + 1; j <= n; ++j)
            {
                if (s[i - 1] == s[j - 1])
                {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                }
                else
                {
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[1][n];
    }
};

区间dp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    const static int maxn = 1e3 + 10;
    // 找到最长的回文子序列
    int dp[maxn][maxn] = {};
    int longestPalindromeSubseq(string s) {
        int n = s.length();
        for (int i = 1; i <= n; ++i)
        {
            dp[i][i] = 1;
        }
        int ans = 0;
        for (int len = 2; len <= n; ++len)
        {
            for(int i = 1; i + len - 1 <= n; ++i)
            {
                int j = i + len - 1;
                if (s[i - 1] == s[j - 1])
                {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                }
                else
                {
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[1][n];
    }
};