题目描述:
有三种类型的动物 $A,B,C$ ,这三种动物的食物链构成环形。
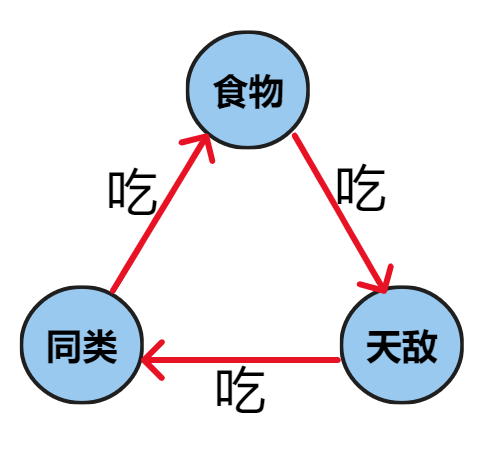
$N$ 个动物,每个动物都是其中的一种,但是并不知道是哪一种。有两种说法:
1 x y ,表示 $x$ 和 $y$ 是同类2 x y ,表示 $x$ 吃 $y$
此人对 $N$ 个动物连续说出 $K$ 句话,有真有假,当一句话满足以下三种条件之一就是假话:
- 当前的话与前面的某些真的话冲突,就是假话;
- 当前的话中 $x$ 或 $y$ 比 $N$ 大,就是假话;
- 当前的话表示 $x$ 吃 $x$ ,就是假话。
你的任务是根据给定的 $N$ 和 $K$ 句话,输出假话的总数。
数据范围:
$1\le N \le 5 \times10^4; 1\le K \le 10^5$
题解:
这个吃的关系具有传递性,可以用种类并查集解决。
有三个集合,需要开三倍空间。使用 $a,a+n,a+2n$ 分别表示 $a$ 的同类,食物,天敌集合。那么对于说的话
1 x y:如果 $(x, y + n)$ 或者 $(x,y + 2 * n)$ 在同一集合则是假话。
如果是真话则需要合并 $(x,y),(x + n, y + n),(x + 2n, y + 2n)$
2 x y:如果 $x,y+n$ , $x,y$ 在同一集合则是假话。
如果是真话则需要合并 $(x + n,y),(x + 2n, y + n),(x,y+2n)$
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
| using namespace std;
using namespace FAST_IO;
const ll mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF_LL = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-5;
const int maxn = 1e3 + 10;
const int maxm = 1e5 + 10;
int t, n, m, k;
struct UF
{
vector<int> fa;
UF(int n) : fa(n)
{
for (int i = 0; i < n; ++i)
fa[i] = i;
}
int find(int u)
{
return u == fa[u] ? u : fa[u] = find(fa[u]);
}
void unite(int u, int v)
{
int up = find(u);
int vp = find(v);
if (up != vp)
fa[up] = vp;
}
bool connect(int u, int v)
{
return find(u) == find(v);
}
};
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
ios::sync_with_stdio(false);
cin.tie(0);
read(n, k);
UF uf(n * 3 + 10);
int ans = 0;
int op, a, b;
while (k--)
{
read(op, a, b);
if (a > n || b > n)
{
ans++;
continue;
}
if (op == 1)
{
if (uf.connect(a, b + n) || uf.connect(a, b + 2 * n))
{
ans++;
continue;
}
uf.unite(a, b);
uf.unite(a + n, b + n);
uf.unite(a + 2 * n, b + 2 * n);
}
else
{
if (uf.connect(a, b + n) || uf.connect(a, b))
{
ans++;
continue;
}
uf.unite(a + n, b);
uf.unite(a, b + 2 * n);
uf.unite(a + 2 * n, b + n);
}
}
cout << ans << endl;
return 0;
}
|
