Efficient Global Optimization for Large Scaled Ordered Escape Routing
ABSTRACT
有序逃逸路由(OER)问题,是一个NP-hard问题,在PCB设计中至关重要。基于整数线性规划(ILP)或启发式算法的主要方法在引脚较少的小规模PCB上运行良好。然而,当处理大规模实例时,由于耗时的预处理,ILP策略的性能随着变量数量的增加而急剧下降。至于启发式算法,采用翻转和重路由来提高资源利用率,这经常导致时间上的违反。在本文中,我们提出了一个高效的基于ILP的密集PCB的路由引擎,考虑到特定的路由约束,同时最小化布线长度和运行时间。通过对长度的加权,我们首先将OER问题建模为一个特殊的网络流问题。然后,我们将非交叉约束从典型的ILP建模中分离出来,大大减少了积分变量的数量。此外,考虑到路由资源的拥挤情况,我们提出了ILP方法来检测拥挤情况。最后,与处理协商拥堵的传统方案不同,我们的方法是通过减少局部区域的容量,然后允许全局自动优化拥堵。与最先进的工作相比,实验结果表明,我们的算法可以在更大范围内以较少的长度解决高路由质量的情况,并将路由时间减少76%。
1.INTRODUCTION
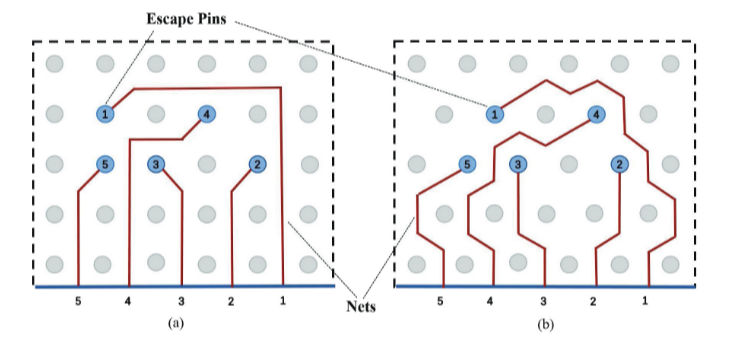
正如摩尔定律预测的那样,随着时间的推移,集成电路(IC)的集成将变得越来越密集[8]。对于印刷电路板(PCB)来说,它为IC提供了机械支撑[17],数百个引脚以规则的图案连接到IC的主体上,这增加了PCB设计工作的复杂性。作为导电路径的网络将多个IC元件的引脚连接起来。需要平面(无网络交叉)布线来完成电路。如果一个PCB层不足以以统一的方式路由所有网络,则可以使用多层PCB。PCB布线可以分为逃逸布线和长度或区域布线两部分。逃生路线将组件主体下方的引脚连接到组件的边界[11]。区域布线将线从一个零部件的边界连接到下一个零部件。根据需要,逃逸路由可以分为有序逃逸和无序逃逸[20],无序逃逸路由会导致复杂的长度路由。因此,有序逃逸路由(OER)[10, 12, 18]或同时逃逸路由[2, 13, 14]比无序逃逸路由更受欢迎。鉴于有序逃逸路由的巨大复杂性,近年来,学术界对OER问题给予了密切关注。根据引脚排列的分类,PCB可以进一步分为网格引脚阵列(GPA)和交错引脚阵列(SPA),如图1所示。逃逸引脚以一定的顺序和逆时针顺序逃逸到元件的底部边界,使其与其他元件的功能连接。当探索几种类型的网路时,复杂性就更大了。信号网、电源网和地网都是网的例子。一般来说,分离不同类型的网路是可取的,以避免交叉电缆干扰[15],这使得有序的逃逸路由更具挑战性和难度。此外,由于有这么多的引脚,作为PCB设计中最重要的关注点之一的逃逸布线,已经成为一个更容易出错的操作。传统的手工布线无法适应当今的PCB设计。然而,据我们所知,目前还没有成熟的商业或学术路由器可以在板级自动布线。在本文中,我们专注于如图1(a)所示的有序逃逸布线问题。
1.1 先前的工作
有序逃逸路由(OER)是一个NP-hard问题[5],是高速PCB路由的一个关键问题。在传统技术中,逃逸路由和总线路由经常被视为一个整体,并同时逃逸。这种情况下,不能准确地优化路由资源。2005年,Wong等人[12]提出了一种同步逃逸布线的高速算法,即多个密集元件同时进行逃逸布线,以减少中间区域的交叉点。而这种方法只能解决极小规模的路由问题,或者那些组件处于点对点模式的问题,无法充分利用组件之间的中间资源。逃逸路由和总线路由逐渐分离,实现功能设计的精细化,提高集成度[11]。
为了确保总线路由的合法性,选择有序逃逸路由为未来阶段节省更多资源。利用网络流量建模来克服先前研究中的问题。在[10]中,Luo和Wang提出将OER问题建模为平面布尔满足性问题,并使用现有的布尔满足性求解器来解决该问题。2009年,Tan等人[19]引入了一种新颖的网络流量模型建模,解决了对角容量建模的原有困难,保证了最佳解的正确性。后来在[16]中,Sattar等人建议使用网络流模型,并建立一种基于整数线性规划的路由算法[4]来优化逃逸网络的数量,并且路由比比Proteus有了很大的提高。
在论文[7]中,Jiao等人提出了有序逃生路由的三个约束条件,包括不交叉、有序和容量约束,并将经典的网络流量模型转化为最终的最小成本多商品流(MMCF)模型。然而,在辅助图构建中,这种方法引入了太多的变量,导致求解速度很差。在他们2020年的最新研究中,赵等人[9]建议使用ILP来解决OER问题。然而,这种方法将大型PCB分为小型PCB,以便它们可以独立逃逸,这并不能解决由于数量接近的引脚分散分布而产生的周围障碍物的重大问题,这很容易导致路由故障或时间违规[3]。因此,需要开发一种高效、有效的大规模有序逃逸路由算法。
1.2 本文贡献
在本文中,我们提出了一种高效的基于ILP的大规模有序转义路由引擎。我们的主要贡献总结如下。
- 为了更好地估计长度,将基本的MMCF模型应用于有序转义路由问题,并提出了一种线性规划(LP)方法来解决该问题。基于LP的最优性,我们的算法能够避免时间冲突并减少路由长度。
- 非交叉约束是从传统的ILP中提取的,这使得我们的算法能够通过将其他约束转换为LP来处理相当大的规模。
- 基于具有预定义权重函数的完全图,我们提出了一种识别局部拥塞的新方法,该方法主要依靠ILP来识别可能存在拥塞的区域。
- 我们没有分配权重来优化拥塞,而是应用LP通过减少容量来从全局角度检测更多的路由,从而有效地避免了重新调整并提高了路由质量。
没有使用基于加权的方法,使用的是减少容量的方法。
本文的其余部分组织如下。第1.3节给出了问题说明。第2节详细介绍了我们提出的算法。第3节显示了实验结果。最后,第4节结束了我们的工作。
1.3 问题描述
有序转义路由实例$R$包含一个$m \times n$ 引脚网格阵列,其中有特定的有序引脚 $p_1,p_2,\cdots,p_n$。每个引脚都有规律地排列在一系列方形网格,路由区域$\widetilde{R}$ 由$(m + 1) \times (n + 1)$个路由网格组成。OER 问题的目标是成功地将所有引脚连接到一个给定的边界,而没有任何网的交叉。此外,每个网的序列和容量是指定的。同时,总的电线长度需要在出色的路由性保证下最小化。
我们基于ILP的有序转义路由问题旨在路由所有引脚$p_1,p_2,\cdots,p_n$ 到引脚阵列边界,以使总导线长度最小化,并且每个网络必须满足以下约束:
- 非交叉:网之间不得交叉;
- 排序约束:网络必须按正确的顺序进行路由;
- 容量限制:篮网必须满足水平(H-cap)、垂直(V-cap)和对角线(D-cap)容量约束。
2.OUR ALGORITHM
图2总结了我们针对OER问题的基于ILP的算法的总体流程,该算法由三个主要步骤组成:
MMCF模型构建,
多次迭代全局路由,
基于ILP的拥塞检测策略。
我们将在以下小节中详细介绍这三个主要部分。

v1.5.1