Luobuyu's Blog

0%

115. 不同的子序列

发表于 分类于 ， ， 热度： ℃ 评论：
本文字数： 1.8k 阅读时长 ≈ 2 分钟
理清dp的枚举方式。

115.不同的子序列

题目描述：

两个字符串 $s$ 和 $t$ ，统计并返回在 $s$ 的子序列中 $t$ 出现的个数。

数据范围：

$1\le s.len, t.len \le 1000$

题解：

dp数组定义相同，如果采用不同的枚举方式，那么效率也是不一样的。

排列问题的两种视角

其中 $A_n^m$ 表示从 $n$ 个元素中取出 $m$ 个元素的排列总数。假设从 $n$ 个球（带编号），选出 $m$ 个球放到 $m$ 个盒子中去，每个盒子只能放一个。

那么就有两种思考方式：

  • 从盒子的角度看，每个盒子必须要放一个球。第一个盒子可以选任意的一个，剩下的 $m - 1$ 个盒子在 $n - 1$ 个球中选择，则

    $A_n^m = n\times A_{n - 1}^{m - 1}$

  • 从球的角度看，每个球可以选择放与不放。不放的话，需要将 $n - 1$ 个球放入 $m$ 个盒子；放的话，需要将 $n - 1$ 个球放入剩余的 $m - 1$ 个盒子。则

    $A_n^m = A_{n - 1} ^ m + m \times A_{n - 1} ^ {m - 1}$

对于本题来说，相当于从 $s$ 中取出 $t$ 个字母放到 $t$ 中去。那么也会有两种枚举方式。

第一种，从 $t$ 的角度看，先找出 $t[0]$ 在 $s$ 的什么位置，假设 $s[l1], s[l2]$ 是字符 $t[0]$ ，那么问题变成了在 $s[l1 + 1], s[l2 + 1]$ 中计算 $t[1]$ 出现的次数。

这种方式需要三重循环枚举，复杂度比较高。

第二种，从 $s$ 的角度看，对于 $s[0]$ 看能否匹配 $t[0]$ ，如果不能则需要 $s[1]$ 进行匹配；如果 $s[0]$ 可以匹配 $t[0]$ ，那么需要考虑是否使用 $s[0]$ 参与匹配。参与匹配变成了 $s[1],t[1]$ ；不参与变成了 $s[1],t[0]$ 。二者是或的关系，因此需要累加。

也可以转成递减的形式

注意初始情况：

如果 $t.len > s.len$ ，直接返回 $0$ 。

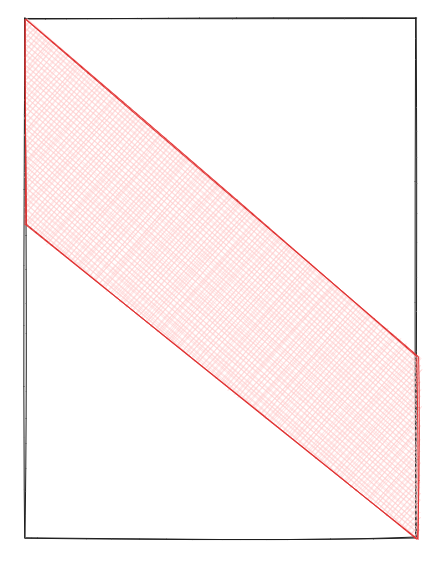
初始化 $dp[i][0] = 1$ ，因为空集也是一个子序列。发现遍历的图形是一个平行四边形。因为每个位置只与上面和左上角的有关，因此可以考虑优化。第一重循环枚举行，第二重循环枚举列的话不太方便，可以考虑交换。使用第一重循环枚举列，第二重循环枚举行，而且行宽是固定的 $n - m$ 。

即 $j \in [1, m],i \in [j, n - m + j]$

image-20230704181558340

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
auto optimize_cpp_stdio = []()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    return 0;
}();
class Solution
{
public:
    const static int maxn = 1e3 + 1;
    unsigned int dp[maxn][maxn] = {};
    int numDistinct(string s, string t)
    {
        int n = s.length(), m = t.length();
        if(n < m) return 0;
        for (int i = 0; i < n; ++i)
        {
            dp[i][0] = 1;
        }
        for (int j = 1; j <= m; ++j)
        {
            for (int i = j; i <= n - m + j; ++i)
            {
                if (s[i - 1] == t[j - 1])
                {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                }
                else
                    dp[i][j] = dp[i - 1][j];
            }
        }
        return dp[n][m];
    }
};