Luobuyu's Blog

0%

割点和桥

发表于 分类于 ， 热度： ℃ 评论：
本文字数： 1.5k 阅读时长 ≈ 1 分钟
求无向图点的割点和桥。

割点和桥

一、定义

割点和桥都是无向图中的概念。

割点：对于无向图，删除该点及其出边之后图的连通分量增加了，这个点就是割点，又称为割顶。

桥：对于无向图，删除该边之后，图的连通分量增加了，这个点就是桥。

二、原理

割点和桥都可以使用 tarjan 算法求解。

割点

使用 tarjan 算法求割点，对于割点 $u$ ，需要存在孩子节点 $v$ ，满足 $low[v]\ge dfn[u]$ ，满足该条件的为割点。特殊的是，如果一个点为根，并且有多于两棵子树，则该根节点也为割点。

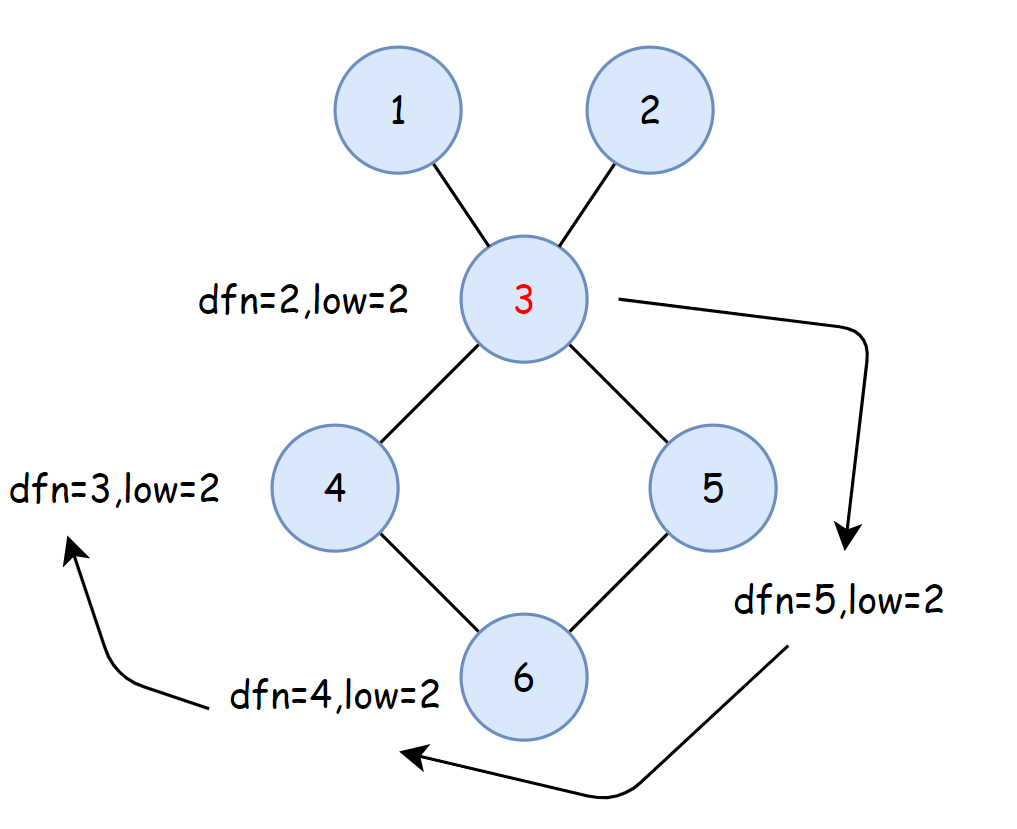
image-20230526182640427

如上图， $low[v] \ge dfn[u]$ 表示在 $u$ 为根的子树中，子树中的节点 $v$ 最远能够到达的祖先不能高于 $u$ ，最多只能到 $u$ ，因此 $u$ 显然就是一个割点。大于的情况如下所示：

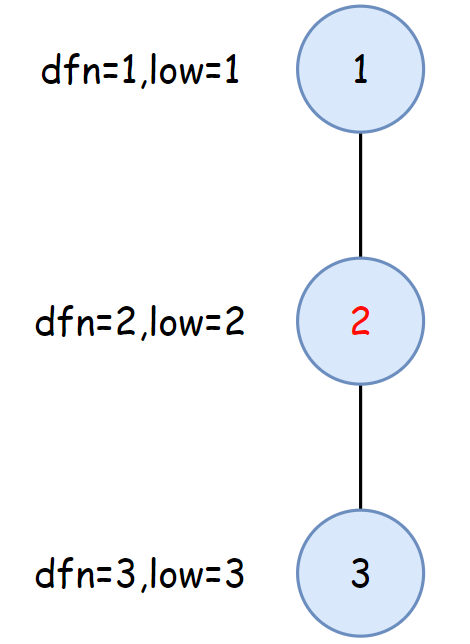
image-20230526183145773

如果为根节点，在遍历时需要记录子树的数量，在后续遍历的位置判断子树的数量是否大于 $1$ ，大于 $1$ 则为割点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
bool ans[maxn];
int dfn[maxn], low[maxn], dfn_clock = 0;
void tarjan(int u, int fa, bool isRoot)
{
    low[u] = dfn[u] = ++dfn_clock;
    int child_cnt = 0;
    for (int i = 0; i < g[u].size(); ++i)
    {
        int v = g[u][i];
        if (!dfn[v])
        {
            tarjan(v, u, false);
            low[u] = min(low[u], low[v]);
            if (!isRoot && low[v] >= dfn[u])
                ans[u] = true;
            ++child_cnt;
        }
        else
        {
            if (v != fa)
                low[u] = min(low[u], dfn[v]);
        }
    }
    if (isRoot && child_cnt >= 2)
        ans[u] = true;
}

写代码时，也可以不用 isRoot，对根节点传入 fa = u，判断根节点时只用判断 fa == u 就行了。

桥

使用 tarjan 算法求桥，对于桥 $e=\{u,v\}$ ，需要满足 $low[v] \gt dfn[u]$ ， $u$ 的孩子节点如果满足该条件则 $u\rightarrow v$ 这条边为桥。

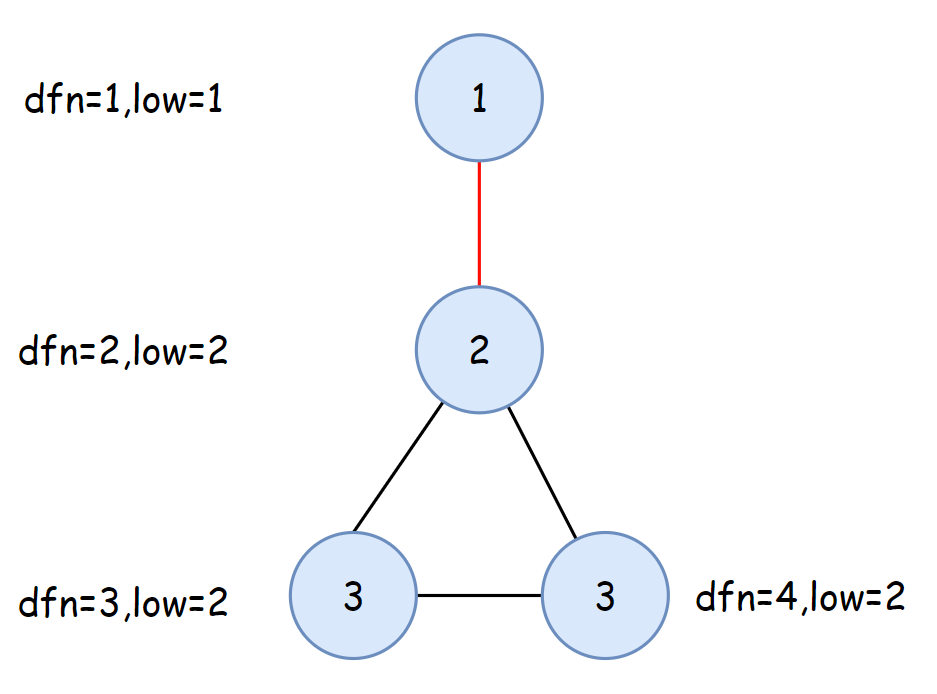
image-20230526184427352

单个的链也是桥。

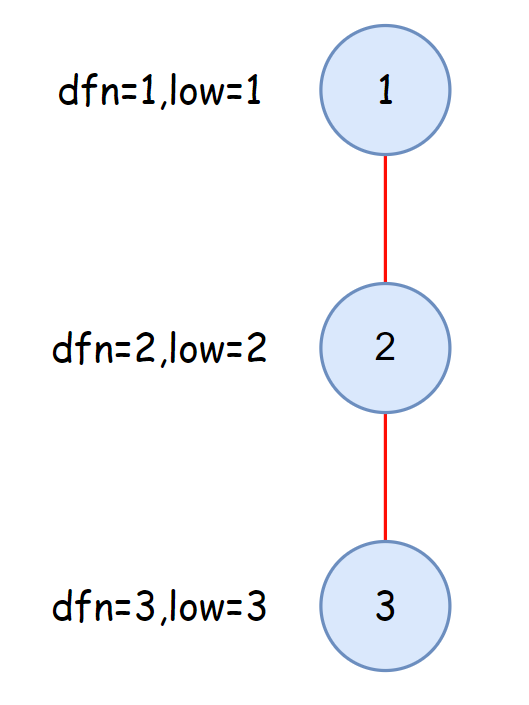
image-20230526205737346

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void tarjan(int u, int fa)
{
    dfn[u] = low[u] = ++dfn_clock;
    for (int i = 0; i < g[u].size(); ++i)
    {
        int v = g[u][i].first;
        int w = g[u][i].second;
        if (!dfn[v])
        {
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if (low[v] > dfn[u])
            {
                ans = min(ans, w);
            }
        }
        else if(v != fa)
        {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

使用链式前向星更方便一些，链式前向星可以把所有的边存起来，如果一个边是桥，可以方便的打标记。

例题：

P3388 【模板】割点（割顶） | Luobuyu’s Blog

4738.Caocao’s Bridges | Luobuyu’s Blog

参考链接：

为什么else里面不能用low[v]更新，必须得用dfn[v]

image-20230526215128331