题目描述:
给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。
你可以对数组执行 至多 k 次操作:
- 从数组中选择一个下标
i ,将 nums[i] 增加 或者 减少 1 。
最终数组的频率分数定义为数组中众数的 频率 。
请你返回你可以得到的 最大 频率分数。
众数指的是数组中出现次数最多的数。一个元素的频率指的是数组中这个元素的出现次数。
数据范围:
$1\le nums.len \le 10^5, 1\le nums[i] \le 10^9, 0\le k \le 10^{14}$
题解:
首先还是需要排序,排序之后对一个子数组来说,将所有的数操作成一样的,最少的操作次数为将所有的数都改为中位数,和上一题一样。改成中位数之后,利用前缀和,可以快速计算出来花费。
考虑使用滑动窗口,每次检查窗口大小是否合适,不合适的话移动左指针,否则移动右指针。注意数据范围,不要越界。
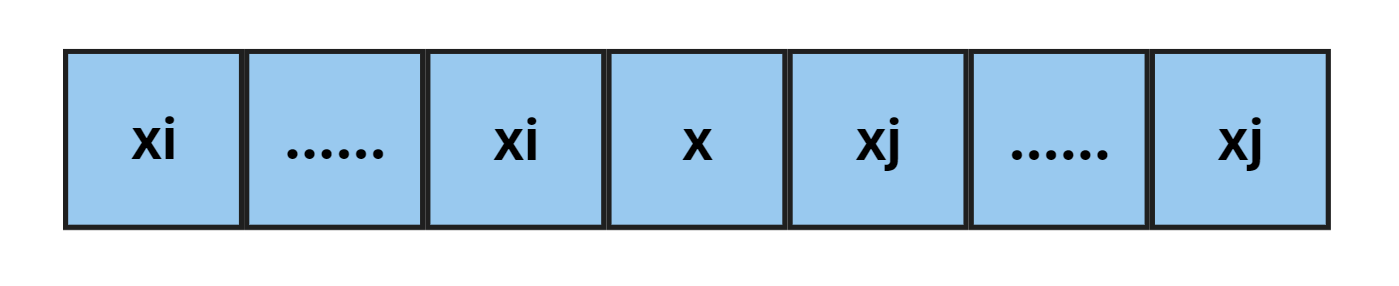
选择中位数的话,左侧代价为 $\sum x - x_i = cnt_i \times x - \sum x_i$ ,右侧代价为 $\sum x_j - x = \sum x_j - cnt_j \times x$ 。求和可以使用前缀和,这样的话可以 $O(1)$ 得到整个区间的代价。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| auto optimize_cpp_stdio = []()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
return 0;
}();
class Solution
{
public:
bool check(vector<int> &nums, vector<long long> &preSum, int l, int r, long long k)
{
int x = l + (r - l >> 1);
long long cnt = preSum[r] - preSum[x] - 1ll * (r - x) * nums[x - 1] + 1ll * (x - l) * nums[x - 1] - (preSum[x - 1] - preSum[l - 1]);
return cnt <= k;
}
int maxFrequencyScore(vector<int> &nums, long long k)
{
int n = nums.size();
sort(nums.begin(), nums.end());
vector<long long> preSum(n + 1);
for (int i = 1; i <= n; ++i)
{
preSum[i] = preSum[i - 1] + nums[i - 1];
}
int ans = 1;
int l = 1, r = 1;
for (r = 1; r <= n; ++r)
{
while (!check(nums, preSum, l, r, k))
++l;
ans = max(ans, r - l + 1);
}
return ans;
}
};
|
