Ordered Escape Routing with Consideration of Differential Pair and Blockage
1.INTRODUCTION
不同的引脚阵列:
a.grid pin array(GPA),b.staggered pin array(SPA)(不带差分对)
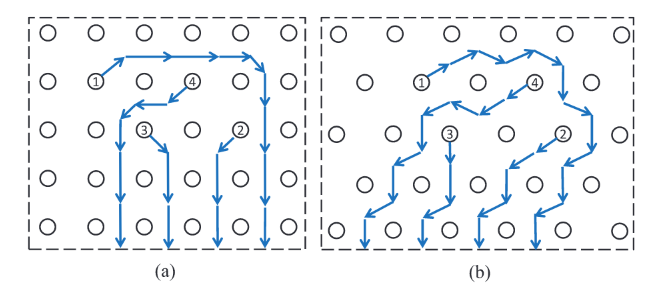
带差分对:
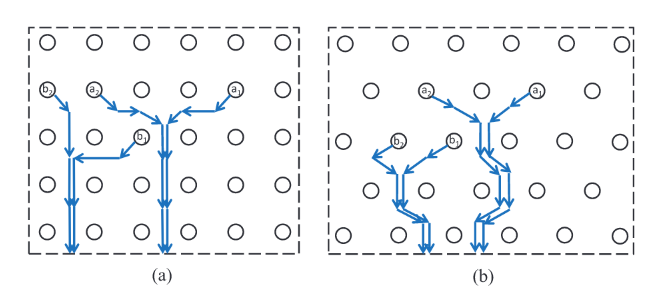
带阻塞的差分对有序逃逸示例
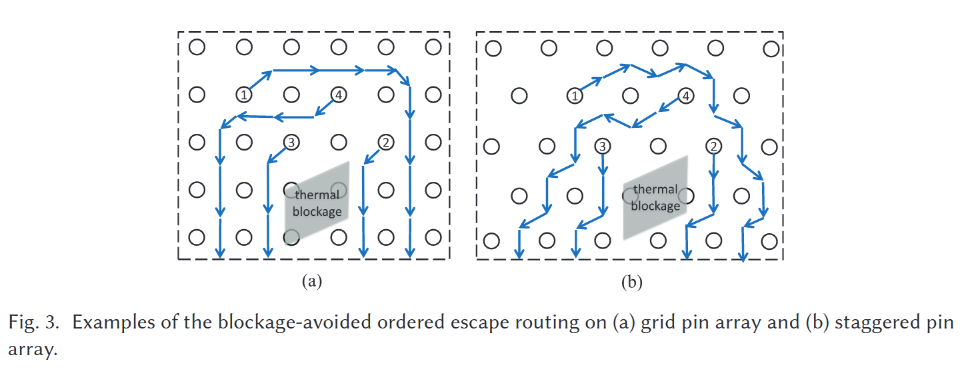
常使用网络流模型对GPA和SPA封装进行求解。
2.PRELIMINARIES
2.1 MMCF模型
最小成本多商品流(MMCF)通过单个网络以最小成本同时运输多个商品,不同的商品在单个网络中竞争弧容量所代表的资源。例如,在电话网络中,不同地点之间的呼叫必须通过相同的电话电缆进行路由,这些电话电缆的容量有限,成本不同(Ahuja等人,1993)。图4是最小成本多商品流问题的一个例子,其中源节点是V1,目的节点是V9。
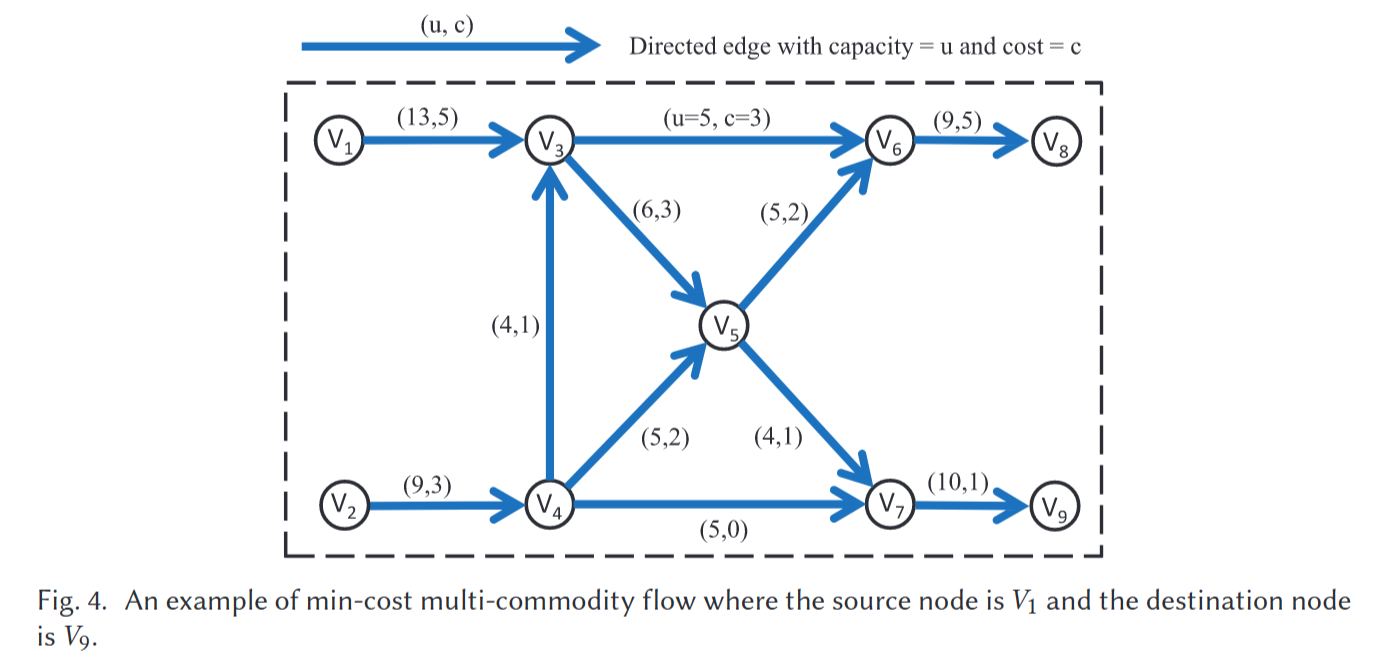

对于每条边 $link(i,j)\in A$ 和每个商品 $k \in K$ ,关联一个单位流量的成本,用 $c_{ij}^k$ 表示。每个节点 $i \in N$ 对商品 $k$ 的需求被指定为 $b_i^k$ ,其中 $b^k_i\ge 0$ 表示供应节点, $b^k_i\lt 0$ 表示需求节点。定义决策变量 $x_{ij}^k$ ,表示从节点 $i$ 和节点 $j$ 发送的商品 $k$ 的数量。
可以通过每条链路发送的所有商品的总流量,其上限为 $u_{ij}$ .
目标是为这些需求中的每一个找到通过网络的最优(即,最小成本)路由集。限制条件是,每条链路的总流量必须小于链路的容量,并且流量需求不能划分到不同的路由上,即整个连接通过一条路径进行路由。
MMCF线性规划模型如下所示:
其中,第一个约束限制了每个弧上所有商品的总流量。
第二个约束确保离开每个供应节点和进入每个需求节点的商品流量是平衡的。
第三个约束是决策变量的数据范围。
MMCF在文献中得到了广泛的讨论,因为它对各种传输和调度问题进行了建模。从算法的角度来看,MMCF激发了许多重要的想法,这些想法后来得到了更广泛的应用:例如列生成方法和Dantzig-Wolfe分解算法。在本文中,我们将有序转义路由转换为MMCF,并通过MMCF求解器进行求解。细节将在第4节中说明。
2.2 GPA封装
网格引脚阵列上路由网络的定义如下:
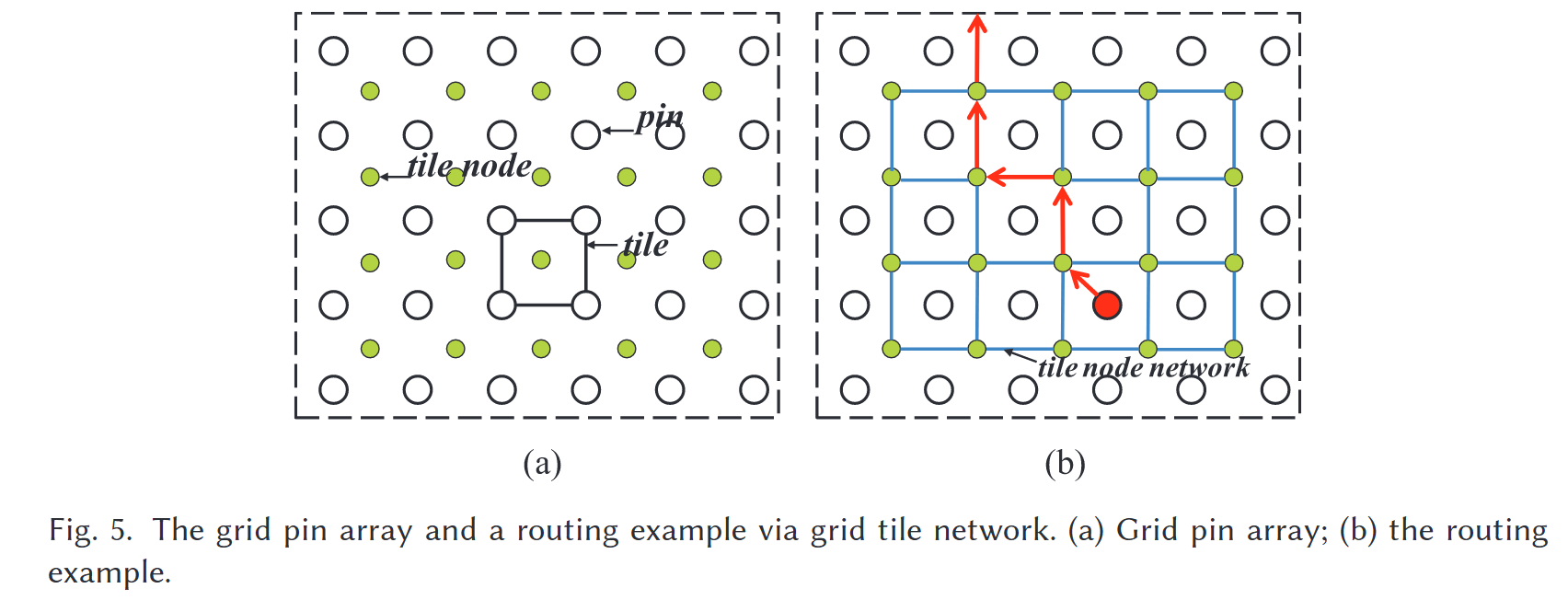
定义2.1(栅格引脚阵列):m×n栅格引脚阵列(GPA)由m行和n列组成。m×n引脚“排列”在一系列正方形的“网格”中。换句话说,每行和每列引脚都是对齐的。方形瓦片由四个相邻的引脚组成,我们假设每个瓦片的中心都有一个瓦片节点,如图5(A)所示。
定义2.2(网格平铺网络):相邻的瓦片节点可以相互连接以形成瓦片网络,如图5(b)所示。瓦片网络的边缘是逃生路由的通道。图5(b)举例说明了通过tile网络进行路由的示例。
虚拟节点就是瓦片节点,虚拟节点形成的网络就是路由路径。
对于网格引脚阵列上的有序逃逸布线,可以将问题转化为在容量、有序和不交叉的约束下,通过网格瓦片网络将多个商品从特殊引脚同时运送到引脚阵列边界。
2.3 SPA封装
为了适应PCB上引脚密度的增加,提出了交错引脚阵列。许多类型的交错引脚阵列可用于工业PCB设计。在本文中,我们考虑定义如下的类型:
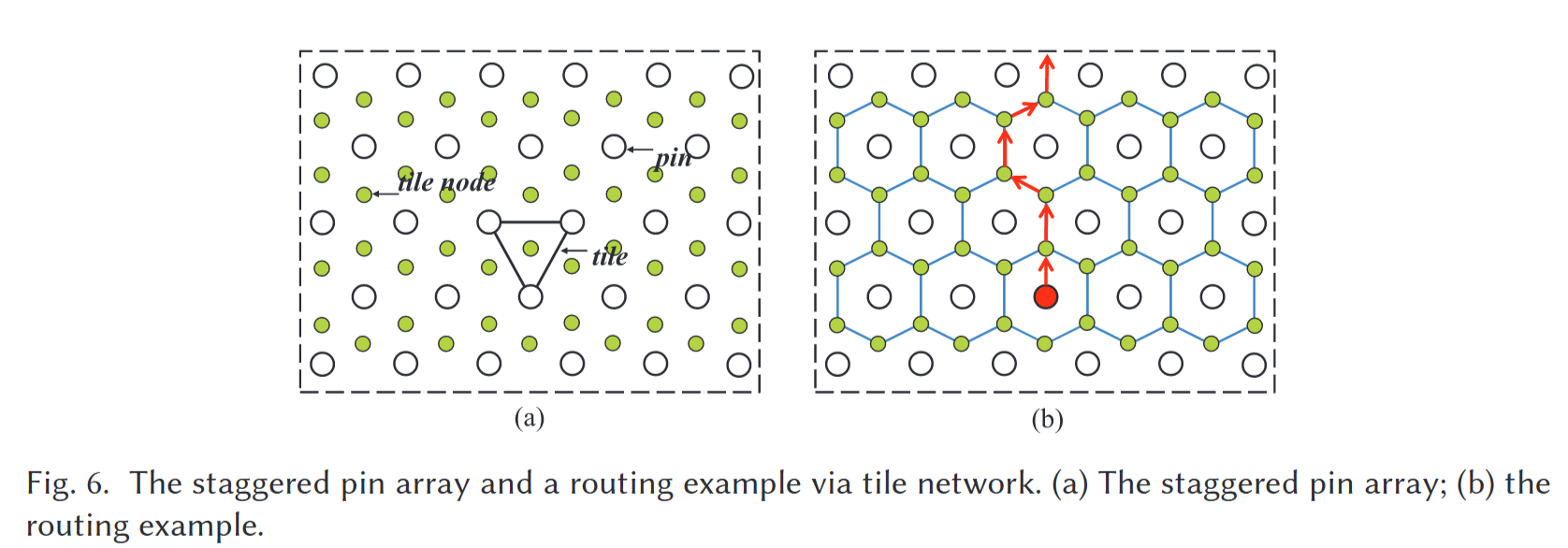
定义2.3(交错引脚阵列):m×n交错引脚阵列具有m行。每个奇数行有n个引脚,每个偶数行有n−1个引脚。连接任何相邻两个引脚的线之间的角度总是60度的倍数(Wang等人,2013)。三角形瓦片表示由三个相邻引脚形成的三角形区域,每个瓦片的中心都有一个瓦片节点,如图6(A)所示。
定义2.4(交错平铺网络):相邻的瓦片节点可以以六边形的形式相互连接,形成交错的瓦片网络,如图6(b)所示。交错瓦片网络的边缘是逃生路由的通道。图6(b)显示了通过交错瓦片网络进行路由的示例。
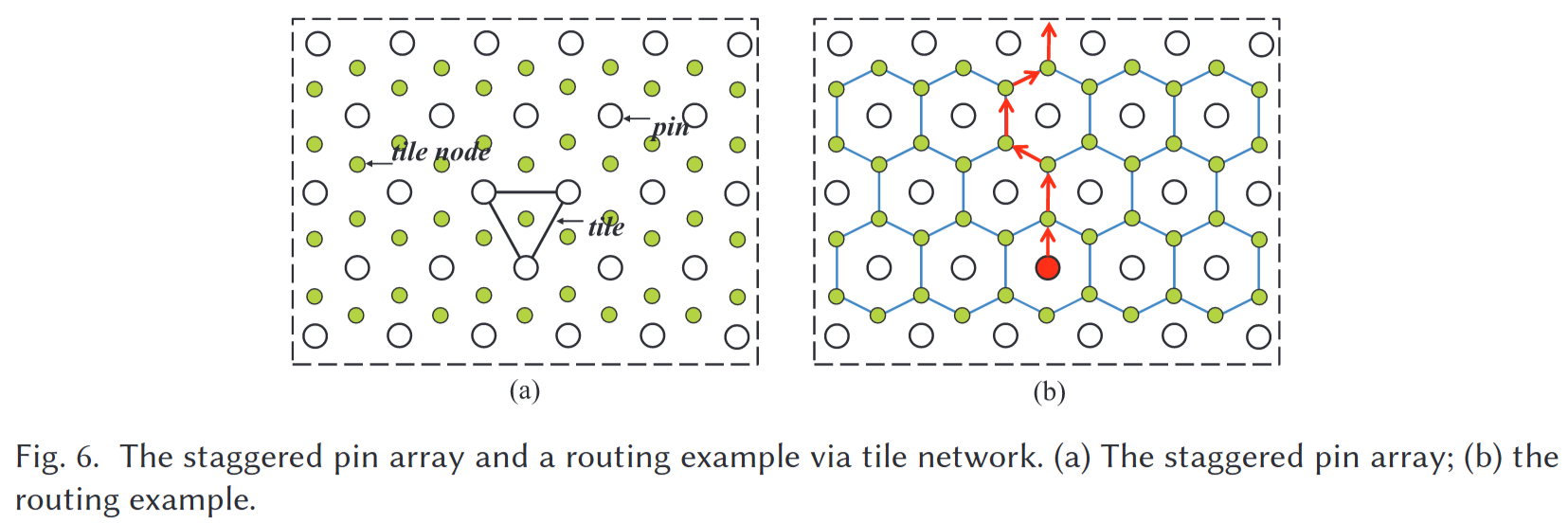
虚拟节点构成的网络不是四边形,而是正六边形。
3.PROBLEM FORMULATION
给定具有一组引脚 $P=\{P_1,P_2,\cdots,P_r\}$ 的m×n网格引脚阵列。将引脚布线到边界,不得交叉和超过每个信号路径的容量。此外,边界周围的逃逸布线需要遵循一些排序约束。同时,在100%的可布线性保证下,总导线长度需要最小化。
直观地说,输入是一个m×n网格引脚阵列,输出是满足三个约束的路由结果:非交叉约束、容量约束和排序约束。非交叉约束保证信号没有交叉。容量限制确保相邻引脚之间的信号总量不会超过容量。顺序约束意味着引脚不能按错误的顺序布线到边界。在不失一般性的情况下,我们可以假设目的地的顺序是1、2、3、,。。。,顺时针方向 $r$ ,其中 $r$ 是引脚数量,如果需要,可以适当地重命名引脚。
如果所有逃逸网的目的地都需要在引脚阵列的单侧逃逸,那么有序逃逸路由问题可以定义为单侧有序逃逸路由。类似地,我们可以定义双侧、三侧和四边的有序转义路由问题。
在给定差分对保护和线路长度匹配的约束下,问题变成了差分对有序逃逸路由。对于阻塞问题,只需添加阻塞区域的约束,即可避免信号通过。在引脚阵列中,容量包括正交容量和对角线容量(Yan和Wong,2012)。在本文中,为了简化问题,我们假设除了差分对路由之外,正交容量为1(O-cap),对角容量为2(D-cap)。
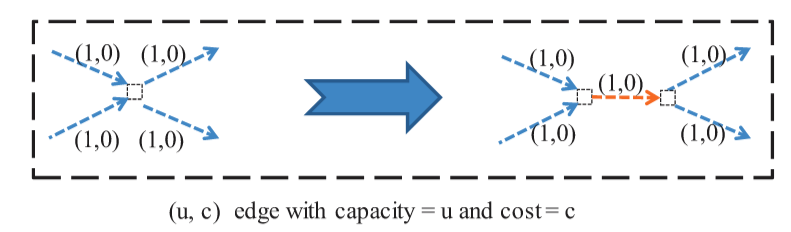
在引脚阵列中,设计规则限制两个正交或对角相邻引脚之间的导线数量。我们将这种约束分别称为正交容量和对角容量,简称为O-cap和D-cap(见图1)。如果我们考虑引脚阵列的瓦片,它是由四个相邻引脚形成的正方形,我们可以看到O-cap限制了通过其四边的导线数量,而D-cap限制了穿过其两条对角线的导线数量。
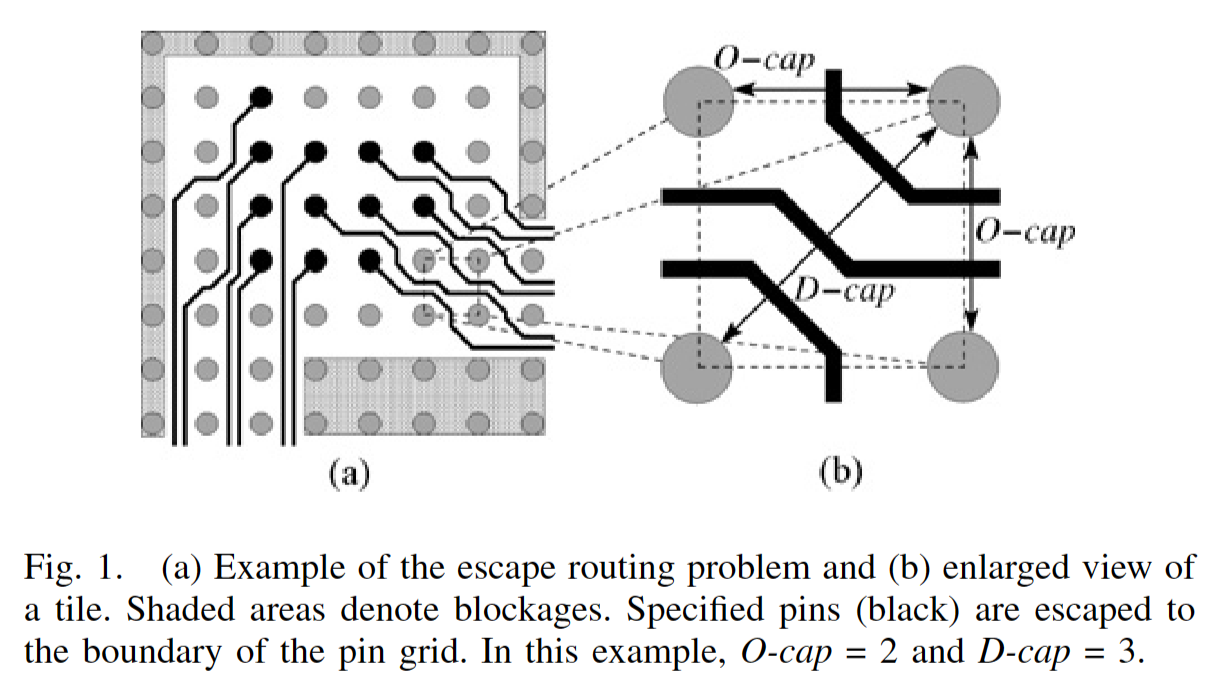
(a) 逃逸布线问题的示例和(b)瓦片的放大视图。阴影区域表示堵塞。指定的节点(黑色)将逃逸到节点栅格的边界。在本例中,O-cap=2,D-cap=3。
4 MMCF模型
在本节中,我们提出了最小成本多商品流模型(MMCF模型)来制定有序逃生路线,然后我们提出了三种满足约束的转换。构建最小成本多商品模型的概述流程如图所示。
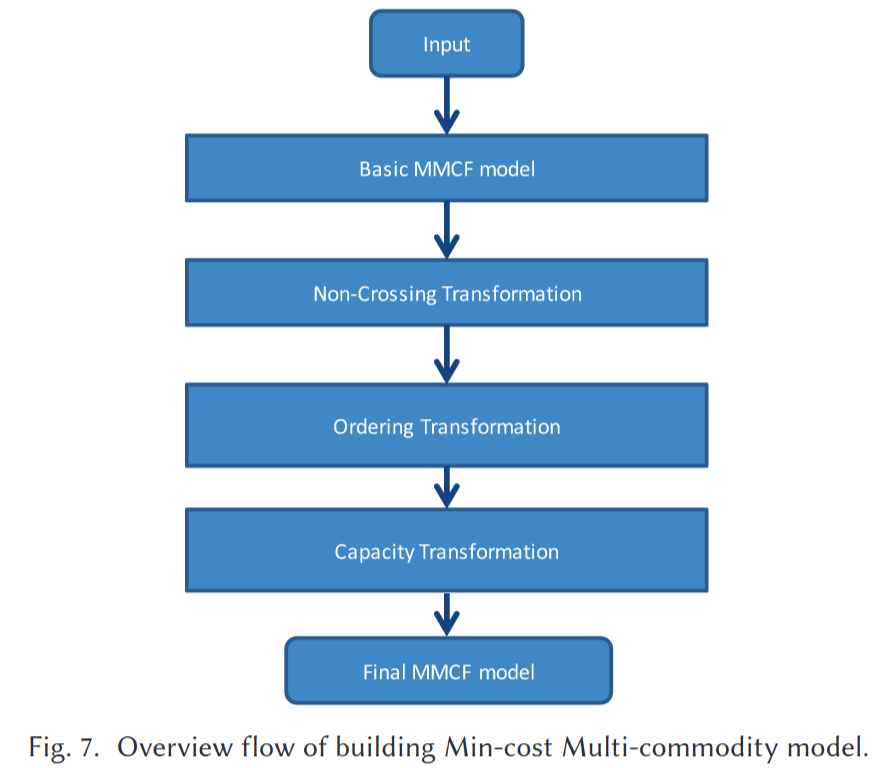
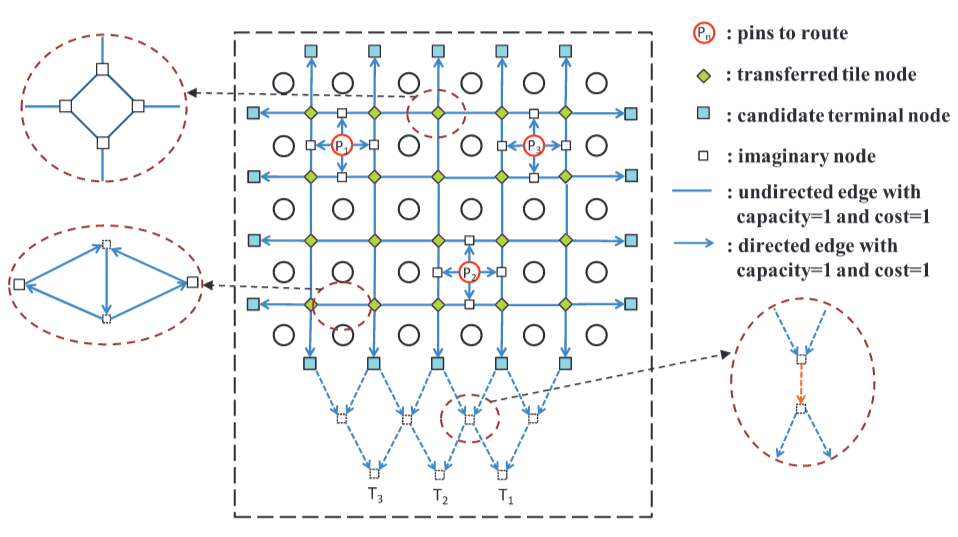
图8展示了基本的MMCF模型。我们在边界处放置额外的单元,称为候选终端节点。每个要布线的引脚都是模型中的源节点,它将向边界运送1个单位的商品。请注意,这些针脚运送不同类型的商品。选择相同数量的终端节点作为候选终端节点的运输目的地,同时满足顺时针的排序约束(在这个例子中,我们选择 $T1,T2,T3$ )。每条边的容量和成本为 $1$ 。 最后,我们得到一个MMCF问题,并且总线长等于问题的总成本。
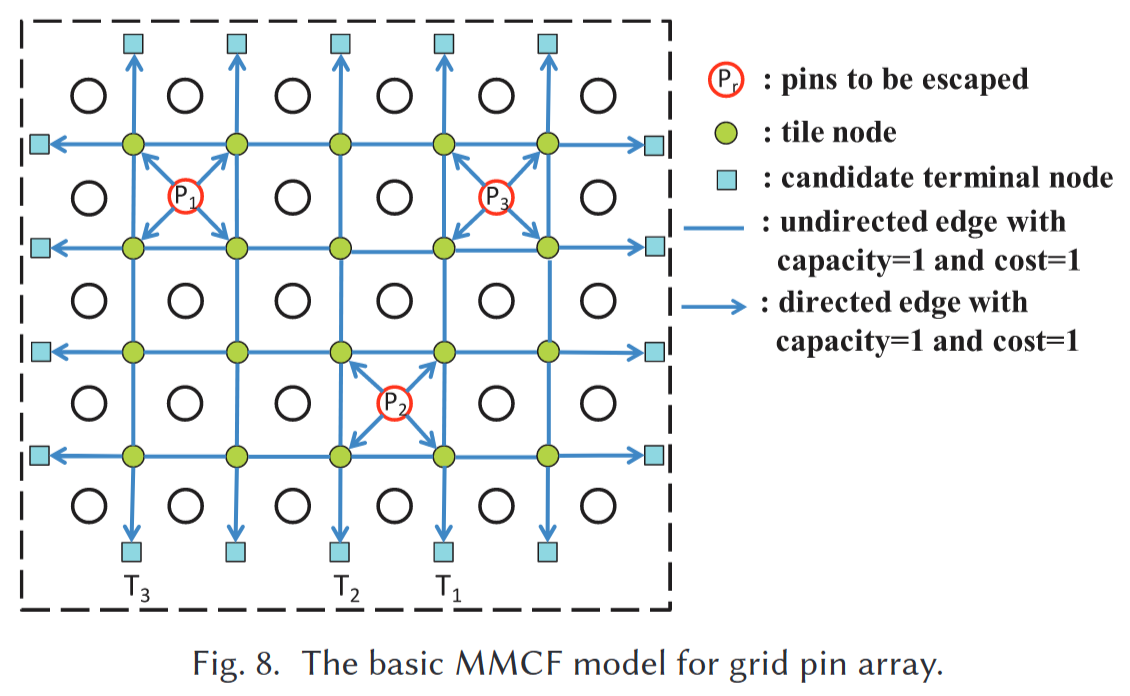
然而,模型中存在一些错误。首先,路由路径用于在PCB上传输信号,但两个信号的网络可能在瓦片节点处交叉。我们使用非交叉变换来避免它。第二,从终端节点中选择目的地的组合太多。如何确定具有正确排序约束的目的地是一个大问题。我们使用排序变换来求解。第三,网络中既有无向边,也有向边,在使用MMCF求解器求解之前必须统一。但是,当我们将无向边转换为有向边时,要满足容量约束有点困难,这将用于容量转换。为避免错误而进行的转换的详细信息将在以下部分中介绍。
4.1 非交叉约束建模
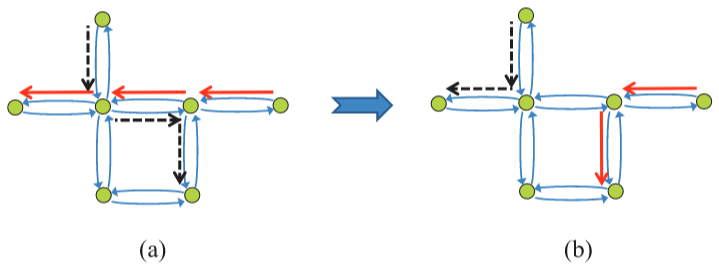
如图10(a)所示,两个信号的网络可以在瓦片节点处交叉。在无序转义路由中,通过交换交叉节点后的路径可以很容易地解决这个问题,如图10(b)和10(c)所示。然而,在有序转义路由中要避免交叉要困难得多,因为不允许交换路径,这不符合排序约束。
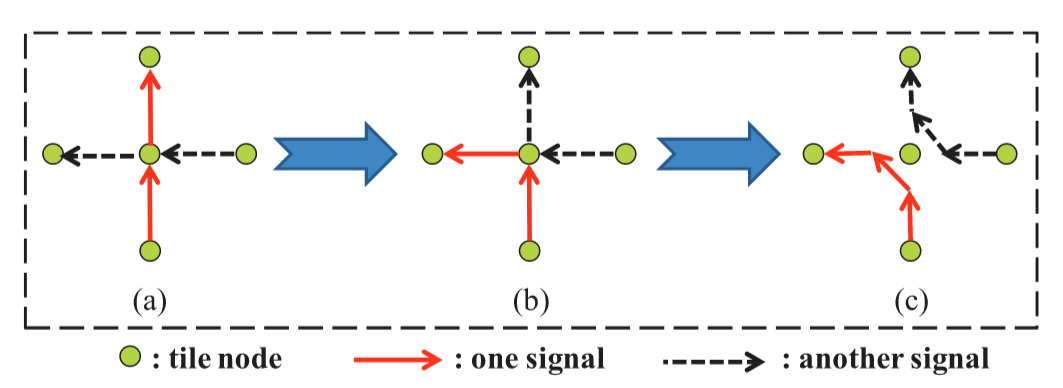
首先,我们列举了网格引脚阵列(如图11所示)和交错引脚阵列(图12所示)中所有可能的交叉情况。之后,我们定义了两种类型的交叉,如下所示:
定义4.1(第一类交叉):类型1交叉是来自两个瓦片节点的信号之间的交叉,如图11(a)所示
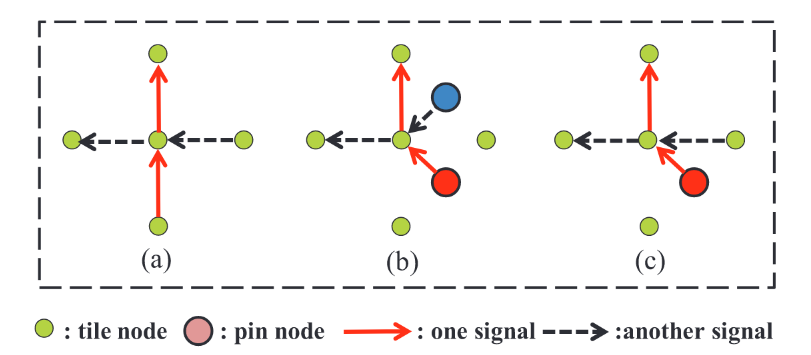
定义4.2(第二类交叉):2型交叉是来自两个引脚的信号之间的交叉(图11(b)),或来自一个引脚和一个瓦片节点的信号之间(图11的(c))。
请注意,第一类交叉仅存在于栅格引脚阵列中,因为交错引脚阵列中没有交叉瓦片节点。
4.1.1 建模第一类交叉
为了避免类型1交叉,我们必须将基本瓦片模型转移到新的瓦片模型,如下所示:
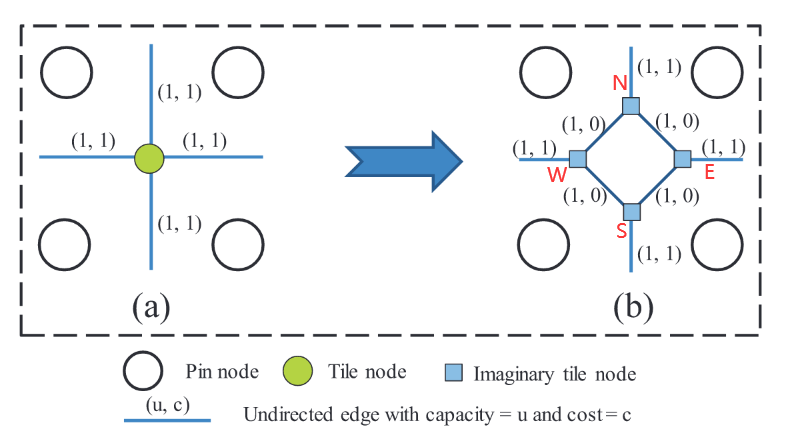
定义4.3(非交叉变换类型1):对于每个瓦片,创建四个虚拟瓦片节点,分别是N-瓦片、E-瓦片、S-瓦片和W-瓦片(见图13(b))。在分别具有容量1和成本0的节点对(N,E)、(E,S)、(S,W)、(W,N)之间创建无向,将这样的边称为瓦片内边。N-tilenode与北邻的S-tilenode以无向边连接,其容量和成本为1。将这样的边称为瓦片间边。其他三个虚拟瓦片节点也连接到具有瓦片边的相邻节点。
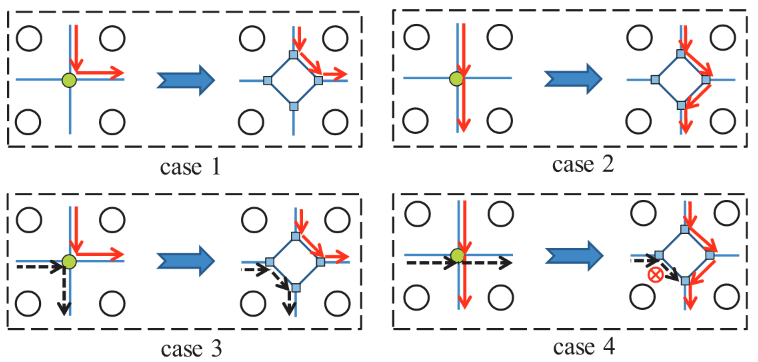
注意边的容量的限制。case 4中因为一条边需要走两个相邻的虚拟边,存在重叠,但是容量为1,因此出现矛盾。
4.1.2 建模第二类交叉
2型交叉是由引脚节点引起的。对于栅格引脚阵列,避免它们的转换如下:
定义4.5(GPA非交叉变换类型2):对于要转义的每个引脚,在引脚周围的四条边的中心创建四个虚拟引脚节点,分别为N-引脚节点、E-引脚节点、S-引脚节点和W-引脚节点(见图15(b))。假想的pin节点将边划分为八条边,这些边被称为 around-box 的边。在引脚节点和虚拟引脚节点之间创建有向边,容量为1,成本为0。将这些边称为 in-box 边。
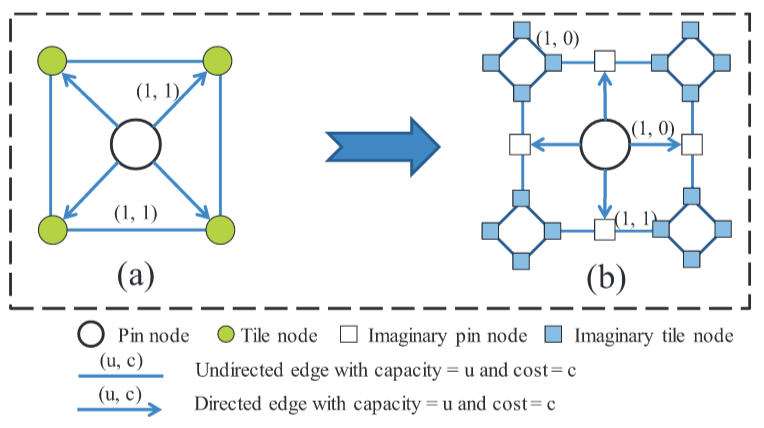
4.2 排序约束建模
在有序转义路由中,引脚必须转义到具有排序约束的引脚阵列的边界。然而,我们不必在一开始就确定它们的目的地。但在MMCF问题中,我们必须首先选择每种商品的目的地。
一个可行的解决方案是枚举满足排序约束的所有终端组合。之后,解决每一个案例并选择最佳结果。对于 $m×n$ 栅格引脚阵列,有 $2m+2n−4个$ 候选端子。如果我们有 $r$ 个引脚要转义,那么合法组合的总数是 $C_{2m + 2n - 4}^r$ 。然而,该方法效率低下,我们更倾向于在统一的最小成本最大商品流模型中解决问题。
用正确排序决定每个商品目的地的方法的定义如下:
定义4.8(有序变换):假设有 $r$ 个引脚和 $k(k\ge r)$ 个候选终端(见图17第1行)。创建 $k-r$ 行的假想终端节点,并且下一行的节点数比上一行少一个。换句话说,每行的节点数形成一个公差为1的算术级数。注意,最后一行的节点数是 $r$ ,等于要布线的引脚数。让 $T_{i,j}$ 表示第 $i$ 行的第 $j$ 个节点。在第 $i$ 行的节点对 $(T_{i,j} ,T_{i +1,j})$ 和 $(T_{i,j+1},T_{i +1,j})$ 之间建立有向边,如图17所示。每条边的容量为1,成本为0。最后一行的虚数节点是要逃逸的引脚的终端。把这些节点称为目的节点。换句话说,目标节点是我们MMCF模型的目的地。
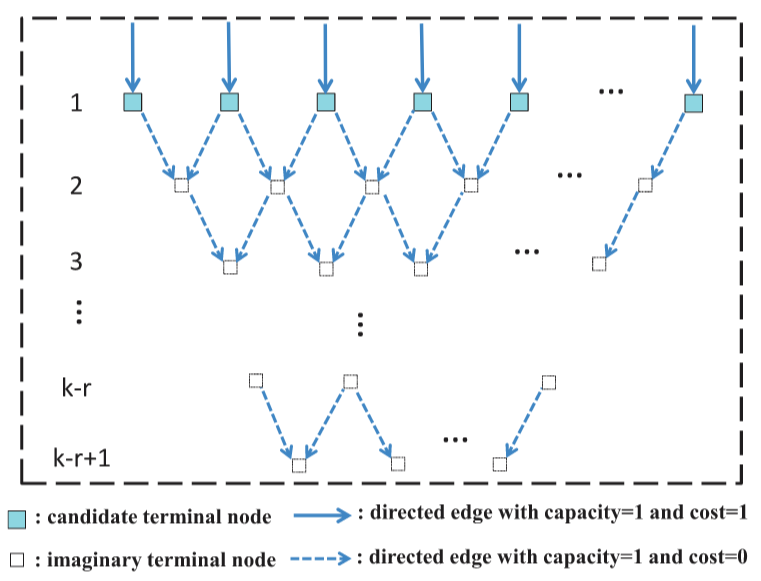
为了保证排序约束,在我们的网络模型中,最多只有1个信号可以通过每个虚构的终端节点。为此,我们可以用一条假想的边代替假想的终端节点(最后一行除外),其容量为1,成本为0,如图18所示。
如果所有要转义的引脚都以正确的顺序路由到边界,那么让我们称转义路由是合法的。如果所有来自源节点的商品都被传输到正确的目的地节点,那么我们的MMCF流是合法的。定理3保证了这两个合法性的等价性。
4.3 容量约束建模
如上所述,在本文中,我们只考虑每条边的容量为1。因此,只有当多商品流是一个整体流时,我们才能确保流量解决方案对应于一个有效的路由解决方案。然而,在MMCF模型中既有有向边,也有无向边。容量为1的无向边意味着只有一个单位的商品可以在这条边上进行转换,其方向可以是前向和后向。在用MMCF求解器解决网络模型之前,我们必须将无向边转换成有向边。
在无序逃逸路由中,创建一条前向边和一条后向边来替代容量相同的无向边u,如图20(a)所示。如果一个信号占据了前向边,另一个信号占据了后向边,那么原来的无向边的容量就被超过了。幸运的是,我们可以把前向边和后向边的信号都去掉,然后交换路径,就可以轻松解决问题,如图21(a)所示。然而,在有序逃逸路由中,该方法是非法的,因为它不能满足排序约束。解决该问题的转换方法如下(Ahuja等人,1993)。
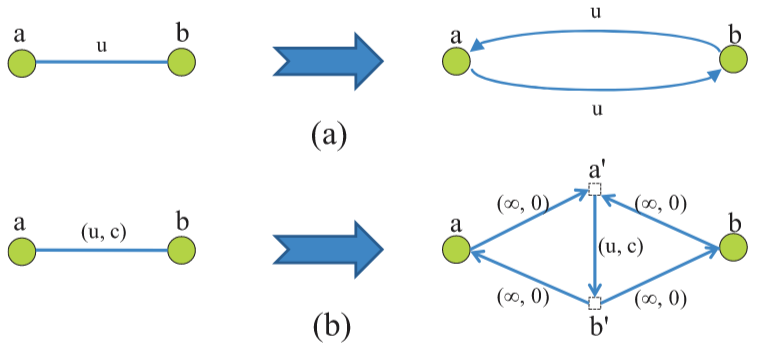
定义4.12(容量转换):
对于每条无向边,创建两个假想的节点。然后,创建一条容量为u、成本为c的有向边来连接它们。之后,创建四条容量为 $\infty$ 、成本为0的有向边来连接相邻的节点,如图20(b)所示。
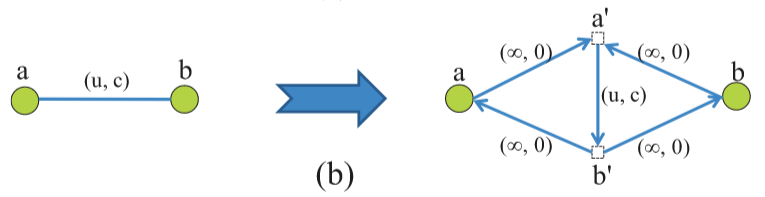
无向网络中节点a和节点b之间的每一个流动单位必须在有向图中的路径a-a′-b′-b或b-a′-b′-a上流动。弧(a′,b′)意味着这种流动不能超过u。此外,每个单位产生的费用为c。通过第4.1, 4.2, 4.3节介绍的转换,我们将基本的MMCF模型转换为最终的MMCF模型,如图22和23所示,正确捕捉了有序逃逸路由中的约束。
5.DIFFERENTIAL PAIR PROCESSING
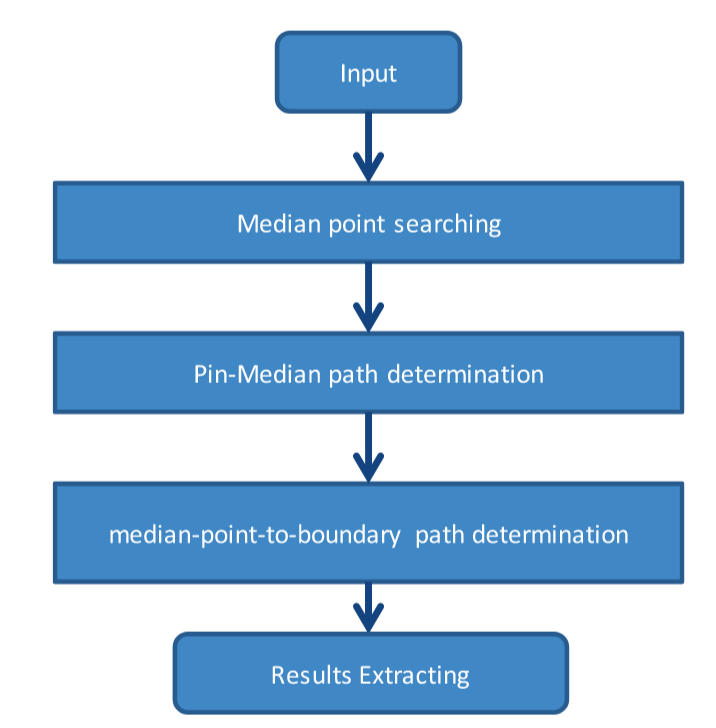
差分对处理的概述流程如图24所示。它基于Wang等人提出的算法。(2014)。由于篇幅有限,我们只会说明Wang等人(2014)和我们的方法之间的不同方面。
- 选择中间点,也就是汇聚点
- 逃逸引脚到中间点的路径选择
- 确定中间点到边界的路线
- 结果提取
5.1 中间点搜索算法
第一步是找到所有的中位点。一个差分对的最小成本中位点是一个具有最短和相等的曼哈顿距离的点。有人提出了一种有效的方法,为每个差分对找到基于GPA的中位点候选人(Li等人,2012)。同样地,Wang等人(2014)提出了基于SPA的算法。通过列举所有差分对位置的情况,我们可以得到所有的中值点。如图25和26所示。
5.2 引脚中间点路径确定
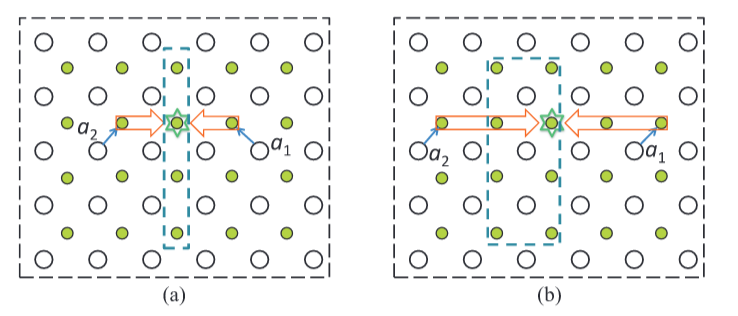
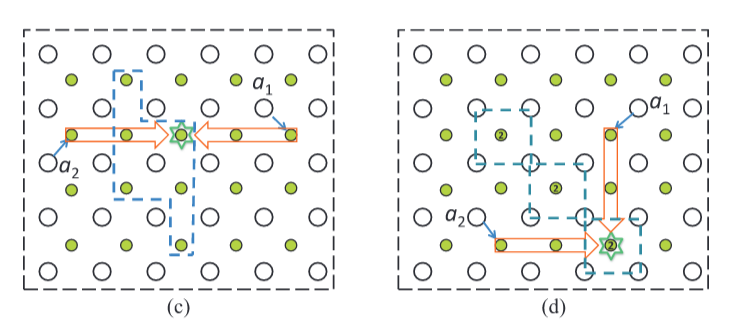
基于上述情况,我们可以计算出每个差分对的所有中值点候选者。下一步是获得从引脚到中位点的所有可能路径。由于这些路径占用了路由资源,我们最好得到最短的引脚-中位点路径。
以GPA为例,我们可以通过枚举法获得所有最短的引脚-中点路径,如图27所示。但是,在有序逃逸路由中,有些路径对于排序约束来说是非法的。假设差分对的排序是边界处顺时针方向的a1,a2。对于图27中的情况d,a1和a2在中间点汇合后,它们可以向东走或向北走,通过瓦片网络到达边界。无论他们选择哪个方向,他们都会以错误的顺序到达边界。对于情况a、情况e、情况f和情况g,在中位点收敛后只有一个方向是正确的,对于情况b、情况c、情况d、情况h和情况i,两个方向是正确的。
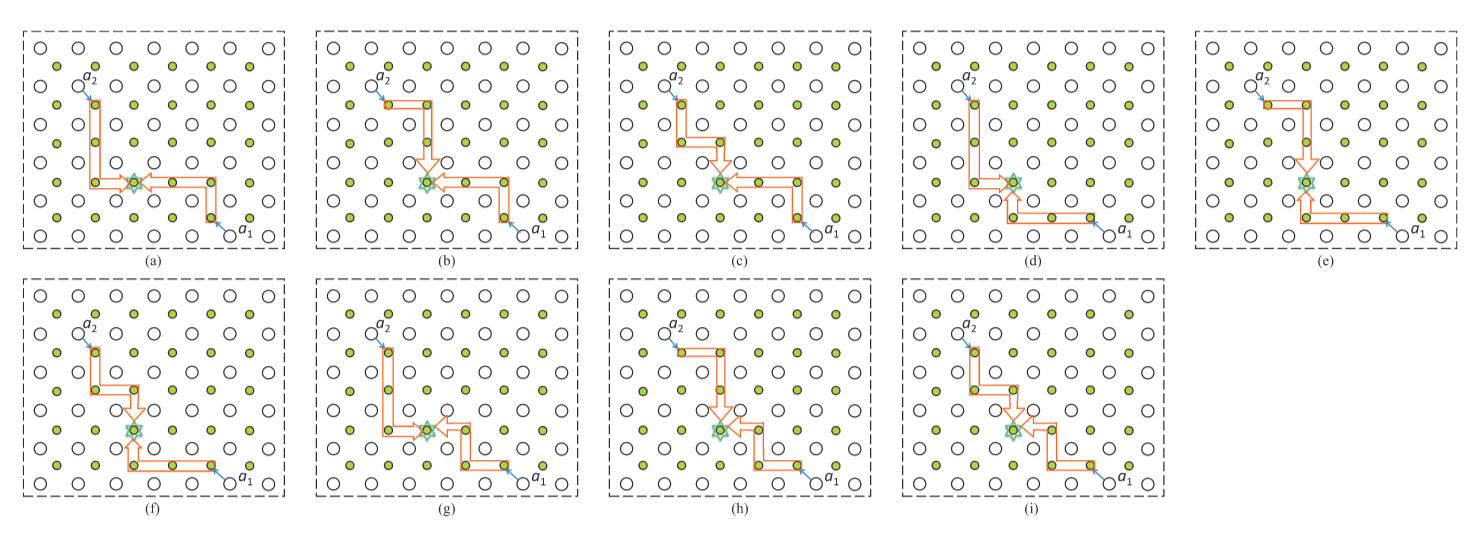
5.3 中间点到边界路径的确定
在为每个差分对枚举所有合法的最短引脚中点路径之后,下一步是确定要使用的路径。与Wang等人(2014)类似的基于ILP的方法可以应用于求解,不同之处在于我们考虑了排序约束的合法方向数的权重。然后,使用MMCF模型将中间点布线到边界,如图28所示。请注意,在确定引脚中点路径后,具有错误排序的方向的容量将设置为0。
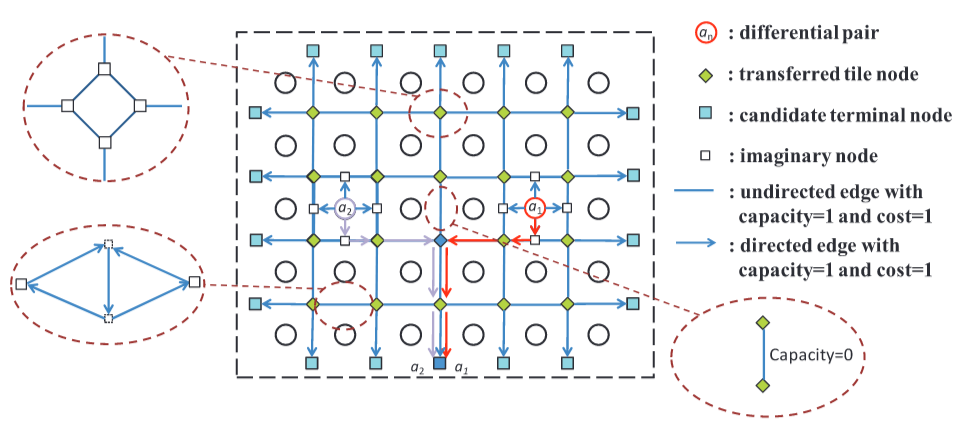
6.BLOCKAGE-AVOIDED PROCESSING(避开阻塞区域的处理)
如上所述,具有过度热变化或其他应用的区域不能传输信号。在我们研究如何处理这些区域之前,首先定义阻塞边界:
定义6.1(区块边界):区块边界由区块网络的某些边组成。它包含了面积最小的整个堵塞物。
我们提出了一种获得阻塞边界的方法,如图30所示。具体来说,计算堵塞物占用的瓷砖。这些瓦片形成一个多边形,多边形的边界就是阻塞边界。
在获得阻塞边界后,我们可以去除所有的内部边,并使用MMCF模型来处理该问题。请注意,不会删除阻塞边界的边缘。