A Unified Printed Circuit Board Routing Algorithm With Complicated Constraints and Differential Pairs

Ting-Chou Lin, Devon Merrill, Yen-Yi Wu, Chester Holtz and Chung-Kuan Cheng
UC San Diego, La Jolla, CA, USA
{til002, djmerril, yew001, chholtz, ckcheng}@eng.ucsd.edu

Aspdac 21: Asia & South Pacific Design Automation Conference

亚洲及南太平洋设计自动化会议

The-OpenROAD-Project/PcbRouter (github.com)

The-OpenROAD-Project/KicadParser (github.com)

摘要

印刷电路板（PCB）布线问题近年来得到了广泛的研究。由于不断增长的净/引脚数、极高的引脚密度和独特的物理限制，PCB的人工布线已成为实现设计闭合的耗时任务。以前的工作将问题分解为逃逸布线和区域布线，并分别关注这些问题。然而，这两个问题之间总是存在差距，需要大量的人力来来回微调算法。此外，先前的区域路由工作主要集中在逃逸路由球栅阵列（BGA）封装之间的路由。然而，在实践中，许多组件不是BGA封装的形式，例如无源器件、去耦电容器和通孔引脚阵列。为了缓解先前工作的不足，我们提出了一种完整的电路板布线算法，该算法可以处理多个现实世界中的复杂约束，以促进印刷电路板布线并产生高质量的可制造布局。实验结果表明，该算法是有效的。具体来说，对于所有给定的测试用例，我们的路由器可以实现100%的可路由性，而不会违反任何设计规则，而其他两个最先进的路由器无法完成某些测试用例的路由，并导致违反设计规则。

INTRODUCTION

近年来，由于网络/引脚数量的增长、极高的引脚密度和特殊的物理限制，印刷电路板（PCB）的手动布线已成为一项耗时的任务。此外，高性能PCB所需的物理约束，如长度匹配布线、成对布线和平面布线，仍然是PCB布线自动化的负担[1，2]。此外，对于高性能PCB设计，高频信号传输通常通过差分对[3]。差分对具有几个优异的特性，如更好的接地偏移耐受性、更高的抗干扰性和更好的电磁干扰降低，使其成为高性能PCB设计的流行技术。为了实现差分对的优点，每个差分对中的两个连接应以匹配的线长度彼此靠近地布线，从而导致差分对布线不平凡。

差分对布线

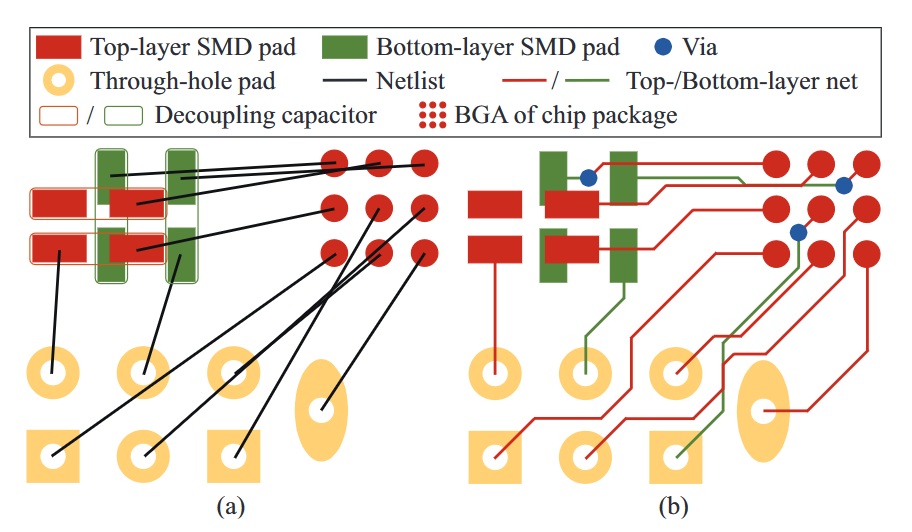
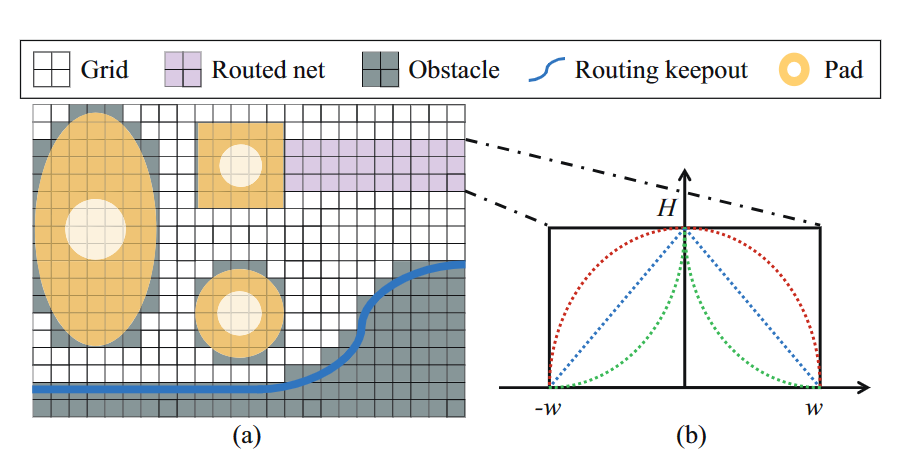
此外，由于简化的原因，以前的PCB布线工作通常考虑的是芯片封装的常规球栅阵列（BGA）之间的连接[1]。然而，从我们对实际PCB设计的观察来看，设计中包含很多不是BGA封装的元件，如无源器件、去耦电容、通孔引脚阵列等，是很常见的。图1(a)显示了一个部分实际PCB设计的例子，其中有BGA封装以外的元件。这些非BGA封装的元件通常不规则地分布在PCB设计内部，这就造成了布线拥堵的不均匀分布，使布线任务更加困难。因此，开发一种能够处理此类设计的PCB布线算法，同时满足高性能PCB的独特物理约束，是非常可取的。

1.1先前的工作

广泛研究的PCB布线问题的目标是在满足各种物理约束的同时，布线芯片封装的BGA之间的所有连接。此外，通孔的使用通常受到限制，因此布线变得平坦。这种平面布线方式使PCB布线成为与IC布线不同的问题。先前的研究将PCB布线问题分为两类：

（1）逃逸布线问题：从BGA的焊盘路由到它们的阵列边界。

（2）区域布线问题[1，2]。区域布线问题是连接BGA的先前逃逸路线，通常受制于每个连接的布线长度上限/下限。

逃逸布线和区域布线

工作[4-10]集中讨论了逃逸路由问题。逃逸路由问题可以进一步分为无序逃逸和有序逃逸；前者需要不对边界上的连接进行特定排序的路由，而后者则需要。Wang等人[4]提出了一个三角形模式和序列的模型，以促进基于网络流的方法，得出无序逃逸路由解决方案。Kubo等人[5]开发了一种迭代的通道分配方法，以有效地减少线路拥堵和总线长。Fang等人[6, 7, 9]也利用了基于网络流的算法来进行无序逃逸路由。Fang等人[8]提出了一种基于整数线性编程的方法，并采用了减少技术 在合理的运行时间内完成有序逃逸路由。Yan等人[10]提出了一个能够正确反映路由资源能力的网络模型，从而得到了一个更好的无序路由的结果。

逃逸布线：

• 有序逃逸：需要按照顺序
• 无序逃逸：无序按照顺序对连接布线

工作[11-14]解决了具有长度匹配约束的区域路由问题。Ozdal等人[11]采用了基于拉格朗日松弛的路由方案来获得长度匹配的路由解决方案。此外，Ozdal等人[12]提出了一种有效的river-routing-based的算法，以解决channel内的长度匹配路由问题，其理论上的恒定系数为最佳解。Yan等人[13]提出了一种基于有界切片线网格的算法，以在没有任何路由拓扑限制的情况下检索路由解决方案。Yan等人[14]基于路由区域划分和最大流量算法建立了障碍感知路由框架。

主要讲区域路由

除了传统的逃逸路由和区域路由问题，工作[15–21]在考虑差分对约束的同时处理路由问题。Fang等人[16，18]提出了一种考虑差分对的芯片封装板代码设计算法，但他们对单调路由的假设限制了该算法的实际使用。Yan等人[17]提出了一种考虑路由拥塞的基于协商的路由算法，以完成差分对的路由。Li等人[19]采用了两阶段方案和最小成本最大流量算法来同时路由所有差分对。Wang和Jiao等人[20，21]在考虑差分对的情况下，开发了交错引脚阵列的无序和有序逃逸路由算法。

差分对约束布线问题

1.2 前人工作的区别

如上所述，我们注意到PCB设计中存在非BGA封装的不规则性。对逃逸布线和区域布线的传统研究可能不适合处理这些不规则性，因为它们假设PCB设计仅包含BGA封装。因此，有必要有一种新的统一算法来处理这类路由问题。

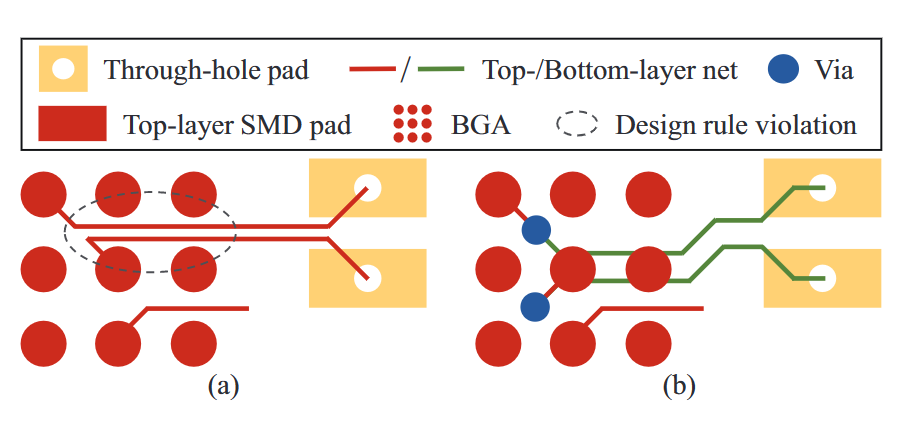
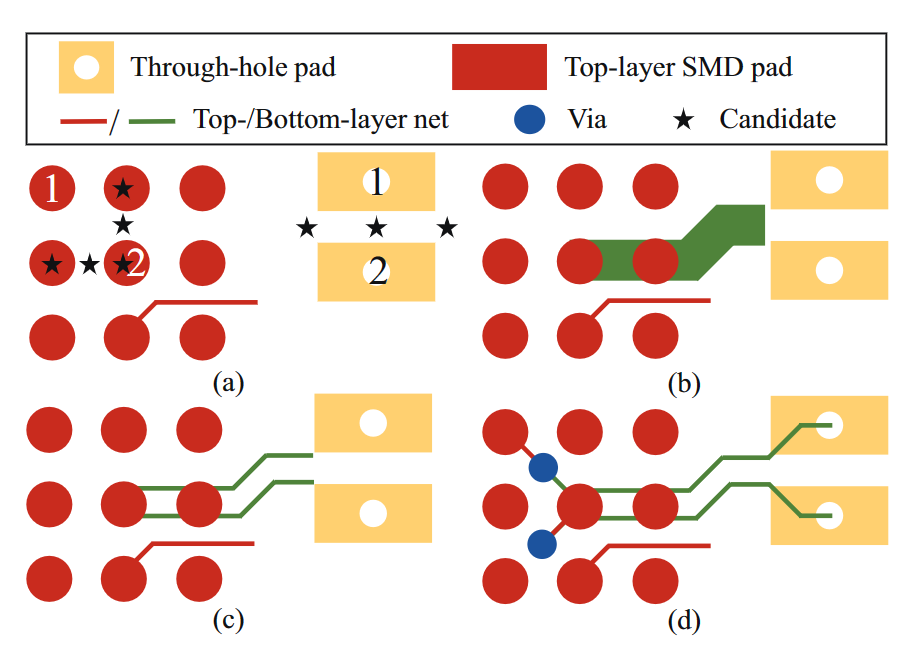
图1（a）和（b）分别显示了该路由问题的示例和（a）中的可行路由解决方案。从这个例子中，很明显，由于非BGA封装的不均匀分布，逃逸路由和区域路由的组合不适合处理此类路由问题。此外，我们观察到，差分对的路由与之前的工作中假设的问题不同。由于封装具有非常密集的BGA，差分对的两个网络可能没有足够的空间通过同一层上的非常密集BGA。因此，在这种非常密集的BGA上执行逃逸路由的唯一可行方法是在BGA的焊盘之间分配一个“狗骨”通路，然后在不同的路由层上逃逸网络。图2（a）显示了工作[21]提供的一种可能的路由解决方案。由于BGA之间的空间有限，该解决方案遭受各种设计规则冲突，因此不是优选的。因此，需要提出一种新的路由算法，该算法可以处理具有非常密集BGA的差分对路由。图2（b）显示了我们提出的算法的路由结果，其中分配了“狗骨”通孔，差分对通过不同的路由层逃逸。

表面贴装器件SMD（Surface Mount Device）封装是将电子元器件直接贴在基板上，即将芯片组件封装并放置在印刷电路板上，利用回流炉熔化电子系统互连的焊锡合金，从而实现芯片组件与基片互连的主要技术。

SMD（Solder-Mask Defined Pad Design，防焊限定焊垫设计）就是使用solder-mask(绿漆/绿油)覆盖于较大面积的铜箔上，然后在绿漆的开口处(绿漆没有覆盖)的地方裸露出铜箔来形成焊垫(pad)的称谓。因为这种焊垫的尺寸会取决于绿油开孔的大小，所以才会说是防焊限定焊垫。

图1：（a）典型PCB布线布局的局部视图，包括SMD焊盘、通孔焊盘和网表。注意，SMD焊盘出现在顶层或底层，而通孔焊盘从上到下贯穿所有层。（b） 来自（A）的给定PCB布线布局的可行布线结果。

图2：先前工作[21]的扩展与我们的算法之间的比较。（a） 工作[21]的扩展提供了一种可能的路由解决方案，其中由于BGA之间的空间有限，引入了设计规则冲突（即间距冲突）。（b） 由我们提出的算法提供的布线结果，其中分配了“狗骨”通孔，差分对通过不同的布线层逃逸，以避免间距冲突。

1.3 本文贡献

我们将主要贡献总结如下：

• 以前的大多数工作都有一个假设，即PCB设计是用常规的BGA，因此他们可以通过逃逸路由和区域路由的组合来处理PCB的路由。然而，在现实中，很多PCB设计包含的封装并不是BGA，这使得以前的大多数工作不适用于此类设计。本文是文献中第一个提出全面的多层PCB布线算法的工作，该算法可以处理这类设计，在统一的布线框架下，将电源/地线、差分对和信号网一起进行布线。此外，还提出了一个新的路由网的障碍成本函数，以促进路由资源的协商。
• 我们提出了一种多层差分对路由方案。与以前的工作相比，之前的方法只能以单层路由方式处理差分对，因此我们的方法可以通过位置搜索更好的狗骨，并执行多层差分对路由。此外，我们提出的方案允许差分对与所有其他信号网络协商路由资源，以提高总体可路由性。
• 我们提出了一种焊盘入口感知后处理方法，该方法可以进一步完善我们的布线解决方案，以提高制造能力。通过修改衬垫间隙区域内的布线段或添加填充物，可以有效地消除锐角和间隙的设计规则冲突。
• 基于实际学术和工业PCB设计的实验结果表明，我们的算法是有效的。特别是，我们的路由器可以在所有测试用例中实现100%的可路由性，而不违反任何设计规则，而其他两个最先进的路由器在多个测试用例中无法完成路由，并导致违反设计规则，危及可制造性。

本文的其余部分组织如下。第2节阐述了所解决的问题，并阐述了PCB布线设计规则。第3节详细介绍了我们提出的算法。第4节显示了实验结果。第5节总结了本文。

PRELIMINARIES

在本节中，我们提供了PCB布线问题的正式定义，并描述了与我们的问题相对应的布线设计规则。

2.1 问题描述

在本文中，我们关注一个统一的多层PCB布线问题。我们首先提供本文中使用的以下术语和符号：

• 焊接掩模定义（SMD）焊盘：在网表中具有预定义分配的顶层或底层焊盘。
• 通孔焊盘（Through-hole pad）：在网表中具有预定义分配的所有布线层上打孔的焊盘。
• $ 𝑁 =\{𝑛_1,𝑛_2,\cdots,𝑛_𝑚\} $ 是网表，其中 $ 𝑚 $ 是网络的数量 $ 𝑛_𝑖 $ 定义SMD焊盘或通孔焊盘之间的连接。

图1（a）显示了考虑的PCB布线平面的部分结构示例。与之前的工作不同，布线平面周围散布着SMD焊盘和通孔焊盘，它们不是BGA。由于这些不规则性，先前工作提出的算法通常不适用于此类路由问题。图1（b）显示了满足所有设计规则的两层路由结果示例。这里，我们正式定义问题如下：

• 统一多层PCB布线问题：给定一组SMD焊盘、一组通孔焊盘、网络列表 $ 𝑁 $ , 一组设计规则，连接所有网络 $ 𝑛_𝑖\in 𝑁 $ 从而不存在违反设计规则的情况，并且使总导线长度最小化。

2.2 布线约束规则

在本文中，为了在保持更好的可制造性的同时降低设计复杂性，我们的算法应该处理几个路由设计规则。我们问题中的五个主要设计规则详细如下：

• 非交叉和间距约束：同一层上不允许净交叉。此外，同一层上的路由网络应保持彼此之间特定的间距。
• 布线角度约束：可以执行90度或135度的布线角度。但是，45度的布线角度是不允许的。
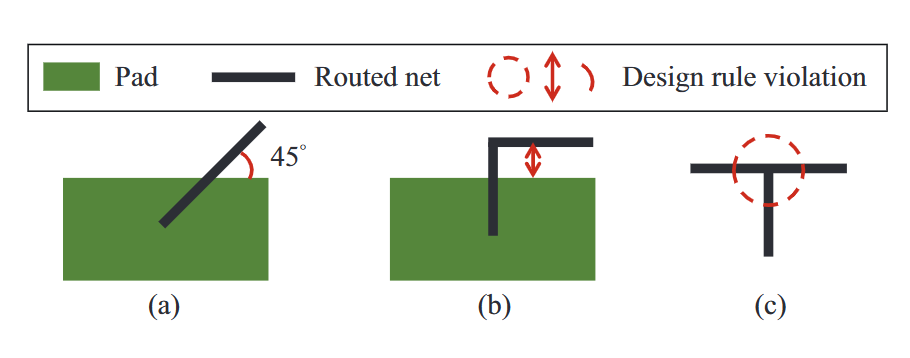
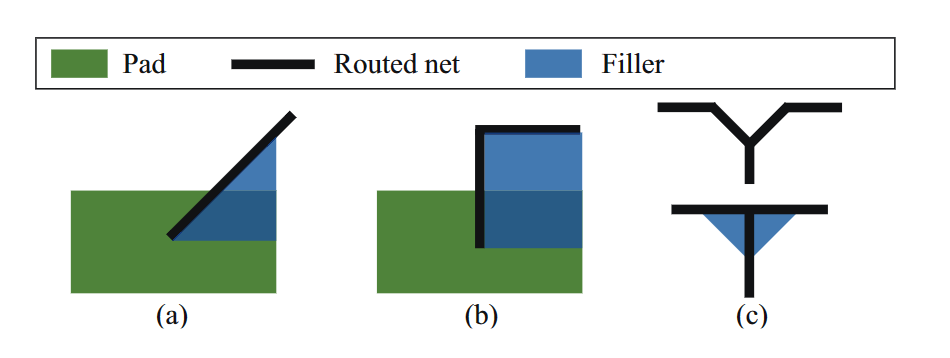
• 焊盘进入限制：进入焊盘的布线网络不应在彼此之间引入锐角；否则，称为锐角设计规则违反。此外，如果布线网络未进入焊盘，则应在布线网络和焊盘之间保持一定的间距；不管怎么说，它被称为间隙，一种违反设计规则的行为。图3（a）和（b）分别显示了锐角和间隙设计规则违规的示例。
• T形接头约束：在同一层上连接有三段的布线网络应保持Y形接头，而不是T形接头。图3（c）显示了违反T形接头设计规则的示例。
• 差分对约束：差分对的路由网络应尽可能接近彼此，且具有相似的路由线路长度。

图3：违反路由设计规则的示例。（a） 违反衬垫进入限制的锐角：布线网与衬垫之间的角度应为90度或135度。（b） 小间隙违反焊盘入口约束：布线网和焊盘之间的间距应大于指定值。（c） 违反T形接头约束：同一层上连接在一起的布线网络的三段应保持Y形接头，而不是T形接头。

ALGORITHMS

在本节中，我们将介绍我们的路由算法。首先，我们概述了我们提出的算法。然后，我们详细介绍了算法每个阶段使用的方法。

3.1 算法概述

图4总结了我们基于网格的布线算法，它包括三个主要阶段：

1. 考虑任意焊盘形状的布线网格初始化，
2. 迭代印刷电路板布线
3. 设计规则感知后处理。

在第一阶段，我们通过将障碍物和垫的任意形状光栅化到布线网格来捕获布线障碍物。第二阶段是迭代PCB布线。

图4：我们提出的算法的路由流程。

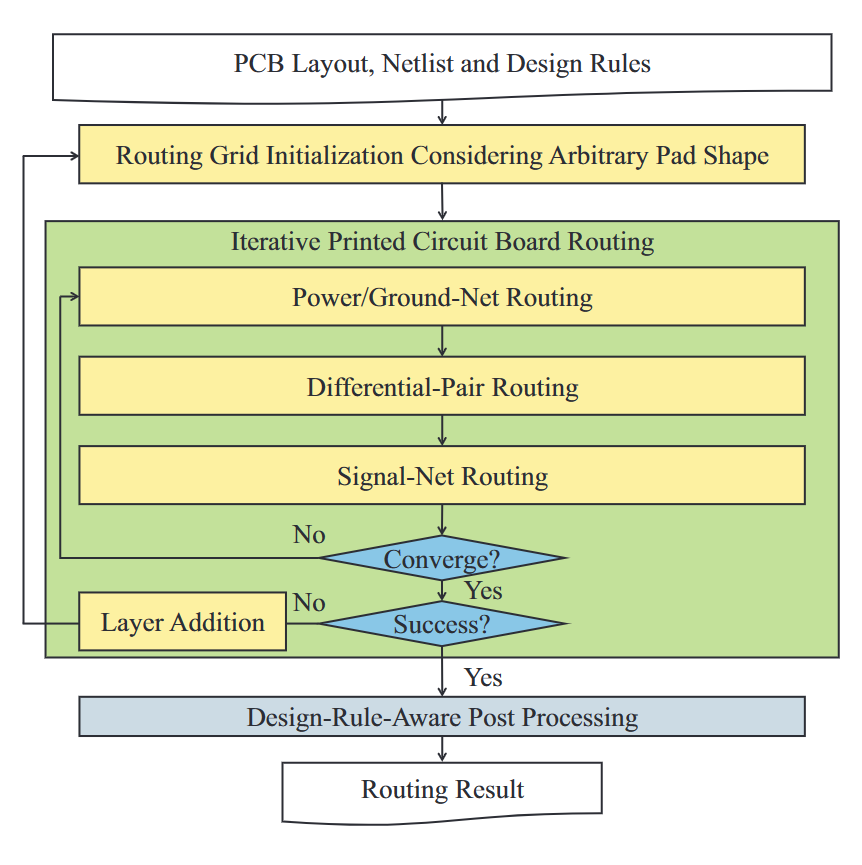
每次迭代包括电源/接地网、不同差分对和信号网的布线。电源/接地网布线在其指定的布线层上布线所有电源/接地线。差分对路由选择所有差分对，同时满足差分对约束。信号网络路由选择所有剩余网络。采用基于协商的路由器[22]来执行所有上述三种类型的路由，同时最小化违反设计规则的次数。在最后阶段，执行后处理以进一步减少设计规则违规的数量。

3.2 布线网格初始化

PCB设计可能包含各种预定义的障碍区域，称为路由禁止区域，指定的网络不应在其中路由。这些布线禁止由PCB设计者出于各种目的定义，并且可以是任意形状。为了遵守这些布线限制，我们将这些任意形状与SMD和通孔焊盘光栅化为三维布线网格，作为障碍，以便于后期导出无设计规则冲突的布线解决方案。图 5(a) 显示了由布线网格中的障碍物表示的布线禁区和焊盘的示例。 布线禁区和焊盘被障碍物完全封闭和覆盖，以避免违反设计规则。

图5：（a）在路由网格中，路由禁止和焊盘作为堆栈的示例。（b） 布线网络障碍物成本函数的横截面图。

3.3 迭代印刷电路板布线

在本节中，我们详细介绍了迭代PCB布线方案。为了执行逃逸路由和区域路由的任务，我们提出的统一路由方案是基于网格的 $ A^\ast $ 搜索算法[23]。通过调整 $ A^\ast $ 搜索算法的成本函数，我们能够使 $ A^\ast $ 搜索适应不同路由目标的需要。与以前的方案不同，这些方案分别路由每种类型的网络，然后将它们与专用方法结合在一起，以解决资源冲突。在我们的路由方案中，因为所有不同类型的网络都在同一个路由网格中路由，所以所有网络（包括电源/接地网络、差分对和信号网络）都可以一起协商路由资源，而无需任何手动调整或过于复杂的方法。

$ A^\ast $ 搜索成本函数 $ f(x) $ 表示路径 $ x $ 的成本,可以定义为：

$$f(x) = g(x) + h(x)$$

其中 $ g(x) $ 是从源到当前位置的成本 $ 𝑥 $ , 和 $ ℎ(𝑥) $ 是当前位置 $ x $ 到目标 $ t $ 的估计成本。由于我们的路由器支持135度和90度的路由角，在这项工作中，我们设计了估计函数 $ ℎ(𝑥) $ 成为：

$$\begin{align} minD = min(|x.x - t.x|, |x.y-t.y|),\\\\ maxD = max(|x.x-t.x|, |x.y-t.y|),\\\\ h(x) = maxD - minD + \sqrt{2} \times minD, \end{align}$$

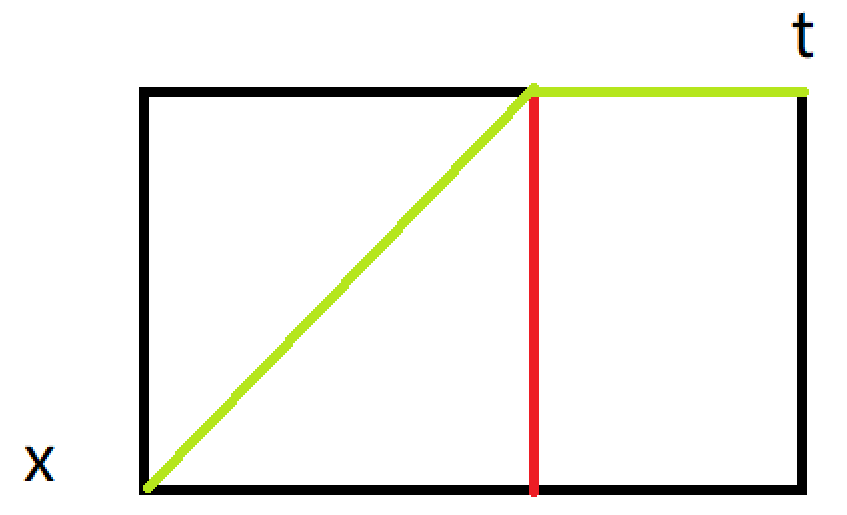
从这个135度角过去

其中 $ 𝑚𝑖𝑛𝐷 $ 是坐标差最小值， $ maxD $ 是坐标差最大值 。估计函数 $ ℎ(𝑥) $ 这里是可以接受的，它不会过分估计当前位置 $ x $ 到目标 $ 𝑡 $ 的实际成本，因此 $ A^\ast $ 搜索给出最优解。

此外，我们在每个路由迭代中为路由网络提出了一个新的障碍物成本函数。由于我们的迭代路由方案一个接一个地路由每个网络，因此先前路由的网络将成为以后路由的障碍。根据布线网络的宽度，它可能会占用多个网格单元作为障碍物（即软障碍物）。因此，从横截面角度来看，该成本函数被设置为根据每个网格单元到路由网络中心的距离来确定每个网格单元的值（即障碍物成本）。为了鼓励路由资源的协商，我们为路由网络设计了一个新的障碍物成本函数，如下所示：

$$\begin{align} OC_{routed\_net}(r) = H - H * \frac{|r|^c}{w^c}\\\\ c_i = c_{i - 1} * (\lambda + 1) \end{align}$$

其中 $ $ 𝑂𝐶_{𝑟𝑜𝑢𝑡𝑒𝑑\_𝑛𝑒𝑡} $ 是障碍物成本， $ 𝑟 $ 是到网中心的距离， $ 𝑤 $ 是网净宽度的一半， $ 𝐻 $ 是足够大以避免网络交叉的成本， $ 𝑐 $ 旨在调整网络边缘的成本（从横截面角度），以控制资源协商的水平，以及 $ \lambda $ 是用户定义的参数。例如，图5（b）给出了布线网络障碍物成本函数的横截面图。从绿色到蓝色再到红色虚线 $ 𝑐 $ 略微增加。换句话说，为了鼓励在早期阶段协商路由资源，可以选择由绿色虚线表示的成本函数。随着迭代的继续，可以利用红色虚线表示的成本函数来避免间距违规。

3.3.1 电源/接地网布线

为了使通用 $ A^\ast $ 搜索算法适应电源/接地网路由，我们必须调整成本函数 $ 𝑔(𝑥) $ 以实现在其指定的路由层上路由电源/接地网的需要。成本函数 $ 𝑔_{𝑝}(𝑥) $ 定义如下：

$$\begin{align} g_p(x) = \alpha * C_{layer} + \beta * C_{wl} + C_{obstacle}\\\\ C_{wl} = \gamma * C_{Euclidean} + C_{layer\_change} \end{align}$$

其中 $ \alpha,\beta,\gamma $ 是用户定义的参数， $ C_{layer} $ 是在特定层上路由的成本， $ C_{wl} $ 是累计走线长度的成本， $ C_{Euclidean} $ 是在同一层上走线的成本， $ C_{layer\_change} $ 是穿过不同层的成本（例如是使用电路板通孔的成本）， $ C_{obstacle} $ 是清除区域中障碍物的成本。使用此成本函数 $ 𝑔_𝑝(𝑥) $ , 我们可以在优选的路由层上找到当前路由电源/接地网的最小成本路径。

3.3.2差分对路由

我们的多层差分对路由方法包括四个步骤。

1. 第一步是为差分对的焊盘对的每一侧确定准确的候选合并点，从候选合并点开始差分对网络的路由将开始彼此平行。
2. 第二步是在来自焊盘对的每一侧的候选合并点之间以扩大的线宽度和间隙搜索区域进行布线。
3. 第三步是将第二步中的路由网分解为两个路由网，同时分解网的起点和终点仍然接近候选合并点。
4. 第四步是将每个分解网路由到其每一侧的相应焊盘上，并在BGA之间正确分配狗骨状通孔。请注意，在第二和第四步中，路由成本函数与信号网路由中使用的函数相同，将在后面详述。

图6：差分对路由示例。（a） 第一步是为差分对的焊盘对的每一侧确定候选合并点，其中差分对网络的路由将彼此平行。（b） 第二步是在来自焊盘对的每一侧的候选合并点之间布线，具有扩大的线宽度和间隙搜索区域。（c） 第三步是将路由网络从第二步解耦为两个路由网络。（d） 第四步是将每个去耦网络路由到每一侧的相应焊盘。

3.3.3 信号网络路由

为了使通用 $ A^\ast $ 搜索算法符合信号网络和差分对的路由，我们需要修改代价函数 $ 𝑔(𝑥) $ 以实现更好的路由解决方案。成本函数 $ 𝑔_𝑠(𝑥) $ 定义如下：

$$g_s(x) = \delta * C_{layer} + \epsilon * C_{wl} + \eta * C_{bend} + C_{obstacle}$$

其中 $ \delta,\epsilon,\eta $ 是用户定义参数， $ C_{layer} $ 是在特定层上路由的成本， $ C_{wl} $ 是累计走线长度的成本， $ C_{bend} $ 是累计弯曲次数的成本， $ C_{obstacle} $ 是清除区域中障碍物的成本。使用此成本函数 $ 𝑔_𝑠(𝑥) $ , 我们可以获得当前路由网络的最小成本路径，同时最小化弯曲和设计规则冲突的数量，并分配适当的狗骨通孔。

3.4 设计规则感知后处理

在最后一个阶段，我们执行各种后处理，以进一步减少违反设计规则的次数。在迭代PCB布线之后，所有网络都被布线而没有间距冲突，因此预留了用于后处理的空间。我们可以自由地稍微调整路由网络的段，而不必担心引入新的设计规则冲突。或者，我们可以插入其他填料。图7（a）和（b）显示了一种通过添加填充物来消除衬垫输入违规的方法。类似地，图7（c）显示了通过添加填充物或修改布线线段来修复T形交叉点违规的示例。

图7：（a）通过添加填充物以覆盖锐角来修复违反衬垫进入约束的锐角的示例。（b） 固定棉条的一个例子是，通过引入填充物来覆盖有限的间隔，从而违反了棉条进入规定。（c） 通过引入填充物或直接将T形结变为Y形结来解决T形结违规的示例

EXPERIMENTAL RESULTS

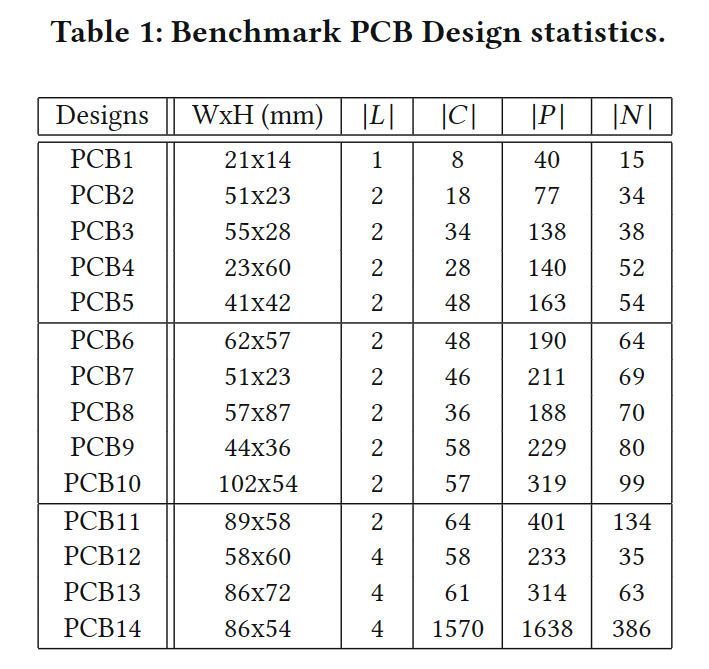
我们用C++编程语言实现了我们的算法。Boost C++库[24]用于计算我们提出的算法中的几何计算。所有实验都是在具有256GB内存的Intel Xeon 1.80GHz Linux机器上进行的，除了使用DeepPCB[25]的实验，这些实验是由DeepPCB的服务执行的。表1列出了实际学术和工业PCB设计的基准。“WxH”表示设计的宽度和高度尺寸。“|𝐿|”, “|𝐶|”, “|𝑃|”, 和“|𝑁 |” 分别表示PCB布线层、组件、焊盘和网络的数量。

如第1.2节所述，大多数先前的研究假设PCB设计采用常规BGA。然而，在实践中，一些SMD焊盘和通孔焊盘可能不在一个阵列的排列中，使得应用以前的工作来解决此类设计的路由任务具有挑战性。因此，为了证明我们提出的算法的效率和效果，我们将我们的算法与两个最先进的非学术性路由器DeepPCB和FreeRouting进行了比较。DeepPCB[25]是最近推出的基于人工智能的商业云端自动PCB布线服务。FreeRouting[26]是一个著名的用Java编写的开源PCB布线软件。此外，两个路由器都被设置为默认参数，并为我们的实验提供相同的输入设计和设计规则。对于我们的路由器，一个网格单元的宽度和高度是0.05毫米。KiCad[27]验证了不交叉、间隔和路由角度的约束，我们为其余的约束实现了一个设计规则检查器。

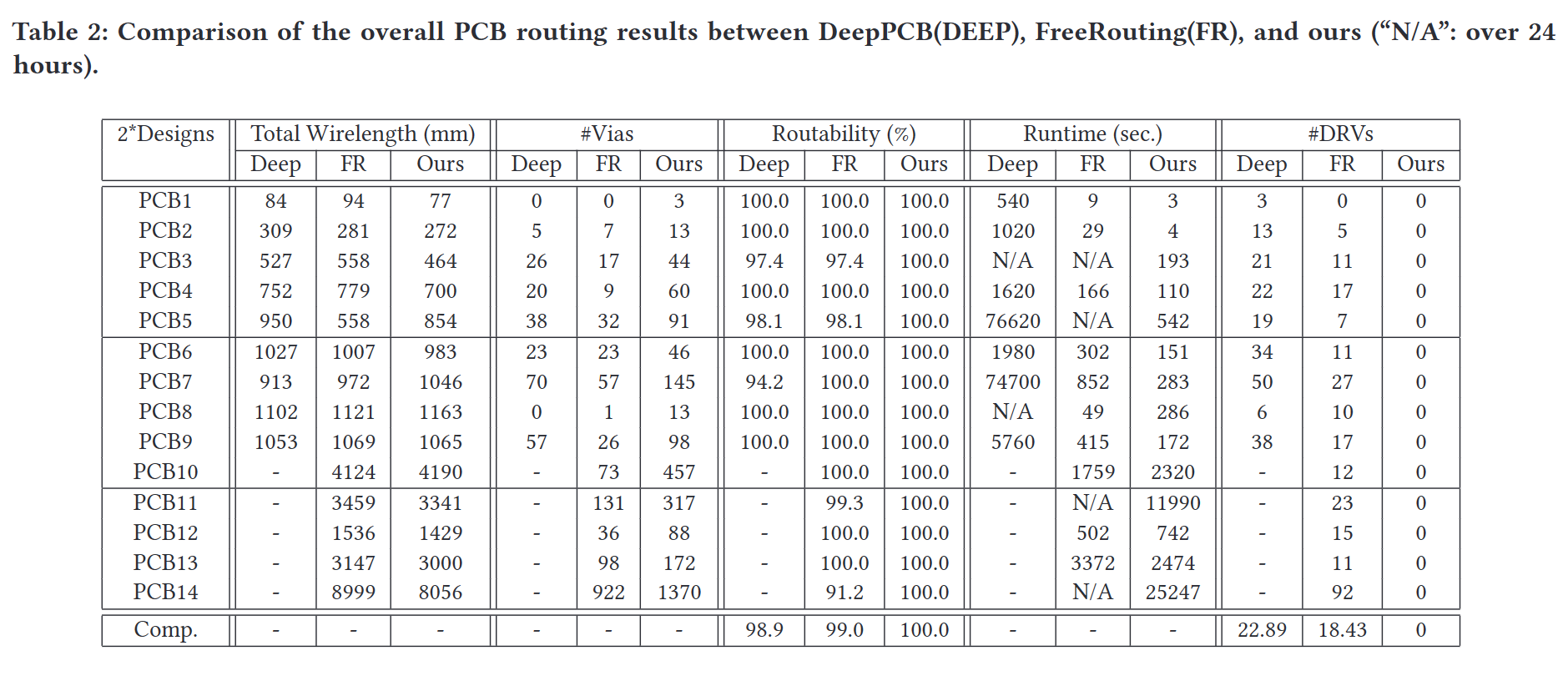
表2显示了实验结果，并报告了总导线长度、通孔数量、可布线性、运行时间和设计规则违规（DRV）总数。注意，此处DRV的数量包括第2.2节中提到的所有类型的违规行为。从结果可以看出，与DeepPCB（Deep）和FreeRouting（FR）相比，我们的算法可以在不违反任何设计规则的情况下实现所有14个基准的100%可路由性，而DeepPCB和FreeRoutings无法获得多个基准的路由解决方案，并导致不期望的设计规则违规。请注意，我们路由器的路由结果反映了更高的通孔使用率，因为我们的路由器被设置为将所有网络路由作为第一目标，然后将线路长度最小化。如结果所示，对于所有路由器完成路由（即100%可路由性）的测试情况，我们的路由器在所有路由器中给出了平均最短的总线路长度。此外，根据设计者的选择和设计的应用，我们提出的布线框架可以很容易地调整到最小化通孔数量或最小化总布线长度的偏好。因此，实验结果表明，对于SMD和通孔焊盘不规则排列的PCB设计的布线任务，我们的算法是灵活、有效和高效的。

图8:PCB14的PCB布线解决方案。黄色焊盘是通孔焊盘，红色网和SMD焊盘位于顶层，蓝色网位于第二层，粉色网位于第三层，绿色网和焊盘位于底层。

CONCLUSIONS

在本文中，我们针对SMD和通孔焊盘不规则排列的PCB设计，提出了一种统一的PCB布线算法。此外，我们在文献中首次提出了一种综合的多层PCB布线算法，该算法可以在统一的布线框架下一起处理电源/接地网络、差分对和信号网络。基于我们提出的多层差分对路由方案，我们有效地分配了狗骨通孔的位置，并在与所有其他网络协商路由资源的同时完成了差分对的路由。为了保持更好的可制造性，我们提出了一种有效的后处理方法，以进一步消除危害可制造性的不期望的设计规则冲突。实验结果证明了我们提出的算法的效率和有效性。