Luobuyu's Blog

0%

2014.岛

发表于 分类于 ， 热度： ℃ 评论：
本文字数： 1.8k 阅读时长 ≈ 2 分钟
感觉这个题目好像在哪见过，不太记得了，需要注意如果降低复杂度。

2014. 岛

题目描述：

每当下雨时，农夫约翰的田地总是被洪水淹没。

由于田地不是完全水平的，所以一些地方充满水后，留下了许多被水隔开的“岛”。

约翰的田地被描述为由 $ N $ 个连续高度值 $ H_1,…,H_N $ 指定的一维场景。

假设该场景被无限高的围墙包围着，请考虑暴雨期间发生的情况：

最低处首先被水覆盖，形成一些不连贯的岛，随着水位的不断上升，这些岛最终都会被覆盖。

一旦水位等于一块田地的高度，那块田地就被认为位于水下。

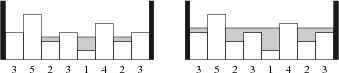
fig_islands.png

上图显示了一个示例：在左图中，我们只加入了刚好超过 $ 1 $ 单位的水，此时剩下 $ 4 $ 个岛（最大岛屿剩余数量），而在右图中，我们共加入了 $ 7 $ 单位的水，此时仅剩下 $ 2 $ 个岛。

请计算，暴风雨期间我们能在某个时间点看到的最大岛屿数量。

水会一直上升到所有田地都在水下。

输入格式

第一行包含整数 $ N $ 。

接下来 $ N $ 行，每行包含一个整数表示 $ H_i $ 。

输出格式

输出暴风雨期间我们能在某个时间点看到的最大岛屿数量。

数据范围

$ 1≤N≤10^5,1≤H_i≤10^9 $

输入样例：

1
2
3
4
5
6
7
8
9
8
3
5
2
3
1
4
2
3

输出样例：

1
4

题解：

这个题目还是很好的。

首先很容易想到是需要对高度排序，然后枚举高度，从最矮的一个开始淹没，这时岛的数量才会开始发生变化。对岛的数目取个最大值就行了。

但是难点是如何快速计算出岛的数量，肯定不能直接 $ O(n) $ 去遍历，这样会超时。能够想到的就是动态维护岛的数量。想要动态维护，那么就需要搞清楚岛的数量在什么时候开始发生了改变。

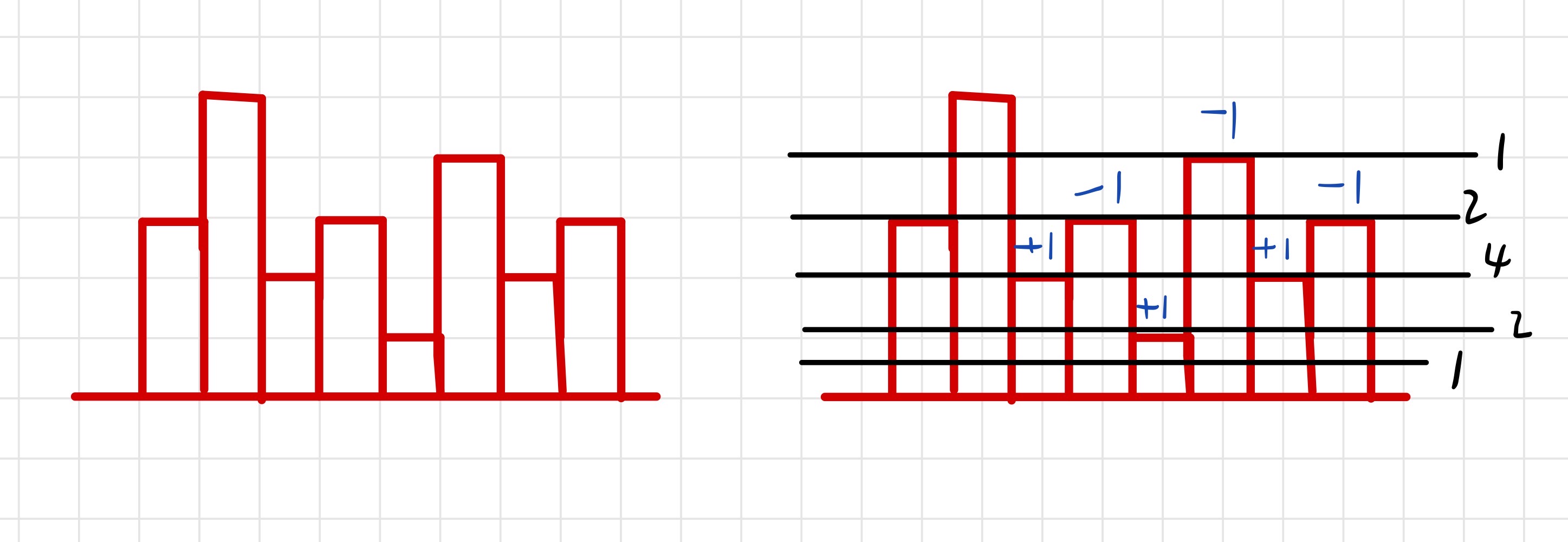
IMG_0104

很容易看到是在以下几种情况时发生了改变

IMG_0105

需要注意的是，淹没一个高度可能出现好几个 $ +1, -1 $ ，因此不能枚举到每一个时都更新，需要把该高度下的 cnt 变完之后才能更新 ans。

注意一下去重和离散化并不是一种操作。

离散化： {1e9, 1, 2, 1e5} 经过离散化后得到 {4, 1, 2, 3}，离散化并不改变数的大小关系，只改变数据本身的大小。离散化需要使用到 map.

去重：{2, 2, 3, 3, 2, 2, 4, 4} 经过去重得到 {2, 3, 2, 4}，去重是将连续的重复的给去掉，只保留一个。去重需要使用 unique.

这里可以看到例子 nowcoder多校(第八场) | Luobuyu’s Blog

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
using namespace std;
using namespace FAST_IO;
const ll mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF_LL = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-5;
const int maxn = 1e5 + 10;
const int maxm = 1e5 + 10;
int t, n, m, k;
int a[maxn];
pair<int, int> q[maxn];
int main()
{
// #define COMP_DATA
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    read(n);
    for (int i = 1; i <= n; i++)
    {
        read(a[i]);
    }
    // 去重
    n = unique(a + 1, a + 1 + n) - a - 1;
    // 离散化是需要把id进行映射，将 a[i] 比较大的数映射为比较小的
    // 可以使用 map 进行处理，分配 map.size() + 1
    for (int i = 1; i <= n; i++)
    {
        q[i] = {a[i], i};
    }
    sort(q + 1, q + 1 + n);
    int cnt = 1;
    int ans = 1;
    a[0] = a[n + 1] = 0;
    for (int i = 1; i <= n; i++)
    {
        int id = q[i].second;
        if (a[id] > a[id - 1] && a[id] > a[id + 1])
            cnt--;
        else if (a[id] < a[id - 1] && a[id] < a[id + 1])
            cnt++;
        // 其他两种是同构的，而且是cnt保持不变
        if (q[i].first != q[i + 1].first)
            ans = max(ans, cnt);
    }
    cout << ans << endl;
    return 0;
}