JSP问题描述

每个工序只有一台候选机器,因为每个工序机器都是固定的了,因此需要做的就是对每台机器上的工序进行排序,优化目标是使得完成时间最短,即 $ \min({\text{makespan}}) $ .

FJSP问题描述

就是每个工序有一组候选机器,在不同的候选机器上完成所需要的时间是不一样的(这样才有调度的必要),需要为每个工序确定机器,并且为机器上的工序排序。优化目标是使得完成时间最短,即 $ \min({\text{makespan}}) $
解的析取图表示
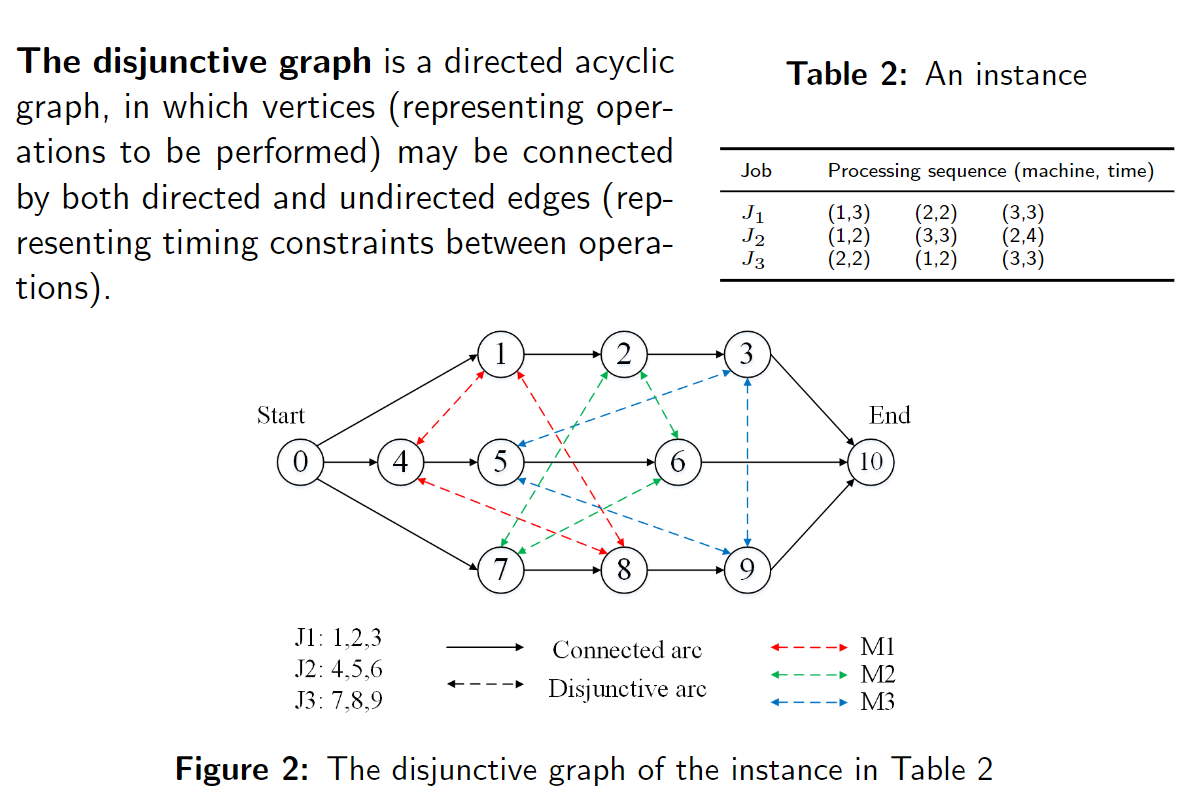
有向边是 job 的工序顺序限制,无向边是需要确定的,在 jsp 中,需要确定每台机器上的工序的顺序,实际就是确定这些无向边的方向。同时需要保证没有环。
关键路径和关键操作
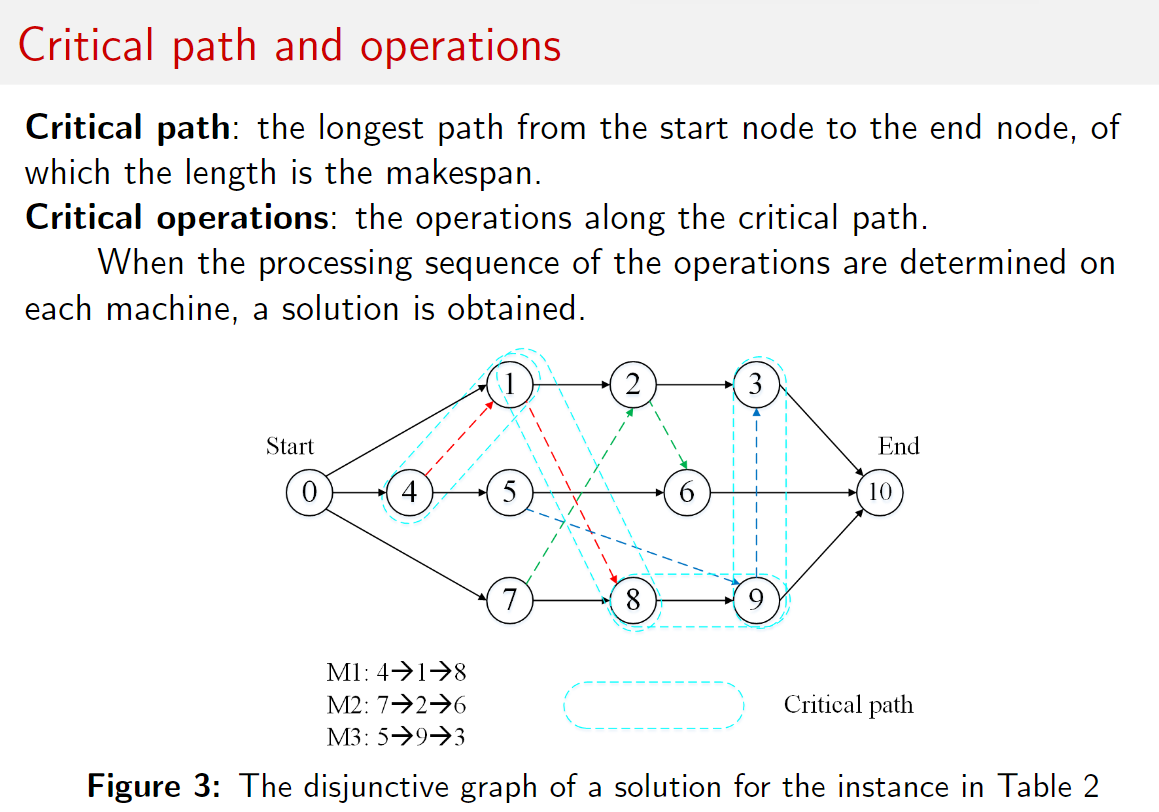
关键路径:从虚拟起始节点到虚拟终点的最长路
关键操作:就是关键路径上的操作。
job 序列中增加起点 start 和终点 end
关键块

关键块:就是在同一台机器上的连续的关键操作,就是一段关键序列。
在这个甘特图上,也可以找到关键路径,就是从最长的那个开始不断往前找紧贴着的块。
一些关键定理

- 在关键块内部改变操作的顺序,不能减少 makespan
- 在关键块外部改变操作的顺序,不能减少 makespan
- 所以,只有交换一个关键块内的操作和一个关键块外的操作才能减少 makespan
也就是移动操作的时候需要跨过另一种操作。
邻域结构
N5 邻域
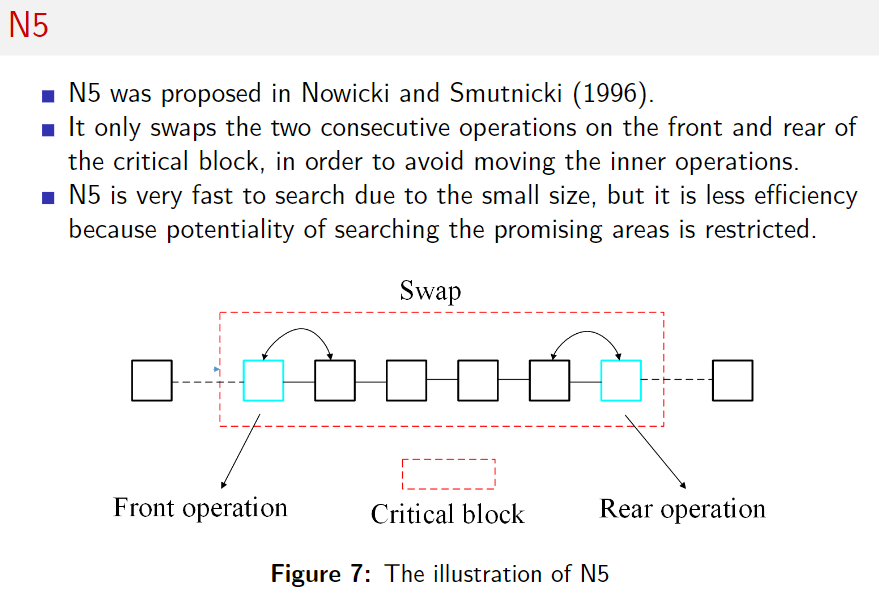
只交换关键块开头的两个,结尾的两个。奇怪,这不是在关键块内部操作的吗?为什么可以?
N6 邻域
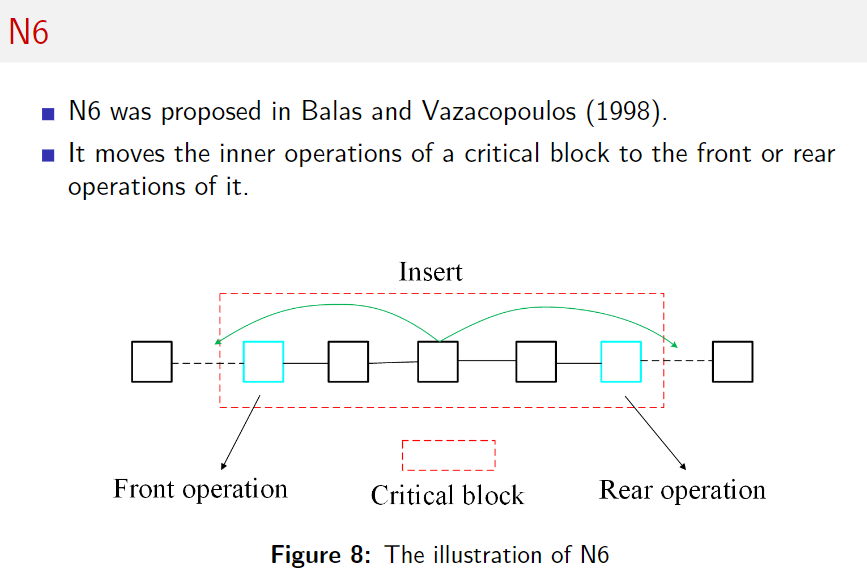
将关键块内部的操作移动到开头或结尾。
N7 邻域

将关键块内部的操作移动到开头或结尾,外加上把关键块开头或结尾的操作移动到内部。最有效的邻域动作
一些定义
predecessor:前驱
successor:后继
$ JP(i) $ :在同一工作中, $ i $ 的前驱节点
$ JS(i) $ :在同一工作中, $ i $ 的后继节点
$ MP(i) $ :在同一机器的工序中, $ i $ 的前驱节点
$ MS(i) $ :在同一机器的工序中, $ i $ 的后继节点
$ R(i) $ :从起始节点到 $ i $ 的最长路。(太怪了,命名完全没有道理啊,原来是这个意思)
$ Q(i) $ :从 $ i $ 到结束节点的最长路。
$ t_{o_{ij}k} $ :应该是两个下标, $ o_{ij} $ 和 $ k $ ,表示的是把 $ o_{ij} $ 放到 $ k $ 机器上的执行时间。
那么就可以得到
全是关于 $ i $ 节点和他的前驱后继之间的关系。他的 $ R(i) $ 和 $ Q(i) $ 是通过前驱后继搞出来的。
这样的话 makespan 就非常好算了
$ \text{makespan} = R(i) + t(i) + Q(i) $
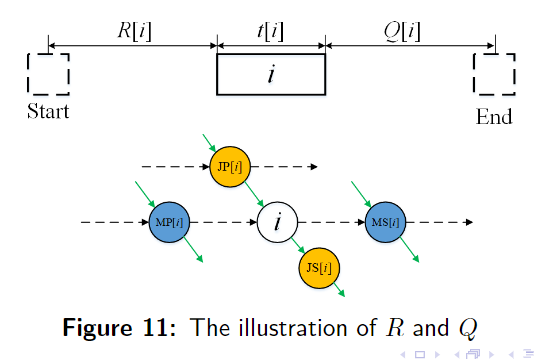
注意 $ JP,MP,JS,MS $ 是四个不同的点。
插入距离的估计
因为不能用真实计算,那样的话太费时了,所以使用的是估计。
makespan
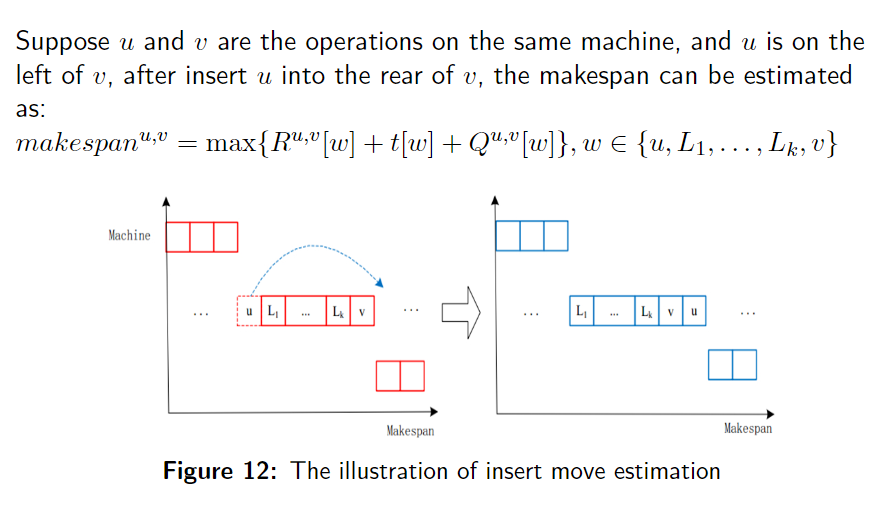
就是把 $ u $ 插入到 $ v $ 的后面之后,评估需要把 $ u,v $ 之间的都算一下,这样的话就是插入跨越的距离越短评估越快。
向后插入
估计 R
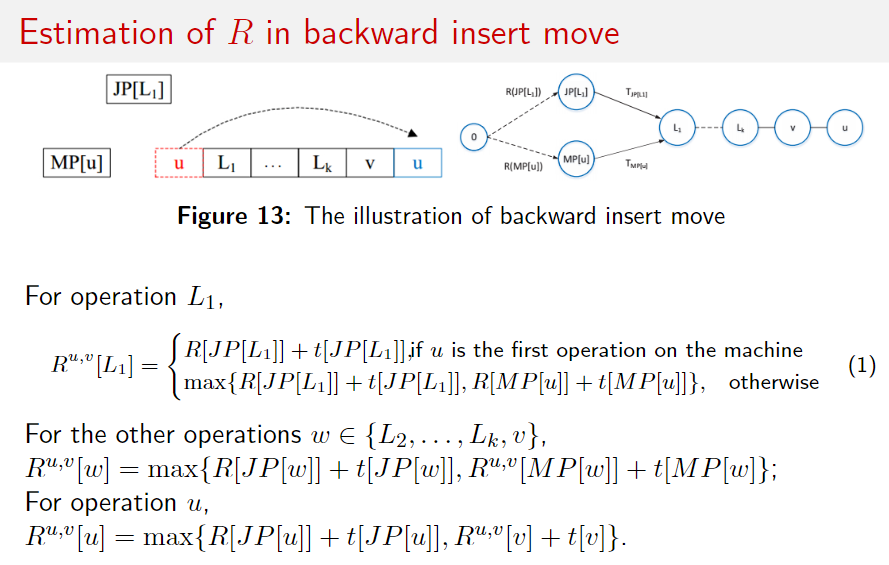
可以统一起来的,当 $ u $ 是机器上的第一个操作时,可以认为 $ MP(u) = start $ 。看来只能按照顺序算,先算出来前面的 $ R^{u,v} $ ,然后再递推出后面的,然后再算 $ Q $ 。
估计 Q
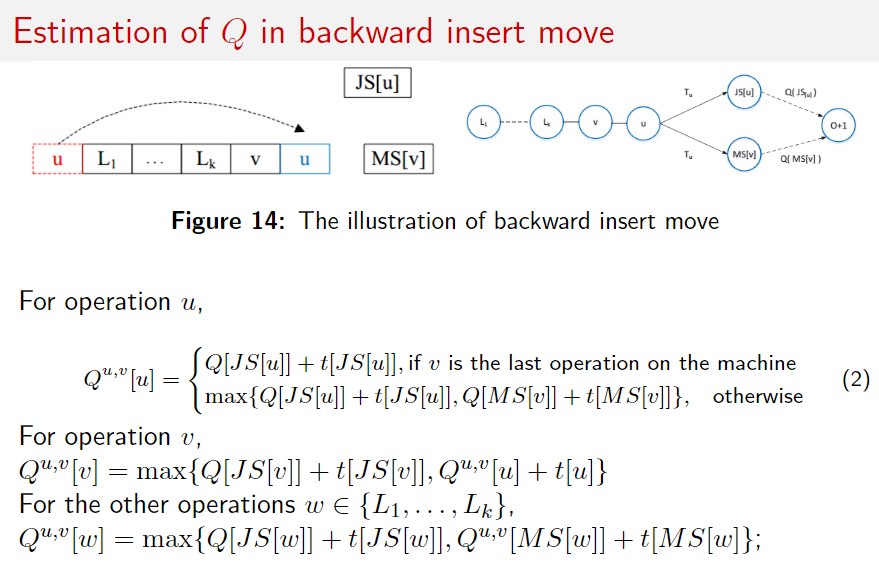
也可以统一起来,当 $ v $ 是机器上的最后一个操作时,可以认为 $ MS(v) = end $ 。看来需要从后往前算,先算出来后面的 $ Q^{u,v} $ ,然后再递推出前面的,然后再算 makespan。
向前插入
估计 R
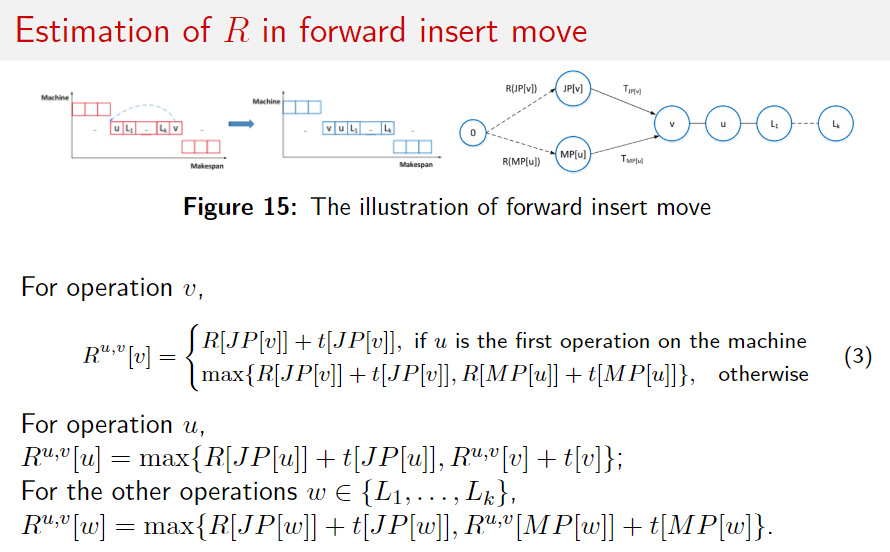
需要从前往后算了。

从后往前算。
更改机器分配时,估计 makespan

这个看着挺简单的。不知道效果如何
邻域结构
- 调整同一机器上操作的顺序,使用 $ N7 $ 邻域,(评估有点麻烦)
- 更改关键操作的机器分配,(评估比较简单)
禁忌操作

有点怪诶,禁忌的是关键块,禁忌表的长度不知道是多少。
距离定义
同一机器上的操作的距离定义为,二者的位置之差。
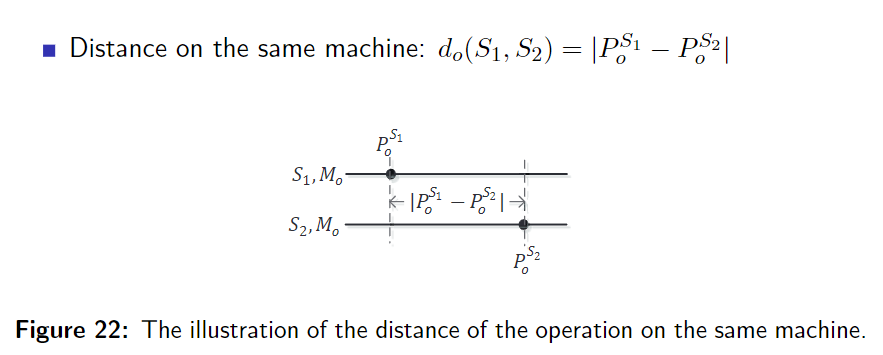
不同机器上的距离定义为移动到一起时,所需要的最短的距离。

从前面挪的话就是 $ P_o^{S_1} + P_o^{S_2} $ ,从后面挪的话就是 $ \left(L_{M_{o}^{S_{1}}}^{S_{1}}-P_{o}^{S_{1}}\right)+\left(L_{M_{o}^{S_{2}}}^{S_{2}}-P_{o}^{S_{2}}\right) $ ,其中 $ L_{M_{o}^{S_{1}}}^{S_{1}},L_{M_{o}^{S_{2}}}^{S_{2}} $ 表示 $ S_1,S_2 $ 所在机器序列的长度。
所以可以得到,两个解 $ S_1,S_2 $ 之间的距离为 $ d\left(S_{1}, S_{2}\right)=\sum_{i=1}^{n} \sum_{j=1}^{m} d_{o_{i j}}\left(S_{1}, S_{2}\right) $ ,需要找相同操作的距离。

对于 $ S_c $ 中的每一个操作,都要从他的 $ N^k $ 或 $ N^{\pi} $ 邻域中找到和 $ S_g $ 距离最小的解,然后加入 $ N $ 中。然后排除掉距离变大的。排序,随机从前几个中选一个。