针对有通信延迟的多处理器调度问题的可变邻域搜索 (VNS) 元启发式算法
摘要———本文的目的是提出一种可变邻域搜索
(VNS)元启发式算法,用于解决具有通信延迟 (MSPCD) 的多处理器调度问题。
MSPCD
问题考虑在多处理器系统上调度任务图,同时考虑到通信延迟。任务图包含优先关系以及任务之间交换的数据量。多处理器架构由一组以任意方式连接的相同处理器组成。通信定义为两个对称矩阵,分别包含每两个处理器之间的通信速率和访问成本。与文献中提出的
VNS
不同,我们使用不同的解决方案表示,从而定义两个自然邻域结构。计算经验显示了我们方法的优势。关键词:多处理器、任务调度、通信延迟、可变邻域搜索、VNS、元启发式。
一、介绍
在本文中,我们考虑具有以下特征的具有通信延迟的多处理器调度问题(MSPCD)。应该执行的任务之间的依赖关系被建模为有向无环图,其中顶点集对应于任务,弧集给出了任务之间的逻辑优先级,其中顶点和弧都被加权。顶点的权重表示任务处理时间,而弧的权重对应于任务间交换的数据量。假设计算网络(带有处理器的网络)由一个完整的图表示。我们在这里考虑同质情况,即计算单元是相同的。因此,通信网络中的顶点代表计算单元(处理器),边对应于每两个计算单元之间的通信介质。通信取决于任务之间交换的数据和计算单元之间的距离。目标是最大限度地缩短完工时间,即最后一个待处理任务的结束时间。
然后,问题是如何有效地将任务映射到处理网络上。我们必须将任务分配给处理单元,使每个任务都尊重优先级和通信约束,以确保保留原始程序的语义。因此,对于每项任务,我们需要确定其开始执行的时间和负责其执行的处理单元。必须处理每项任务,并根据可用资源规划整个图表。必须尊重执行任务之间的优先级和通信。请注意,只有当某个处理器可以使用来自其前一个处理器的所有数据时,才能在该处理器上执行任务。分配给同一处理单元的任务之间没有重叠。每个处理单元在同一时间只能执行一个任务。在我们的情况下,不允许抢占。
本文的主要贡献是一个实用的贡献﹐我们调整并应用可变邻域搜索(VNS)元启发法来解决有通信延迟的多处理器调度问题(MSPCD)。我们引人了一个新的GVNS,并对解决方案进行了新的表述。解决方察的编码允许定义丰富的邻域结构,从而能够更好地快速探索所有潜在的解决方案。
本文组织如下。第2节给出了问题的描述。在第3节中,我们介绍了我们的元启发式算法。然后我们在第4节总结这项工作。
二、相关的工作
Rayward-Smith [21] 是第一个在解决 MSP时解决通信延迟问题的人。他研究了具有单元通信延迟的情况,证明它是NP-hard,并提出了一个广义的列表调度算法。
Chr ́etienn 和 Picouleau [10]对通信延迟的一般情况进行了调查。他们列出了MSPCD上的现有变体,概述了它们的复杂性和解决方法。解决方法。对于每一类﹐他们描述了目前关于容易和困难问题之间的知识。由于 MSPCD 问题是NP-hard(参见例如[18]、[14]),因此大部分工作涉及基于元启发式的解决方案技术。此外,实际的调度问题更加困难,因为它们包含额外的侧面约束和/或优化多个目标。Hwang等人[15]对具有通信费用的相同处理器的情况进行了算法比较。Luo等人[17]回顾了20种无通信情况下的贪心算法。在[20]中,有通信延迟的m-machine问题已被证明对于任意的优先级关系是NP-complete的,即使是两个处理器。然而,有一些特殊的类别可以构建多项式时间算法([8],[16],[20])。尽管如此,在开发有效的启发式方法之前,研究人员通常从正在研究的调度问题的数学规划公式开始。尽管已经开发了几种数学规划模型,但由于模型制定和/或计算上的困难[23],它们通常在实际的问题实例中表现得不是很好[23]。Unlu和Mason [23]概述了在没有通信的情况下不同的数学规划公式。他们根据四种不同类型的决策,记录了四种不同的混合整数规划(MIP) 公式。分配和位置预定变量 [11]、线性排序变量 [19]、时间索引变量[22]和网络变量[9]。我们在审查中确实遇到了三种考虑到通信延迟的方法:Davidovic´等人 [12]、[13] 和 Venugopalan 和 Sinnen [24]。
在我们遇到的文献中,也有一些使用 VNS元启发式算法来解决这个问题的案例。Davidovi ́等人 [12] 提出了一种VNS,其解决方案如同 TPS 问题中的排列组合。对 VNS的贡献仍然有限,我们尝试在本文中为解决 MSPCD 问题的 VNS方法添加一些贡献。
三、MSPCD的可变邻域搜索(VNS)元启发式算法
可变邻域搜索 (VNS)是一种用于解决组合优化和全局问题的元启发式方法。它是由Mladenoví和Hansen于1997提出的[1]。它使用当前现有解决方案的不同邻域结构,如果没有改进,就从一个邻域迁移到另一个邻域。邻域的变化分两个阶段完成:(1)寻找局部最优的下降阶段和(2)走出局部最优区域的扰动阶段。VNS被应用于许多领域,如位置理论、聚类分析、调度、车辆路线、网络设计、批量大小、人工智能、工程、集合问题、生物学、系统发育、可靠性、几何学、电信设计等等。关于VNS的一般调查见[2]、[3]、[4]、[5]。
在这一节中,我们介绍了本文的主要贡献。我们为 MSPCD调度问题提出了一个通用 VNS (GVNS)解决方案。 GVNS 是 VNS的一个变种,其中在基本的 VNS 方案中使用可变邻域下降 (VND)局部搜索。在本文的其余部分中,我们将需要使用以下符号:
N: n 个任务的集合;
M: m 个处理单元的集合;
$ G = (N,A) $ : 给定的有向无环图 (DAG),A
是表示任务之间优先级的边的集合,即 A 中的 $ (i,\ j) $ 表示任务 i
必须在任务 j 之前执行。 $ \ |A| $ 是G中的边数;$ Pred(i) $ :任务 i之前的任务集,即
$ Pred(i) = \{ j \in N:(i,j) \in A\} $ ;$ Succ(i) $ :接替 i的任务集,即 $ Succ(i) = \{ j \in N:(j,i) \in A\}; $
$ S\lbrack k\rbrack $ :分配给计算单元的任务序列k;
$ t_{i} $ :任务 i 的处理时间;
$ C_{ik,jl} $ :处理单元 k 上的任务 i 和处理单元 l 上的任务 j
之间直接通信的成本(通信延迟);$ \text{Cmax} $ :makespan,执行所有任务的总时间。
A. Neighborhood
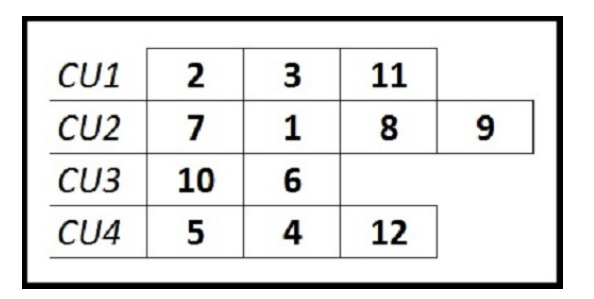
MSPCD 的解决方案是由 m 个序列的列表 S 表示。对于每个计算单元 k,S[k]是一组分配给 k的任务以及它们的执行顺序。图1显示了一个解决方案编码的例子。在这个例子中,任务2,3 和 11被分配到计算单元CU1,它们是按照给定的顺序执行。通过这种解决方案的表示,我们可以使用几种邻域结构,但有两个明显的结构是:(1)在同一处理单元内重新排序任务或(2)将一个任务从一个处理单元移动到另一个处理单元。这些结构最适合我们的调度问题。因为要么一个资源负载过大,所以我们将任务转移到一个资源,或者计划有太多延迟,所以我们重新排序任务。我们也可以两者都做。
我们使用的两个邻域结构是:
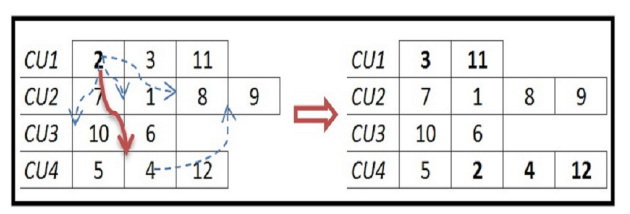
InterInsertion N1.可行解 x 的 InterInsertion
邻域是通过将一个任务从一个计算单元中的一个位置移动到不同计算单元中的另一个位置来定义的。图
2 显示了一些可能的移动,并给出了图 1 解决方案的一个 InterInsertion
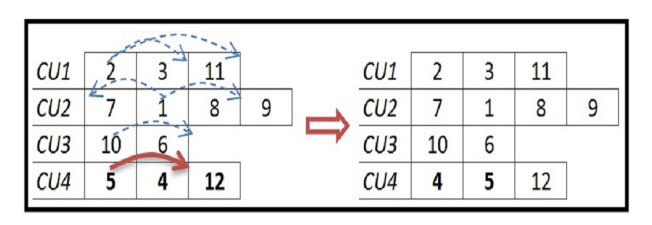
邻域。可能的 InterInsertion 总数介于 n(m - 1) 和 n(m-1)(n + m)/m 之间。IntraInsertion N2.可行解 x 的 IntraInsertion
邻域是通过在相同的计算单元中将一个任务从一个位置移动到另一个位置来定义的。图
3 显示了一些可能的移动,并给出了图 1 解决方案的一个 IntraInsertion
邻域。插入可以是向后或向前的。可能的 IntraInsertion 总数介于
$ \left( (n - m)^{2} \right)\text{/}m\ $ 和 $ n^{2} + m - 2n $ 之间。
在这两种结构中,一个解决方案的邻域总数约为 $ n^{2} $ 。并非所有插入都会产生可行的解决方案。事实上,可行的移动的数量取决于任务图的密度。在我们的元启发式方法中,我们包含了一个检查解决方案可行性的程序。此过程这个程序检查在新位置上是否有一个任务既未安排在它的前一个任务之前,也没有安排在它的后一个任务之后,即检查可行性。
B. Initial solution and Cmax lower bound
为了计算初始解决方案,我们使用Ait El Cadi 等人[1]的贪构造启发式(GCH)。同样的,对于 $ C_{\max} $ 的下限,我们使用Ait El Cadi等人[1]的工作中提出的前向传递算法。
C. The fitness function
为了评估给定的解决方案,我们开发了一种启发式算法,可以从一个序列列表中计算出一个时间表。该算法工作如下:
(1) 我们将集合 I 初始化为没有前置任务的集合,计算单元 j 可用的时间a(j) 初始化为零。
(2) 我们从集合中选择任务 I 和序列列表、解决方案 S、任务 i和尚未调度的相应处理器 H(i)。
(3) 我们更新所选处理器的 a(H(i)),并添加 i 的所有直接继任者到 I,并且从 I 中删除 i。
(4) 我们重复步骤 2 和 3 直到集合 I为空。在此算法中,我们将要处理的最后一个任务的结束时间保存在内存 U 中。最后, $ C_{\max} $ 由 U 给出。
D. Variable Neighborhood Descent (VND) for the MSPCD
它是 VNS 的确定性变体。我们使用 VND 作为 GVNS的局部搜索程序,以获得与所有预定义的邻域结构有关的局部最小值。在我们的VND 程序中,我们使用两个邻域结构 N1 和N2。每次移动要么是对任务的重新排序,要么是在计算单元之间移动任务。我们决定通过首先在处理器和处理器之间移动任务来探索邻域结构,只要有改善就继续。一旦没有可能改进,我们就移动到第二个邻域结构N2。我们通过前后移动每个处理器中的任务将他们进行重新排序,直到不可能改进,然后我们停止,否则我们返回到邻域结构N1。这些邻域结构中的每一个都是通过使用最佳改进搜索策略来探索的。然而,在下一个邻域结构中继续搜索当前解决方案的改进,而不管在先前的邻域结构中是否找到了改进。
VND的步骤是:
重复以下顺序,直到没有得到改善。

E. Shaking procedure
扰动程序是用来避免局部最小值的。它的作用是以渐进的方式使搜索远离当前的局部最小值。参数k,即移动次数,校准我们将从局部最小值逃脱的距离。在 VNS
启发式过程中,k 的值会增加,直到达到最大值 $ k_{\max} $ 。在我们的例子中,扰动是在两个邻域结构中随机进行的,如下所示:
(1) 随机选择一个邻域结构
(2) 在所选结构中随机选择第 k 个邻域。
我们的摇动程序可能导致不可行的解决方案。在这种情况下,扰动的结果将被丢弃,我们再次重新扰动。
F. GVNS
我们的 GVNS 的实现如下:

上述 GVNS 包含 2 个参数: $ t_{\max} $ ,搜索中允许的最大时间; $ k_{\max} $ ,与现有解决方案的最大距离。当总运行时间大于 $ t_{\max} $ 时,GVNS 终止。在内部循环中,现有解决方案x 移动,直到在与其最大距离 $ k_{\max} $ 的邻域中没有检测到改进。
四、实验结果
A. Benchmark instances
Davidovic´等人在[7]中描述了基准实例。在那篇论文中,他们为同构处理器提出了测试问题实例,但存在通信延迟。它们的实例在处理器数量、多处理器架构类型、要调度的任务数量和任务图特征(任务执行时间、通信成本和任务之间的依赖关系密度)方面具有代表性。此外,他们的任务图生成器以适当的方式定义,以确保相应的问题实例遵守最近在文献中提出的理论原则。他们提出了两组任务图,用于分析和比较解决有通信延迟的(同质)多处理器问题的启发式方法。第一个是由随机生成的DAG 组成。在这个集合中,每个文件都有一个以 t开头的名称,并以以下数字为后缀:任务数,边缘密度 $ D = 2|A|\text{/}\left( n(n\ - \ \ 1) \right) $ ,和用于区分具有相同特征的图形的索引。第二组包含具有给定多处理器架构的已知最佳解决方案的任务图。此类文件的名称以ogra开头,后缀为:该文件中的任务数和边密度。根据[13],第二组问题具有一个特殊的结构,当相互独立的任务数量很大时,很难找到产生最优解的任务排序。
整个测试在一台具有 8GB RAM和 8 核 Intel 处理器 i7-3740QM的笔记本电脑上进行。操作系统是 64 位 Windows 7专业版。所有算法和启发式都是使用 OPL 脚本语言实现的。
B. Results
表 I 展示了我们的方法在平均规模问题上的结果。测试是在 $ t_{\max} = 120\text{sec} $ 和 $ k_{\max} = 10 $ 时进行的。第一列给出了计算单元的数量,第二列给出了任务的数量,第3列和第 4列给出了 VND 和 GVNS的CPU时间,最后两列给出解决方案的改进百分比。似乎在很短的时间内,即几秒钟内,目标就能提高3% 到 10%。
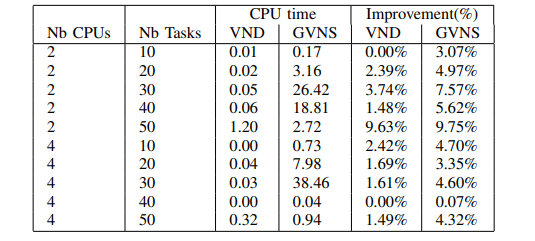
表 2 展示了我们的 GVNS 在大型实例上的性能。 Davidovic´等人[7]提供的一些实例有一个已知的最优解。表 2的各列分别显示了实例名称、已知最佳值、我们的下限、VND 和 GVNS CPU时间以及 VND 和 GVNS 找到的目标值。结果很好,但仍需要一些改进。我们的GVNS需要对其参数、扰动和局部搜索程序就行改进。
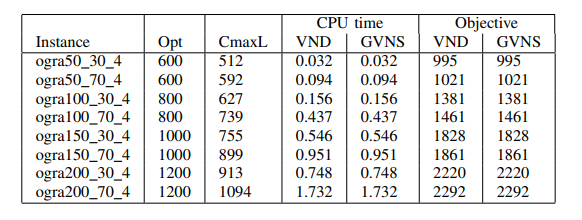
表 2.VND和 VNS 在大实例上的结果 已知最优( $ t_{\max} = 60\text{sec} $ 和 $ k_{\max} = 10 $ )。
表 3 将我们的结果与 Ait El Cadi 等人在 CPLEX下求解数学模型的结果进行了比较[6]。这些实例具有全部 50个任务,但计算单元数量不同,分别为 2、4 和 8个,以及用于网络的超立方体架构。在 [6] 中,CPLEX 时间限制设置为 120秒。从表中可以看出,我们的 GVNS 即使在几秒钟内也有很好的结果,不到 6秒,它更接近于 CPLEX 的解决方案。
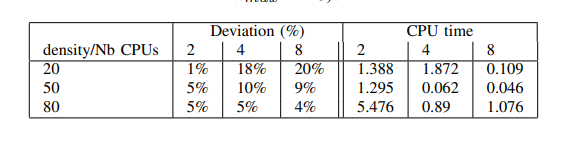
表 3.CPLEX 之间的比较结果(来自[6])和 VNS 用于具有 50 个任务的案例( $ t_{\max} = 60 $ 秒和 $ k_{\max} = 10 $ )。
五、结论
我们将可变邻域搜索应用于众所周知的具有通信延迟的多处理器调度问题。我们提出了一种通用变量邻域搜索(GVNS) 元启发式算法来解决MSPCD。结果表明,我们的方法很有希望,在几秒钟内,我们就能得到很好的结果。然而,我们的元启发式仍然需要一些改进。未来的工作是通过考虑两个邻域结构之间的循环过程来改进VND 局部搜索过程。 GVNS参数,尤其是k,需要一些微调。邻域太大,需要减少,或者探索应该更有效。
参考文献:
[1] Mladenovi ́c, N., Hansen, P., Variable neighborhood search,Computersand Operations Research 24 (11): 10971100 (1997).
[2] Hansen, P., Mladenovi ́c, N., Perez, J.A.M., Variable neighbourhoodsearch: methods and applications, Annals of Operations Research 175:367407 (2010).
[3] Hansen, P., Mladenovi ́c, N., and Moreno-P`erez, J.A., Variable neighbourhood search: methods and applications (invited survey), 4OR, 6:319-360(2008).
[4] Hansen, P., Mladenovi ́c, N., An introduction to Variable Neighborhood Search. in S. Voss, editor, metaheuristics, Advances and Trends in Local Search Paradigms for Optimization, 433458, Kluwer Academic Publishers, Dordrecht, (1999).
[5] Hansen, P., Mladenovi ́c, N., Variable Neighborhood Search: Principles and Applications. European J. Oper. Res. 130 (3): 449-467, (2001).
[6] Ait El Cadi A., Ben Atitallah R., Hanafi S., Mladenovic N., Artiba A., New MIP model for Multiprocessor Scheduling Problem with Communication Delays, Optimization Letters (DOI: 10.1007/s11590-014-0802-2) (2014).
[7] Davidovi ́c, T., Crainic, T.G.: Benchmark-problem instances for static scheduling of task graphs with communication delays on homogeneous multiprocessor systems. Comput. Oper. Res. 33, 21552177 (2006)
[8] Ali H., H., El-Rewini, H.: An optimal algorithm for scheduling interval ordered tasks with communication on N processor, University of
Nebraska at Omaha, Math. And Computer Science Department, Technical Report, 9120 (1990)
[9] Cakici, E., Mason, S. J.: Parallel machine scheduling subject to auxiliary resource constraints. Production Planning and Control, 18, 217225 (2007)
[10] Chr ́etienne, P., Picouleau, C.: Scheduling with communication delays: A survey. In: Chr ́etienne, P., Coffman, E.G., Lenstra, J.K., Liu, Z.
(eds.) Scheduling theory and its applications, pp. 6590. John Wiley & Sons, New York (1995)
[11] Dauz`ere-P ́er`es, S., Sevaux, M.: Using Lagrangean relaxation to min- imize the weighted number of late jobs on a single machine. Naval Research Logistics, 50(3), 273288 (2003)
[12] Davidovi ́c, T., Hansen, P., Mladenovi ́c, N.: Permutation-based Genetic, Tabu and Variable Neigh-borhood Search Heuristics for Multiprocessor Scheduling with Communication Delays. Asia-Pacific Journal of Operational Research, 22(3), 297326 (2005)
[13] Davidovi ́c, T., Liberti, L., Maculan, N., Mladenovi ́c, N.: Towards the optimal solution of the multiprocessor scheduling problem with communication delays. MISTA Proceedings (2007)
[14] Garey, M.R., Johnson, D.S.: Computers And Intractability: A Guide To The Theory Of NP-Completeness. WH Freeman & Co., San Francisco (1979)
[15] Hwang, R., Gen, M., Katayama, H.: A comparison of multiprocessor task scheduling algorithms with communication costs. Computers & Operations Research, 35, 976993 (2008)
[16] Isaak G.: Scheduling rooted forests with communication delays. Order 11, 309316 (1994)
[17] Luo, P., L, K., Shi, Z.: A revisit of fast greedy heuristics for mapping a class of independent tasks onto heterogeneous computing systems. Journal of Parallel and Distributed Computing, 67, 695714 (2007)
[18] Murty, K.G.: Operations research: deterministic optimization models. Prentice-Hall, Englewood Cliffs, NJ (1994)
[19] Pinedo, M.: Scheduling: Theory, algorithms, and systems (2nd ed.). Prentice-Hall, New Jersey (2002)
[20] Prastein, M.: Precedence-constrained scheduling with minimum time and communication. MS Thesis, University of Illinois at Urbana- Champaign (1987)
[21] Rayward-Smith, V.J.: UET scheduling with unit interprocessor communication delays. Discrete Applied Mathematics, 18, 5571 (1987)
[22] Sousa, J. P., Wolsey, L. A.: A time-indexed formulation of nonpreemptive single machine scheduling problems. Mathematical programming, 54,353367 (1992)
[23] Unlu, Y., Mason, S. J.: Evaluation of mixed integer programming formulations for non-preemptive parallel machine scheduling problems. Comput. Ind. Eng., Pergamon Press, Inc., 58, 785800 (2010)
[24] Venugopalan, S., Sinnen, O.: Optimal Linear Programming Solutions for Multiprocessor Scheduling with Communication Delays. In: Xiang, Y.,Stojmenovic, I., Apduhan, B.O., Wang, G., Nakano, K., Zomaya, A. (Eds.) Algorithms and Architectures for Parallel Processing,
Springer, Heidelberg, 7439, pp. 129138 (2012)