A Two-Individual Based Evolutionary Algorithm for the Flexible Job Shop
摘要
基于种群的进化算法通常要管理大量的个体以保持搜索的多样性,这是很复杂和耗时的。在本文中,我们提出了一种只使用两个个体的进化算法,称为师徒进化算法(MAE),用于解决灵活的工作车间调度问题(FJSP)。为了保证进化的多样性和质量,MAE考虑到FJSP的多种复杂约束,整合了一个Tabu搜索程序,一个基于路径重联的重组算子,以及一个有效的个体更新策略。在313个广泛使用的公共实例上的实验表明,MAE在47个实例上改进了以前的最佳结果,在除3个以外的所有剩余实例上与已知的最佳结果相匹配,而消耗的计算时间与目前最先进的元启发式方法相同。MAE还为10个困难实例建立了解决方案的质量记录,这些实例以前的最佳值是由一个著名的工业求解器和一个最先进的精确方法建立的。
一、介绍
工作车间调度问题(JSP)是一个强 NP-hard 问题(Garey, Johnson, and Sethi 1976)。在这个问题中,有一组工作 $ J=\{J_1, \cdots , Jn\} $ ,必须在一组 $ M = {M_1,\cdots, M_m} $ 的机器上处理。每个作业 $ J_i, i = 1, \cdots , n $ ,由 $ n_i $ 个操作 $ O_i = {o_{i1}, \cdots , O_{ini} } $ ,应按顺序处理。此外,每个操作 $ O_{ij} $ 都需要在整个处理时间内不间断地独家使用其分配的机器。灵活的工作车间调度问题(FJSP)是JSP的扩展,它允许一个操作 $ O_{ij} $ 在一组候选机器 $ M(O_{ij}) \subseteq M $ 上处理。操作 $ O_{ij} $ 在机器 $ M_k \in M(O_{ij}) $ 上的处理时间用 $ t_{O_{ij}k} $ 表示。问题是将每个操作分配给一台机器,并对机器上的操作进行排序,使得所有工作的最大完成时间(即makespan)达到最小。
自从FJSP由(Brucker and Schlie 1991)提出以来,文献中提出了大量的方法来解决它。在这些方法中,我们引用了几种精确的方法。Thomalla 2005)提出的基于拉格朗日松弛法的离散时间整数编程,Özgüven, Özbakr和Yavuz 2010)提出的具有路由和流程计划灵活性的混合整数线性编程模型,以及Hansmann, Rieger和Zimmermann 2014)提出的与分支和边界算法相结合的混合整数线性优化模型。其他基于混合整数线性规划的精确方法可以在(Gomes, Barbosa-Pvoa, and Novais 2013; Roshanaei, Azab, and Elmaraghy 2013)找到。
对于大型FJSP实例,已经采用了各种元启发式算法。值得注意的文献包括。(Brandimarte 1993), (Dauzère-Pérès and Paulli 1997), (Mastrolilli and Gambardella 2000), (Pezzella, Morganti, and Ciaschetti 2008), (Gao, Sun, and Gen 2008), (Oddi et al. 2011),(Bo˙zejko, Uchro´nski, and Wodecki 2010),(Gutiérrez and Garc´ıa-Magari˜no 2011),(Li, Pan, and Liang 2010),(Wang et al. 2012),(Wang et al. 2013),(Yuan and Xu 2013a),(González, Vela, and Varela 2013)和(Gao et al. 2016)。最近的方法包括攀登深度边界差异搜索(CDDS)算法(Hmida, Haouari, and Lopez 2010)、混合差分进化算法(HDE-N2)(Yuan and Xu 2013b)、带路径重联的散点搜索(SSPR)(González, Vela, and Varela 2015)、遗传标签搜索(HGTS)(Palacios et al. 2015年),带有Tabu搜索的混合遗传算法(HA)(Li和Gao 2016年),以及多起点多层次进化局部搜索(GRASP-mELS)(Kemmoé-Tchomté, Lamy, and Tchernev 2017年)。尽管这些方法在所有基准的解决方案质量和计算效率方面都不占优势,但CDDS、HDE-N2、SSPR、HGTS、HA和GRASP-mELS在这些方法中表现得最好。
基于种群的进化算法在解决FJSP问题上有很好的性能。然而,他们面临着管理大量个体以保持搜索多样性的缺点(Lahiri和Cebrian,2010)。在本文中,我们提出了一种仅使用两个个体的进化算法,称为师徒进化(MAE)算法,用于求解FJSP,灵感来自HEAD(Moalic and Gondran 2017),这是我们所知的唯一一种基于两个个体的进化算法。HEAD用于解决k-着色问题。k-着色问题的特殊性在于其约束非常简单,而FJSP具有多个复杂约束。因此,HEAD和MAE必须非常不同:HEAD使用贪婪分割交叉生成子解,因为它在不可行解空间中搜索可行的k-着色,而MAE使用基于路径重新链接的重组算子和新的距离定义生成子解,因为它在可行解空间中寻找最优可行解。事实上,交叉算子通常会为FJSP生成不可行的子解,修复这些解会导致较差的解,而基于路径重新链接的重组算子可以更容易地控制以生成可行的子解。此外,交叉算子还保持了头部搜索的多样性,而MAE则通过在两个个体接近时直接用随机可行解替换一个个体来保持多样性。在(Duarte et al.2005)中可以找到两个单独的记忆算法与常规重新初始化相混合的类似尝试。
本文的剩余部分组织如下:第2节介绍了所提出的MAE算法。第3节将MAE与最先进的算法进行了比较,并分析了MAE的关键特征,以确定其成功因素。第四部分总结全文。
二、Master-Apprentice Evolutionary Algorithm
师徒进化算法的思想起源于社会活动,学徒从他们的主人那里获得知识。当两个学徒(个体)在给定的世代(一个周期)内进化时,他们会成为大师,并且有很多相似之处。因此,当一个周期结束时,一个学徒被上一个周期中的大师替换,以继续进化,从而吸收历史(上一个周期)的精髓。这就是为什么我们称这种算法为师徒进化算法。
基于两个个体的进化机制是MAE的一个独特特征。传统的基于种群的进化算法通常面临着种群数量大、计算资源消耗高的缺点。通过使用有效的个体更新策略管理两个个体,MAE可以在多样化和搜索效率之间实现更好的权衡。在本节中,我们首先介绍MAE的总体架构,然后介绍其不同组件。
2.1 Main scheme of MAE
MAE遵循进化算法的基本框架(吕、格洛弗和郝2010;萨顿和诺依曼2012;于、姚和周2013)。其示意图如图1所示,其总体架构如算法1所述。该算法有三个主要组成部分:用于生成随机解的 Init() 函数、用于改进解 S 的禁忌搜索过程 TS(S) 以及用于生成两个子解的基于路径重新链接的重组算子。这些世代被划分为长度为 p 的循环,其中 p 是一个整数参数。当前(上一个)循环中的最优解存储在 $ S_c^ (S_p^) $ 。开始时,MAE生成两个随机解 $ S_1 $ 和 $ S_2 $ 。然后,在每一代中,它在 $ S_1 $ 和 $ S_2 $ 上应用基于路径重新链接的重组算子来生成两个子解 $ S_{1}^{\prime} $ 和 $ S_{2}^{\prime} $ ,然后通过禁忌搜索过程对其进行优化,以成为新的 $ S_1 $ 和 $ S_2 $ 。如果新的 $ S_1 $ 或 $ S_2 $ 优于 $ S_c^ $ ,然后是 $ S^∗_c $ 被更新。在每个循环结束时, $ S_1 $ 被上一次循环中的最优解 $ S_p^ $ 取代, $ S_p^ $ 被 $ S_c^ $ 取代, $ S_c^* $ 被设置为随机解。一旦 $ S_1 $ 接近 $ S_2 $ ,就用随机解替换 $ S_2 $ ,以确保搜索的多样性。最后,返回在搜索过程中找到的最优解。
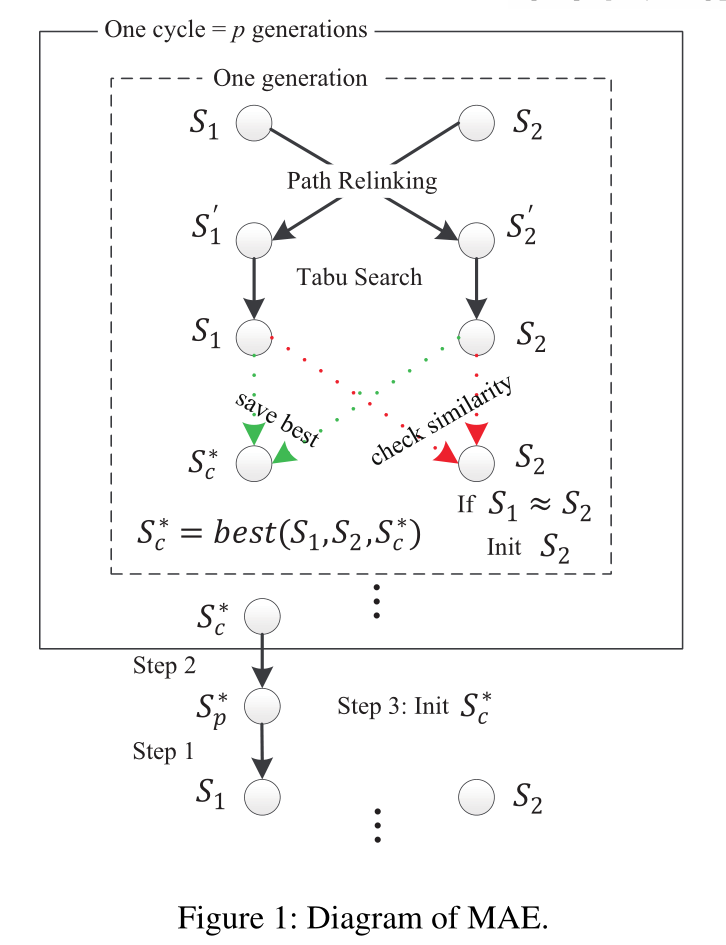
上一次循环的最优解 $ S_p^* $
本次循环的最优解 $ S_c^* $ ,刚开始的时候初始化为随机解
本次循环结束, $ S_1 = S_p^ $ ,被上一次循环的最优解取代。 $ S_p^ = S_c^ $ ,把最优解赋给 $ S_p^ $ 。? $ S_2 $ 咋办,重新生成一个随机解?,可能是新收一个徒弟。
2.2 Initial solutions and tabu search procedure
如同(González, Vela, and Varela 2015),MAE中FJSP的解决方案采取 $ (\alpha,\pi) $ 的形式,其中 $ \alpha $ 是每个操作 $ o $ 对机器 $ M_a \in M(o) $ 的可行分配,用 $ \alpha(o)=a $ 表示, $ \pi $ 是所有机器上的操作的处理顺序,与作业顺序兼容。开始时,MAE 使用 Init() 函数分别为 $ S_1 $ 、 $ S_2 $ 、 $ S^∗_c $ 、 $ S^∗_p $ 和 $ S^∗ $ 生成随机解决方案,在尊重所有约束条件的前提下,将每个作业的每个操作以相等的概率分配给其候选机器。
在MAE中调用Tabu搜索程序TS(S)来加强搜索。它通过将一个关键操作重新分配到不同的机器上并将其插入到一个可行的位置,或者通过改变同一机器上的关键操作的位置来改进解决方案S。请注意,关键路径中的操作被称为关键操作,关键路径是时间表的二分法图表示中最长的路径。在本文中,机器重新分配是在(Mastrolilli和Gambardella 2000)提出的k-insertion 邻域(这里称为 $ N^k $ )上进行的,而位置改变是在(González, Vela, and Varela 2015)提出的称为 $ N^\pi $ 的邻域上进行的。简而言之,MAE从 $ N^\pi\cup N^k $ 中反复选择最佳的非禁忌动作来执行,并且禁止在禁忌任期内再次执行该动作,这与(Peng, Lü, and Cheng 2015)中使用的禁忌策略类似。

2.3 Path relinking based recombination operator
两个个体 $ S_1 $ 和 $ S_2 $ 的传统路径重联包括找出个体 $ T_0 $ 、 $ T_1 $ 、 $ T_2 $ 、……,使 $ T_0=S_1 $ ,而 $ T_{i+1} $ 是通过对 $ T_i $ 进行一次移动得到的,并且比 $ T_i $ 更接近 $ S_2 $ 。在FJSP中应用路径重联的关键问题是定义两个个体之间的距离。
例如,在(González, Vela, and Varela 2015)提出的FJSP的散点搜索中,基于路径重联的重组算子被应用于两个从称为RefSet的集合中选出的解决方案 $ S_1 $ 和 $ S_2 $ ,使用两个距离。第一个距离 $ d^\alpha $ 是测量分配差异,定义为在 $ S_1 $ 和 $ S_2 $ 中具有不同机器分配的操作的数量,第二个距离 $ d^\pi $ 是测量序列差异,定义为需要同一机器的操作对以不同顺序处理的数量。此外, $ d^\alpha $ 的优先级比 $ d^\pi $ 高。为了从 $ T_i $ 获得 $ T_{i+1} $ ,同时考虑 $ d^\alpha $ 和 $ d^\pi $ 的距离。
在本文中,我们在 $ S_1 $ 和 $ S_2 $ 之间定义了一个独特的距离,它将分配差异和序列差异统一起来,具体如下。让 $ M^S_o $ ( $ P^S_o $ )表示解决方案S中分配给操作 $ o $ 的机器( $ o $ 在 $ M^S_o $ 上的位置), $ L^S_a $ 是解决方案 $ S $ 中分配给机器 $ a $ 的操作数。如果操作 $ o $ 在两个解决方案 $ S_1 $ 和 $ S_2 $ 中被分配到同一台机器上,我们定义 $ d_o(S_1, S_2) = |P^{S_1}_o - P^{S_2}_o| $ 为 $ o $ 在 $ S_1 $ 和 $ S_2 $ 之间的差异(见图2)。否则, $ o $ 可以被移到 $ M^{S_1}_o $ 的开头(结尾),然后从 $ S_1 $ 的 $ M^{S_2}_o $ 的开头(结尾)移到与 $ S_2 $ 的 $ M^{S_2}_o $ 中相同的位置(见图3中的路径1(路径2))。路径1和路径2之间的最小值被选为 $ S_1 $ 和 $ S_2 $ 之间的 $ o $ 之差,即 $ d_o(S_1,S_2) = \min \{P^{S_1}_o + P^{S_2}_o , (L^{S_1}_{M^{S_1}_o} - P^{S_1}_o) + (L^{S_2}_{M^{S_2}_o} - P^{S_2}_o)\} $ 。然后, $ S_1 $ 和 $ S_2 $ 之间的距离被定义为 $ d\left(S_{1}, S_{2}\right)=\sum_{i=1}^{n} \sum_{j=1}^{m} d_{o_{i j}}\left(S_{1}, S_{2}\right) $ 。
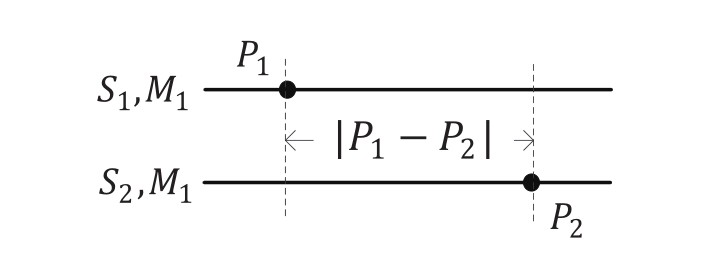
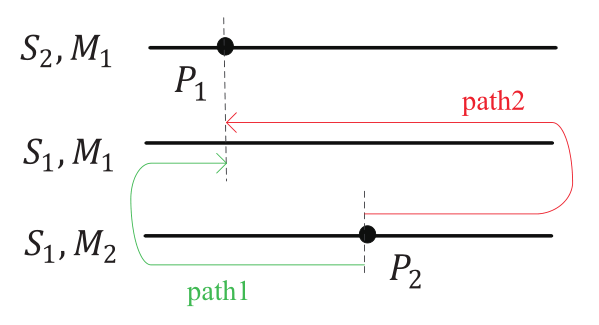
因此,为了从 $ T_i $ 获得 $ T_{i+1} $ ,我们的路径重联应用了一个单一的移动,即改变同一台机器上的操作的位置,或者将不同的机器重新分配给一个操作,这样得到的解决方案是可行的,并且比 $ T_i $ 更接近 $ S_2 $ 。请注意,被移动的操作可以是非关键性的。我们的邻域实际上是 $ N^\pi_g\cup N^k_g $ ,其中 $ N^\pi_g(N^k_g) $ 是由 $ N^\pi(N^k) $ 扩展而来,包括非关键操作的移动,导致可行的解决方案。由于有唯一的距离,这种路径重新连接要简单得多。

算法2介绍了我们基于路径重联的重组算子。该运算符使用三个参数 $ \alpha $ 、 $ \beta $ 和 $ \gamma $ ,其值将在以后根据经验确定。从初始解 $ S_i $ 到指导解 $ S_g $ 的路径是按以下步骤建立的。设 $ S_c $ 为当前解( $ S_c $ 被初始化为 $ S_i $ )。首先,我们构建一个可行的解决方案 $ N $ 的集合,这些解决方案可以通过应用一个单一的动作从 $ S_c $ 得到(第5-13行)。对于每个操作 $ o $ ,如果 $ o $ 在 $ S_c $ 和 $ S_g $ 的不同机器上,让 $ N^k_g(S_c, o) $ 是通过将 $ o $ 移动到 $ S_g $ 中 $ o $ 的机器上而从 $ S_c $ 获得的可行解决方案的集合。否则,让 $ N^π_g(S_c,o) $ 是通过改变 $ o $ 在同一台机器上的位置从 $ S_c $ 得到的可行方案的集合。让 $ S_{min} $ 是使 $ d_o(S_{min}, S_g) $ 最小的解决方案(并列关系是随机打破的)。然后, $ N^k_g(S_c,o) $ 或 $ N^π_g(S_c,o) $ 中的 $ S_{min} $ 被添加到 $ N $ 中。第二,从N中移除每一个 $ d(S, S_g)>d(S_c, S_g) $ 的解决方案 $ S $ ,并估计每个剩余解决方案的makespan(第14-18行)。第三,对于N中剩下的每个解决方案S,计算出更接近 $ S_g $ (具有更好的makespan)的解决方案的数量,并用indexDis(S)(indexObj(S))表示。(第21-24行)。第四,我们按照indexDis(S)+indexObj(S)的递增顺序对 $ N $ 进行排序,并随机选择前 $ \gamma $ 个解决方案中的一个作为路径上的下一个 $ S_c $ ,如果它与 $ S_g $ 的距离小于 $ \beta \times d(S_i, S_g) $ ,则将其存入PathSet(第25-30行)。这些步骤重复进行,直到 $ d(S_c, S_g) $ 不再大于 $ \alpha \times d(S_i, S_g) $ (第4行)。最后,PathSet中的最佳解被返回作为参考解(第32行)。
很明显,集合N的最大尺寸是 $ n_o $ ,其中 $ n_o $ 是所有工作中的所有操作总数,即 $ n_{o}=\sum_{j=1}^{n} n_{j} $ 。第5-13行的最差时间复杂度是O(n2o)。第21-25行实际上是对集合N的解进行排序,其时间复杂度为 $ O(|N|\log|N|) $ 。因此,算法2的最差时间复杂度是 $ O(n^3_o) $ 。
三、Computational Results Experimental protocol and benchmarks
我们的MAE算法在C++中实现,并运行在英特尔Xeon E5-2697处理器上,具有2.60 GHz CPU和2 GB RAM。在我们的实验中,我们将p、α、β、γ分别设置为10、0.4、0.6和5。当在同一台机器上具有不同机器分配或不同位置的操作数小于所有作业中操作总数的10%时,两个解决方案被认为是接近的,其中一个解决方案被替换为随机解决方案。禁忌搜索过程的最大迭代次数为10000次。这些参数值是通过大量的初步实验确定的。
我们在文献中广泛使用的四个基准上评估了MAE的性能:DPdata(Dauzère-Pérès和Paulli 1997)、BCdata(Barnes和Chambers 1998)、BRdata(Brandimarte 1993)和HUdata(Hurink、Jurisch和Thole 1994),共有313个不同大小和灵活性的实例。MAE应用于每个实例,有20次独立运行。按照该领域的常规做法,我们使用以下数值来比较不同的方法:
- 20次运行期间目标的平均相对百分比偏差 RPD,定义为 $ RPD=100 \times(f−LB)/LB $ ,其中 f 是通过给定算法获得的最大完工时间,LB是 $ \text{Quintiq}^1 $ 中提供的下限;
- 以及20次运行的平均计算时间t(s),以秒为单位。
为了与其他算法进行公平比较,BRdata和BCdata实例的MAE截止时间设置为90秒,DPdata和HUdata实例的MAE截止时间设置为5分钟,这与GRASP-mELS中的相同。我们还提供了截止时间为1小时的MAE结果。此外,我们将计算时间标准化为与计算机无关的CPU时间(CI-CPU),方法与GRASP-mELS中的方法相同。因此,将计算机的速度系数设置为1,GRAP-mELS、SSPR、HA和HGTS的速度系数分别为1.09、0.75、0.50和0.63。
3.1 Comparison with metaheuristics
在四个基准集上,我们将MAE算法与最新的最新算法(SSPR、HGTS、HA和GRASP mELS)进行比较。比较结果见表1-4。请注意,列best(avg)和t(s)是获得的最佳(平均)解,以及每个算法所需的平均计算时间(以秒为单位),LB值标记为∗ 表示最优解,每个参考算法可以获得的最知名解用粗体表示。行#better、#even和#better给出了MAE在5分钟或90秒内获得的最佳解比每种参考算法更好、相等和更差的实例数。
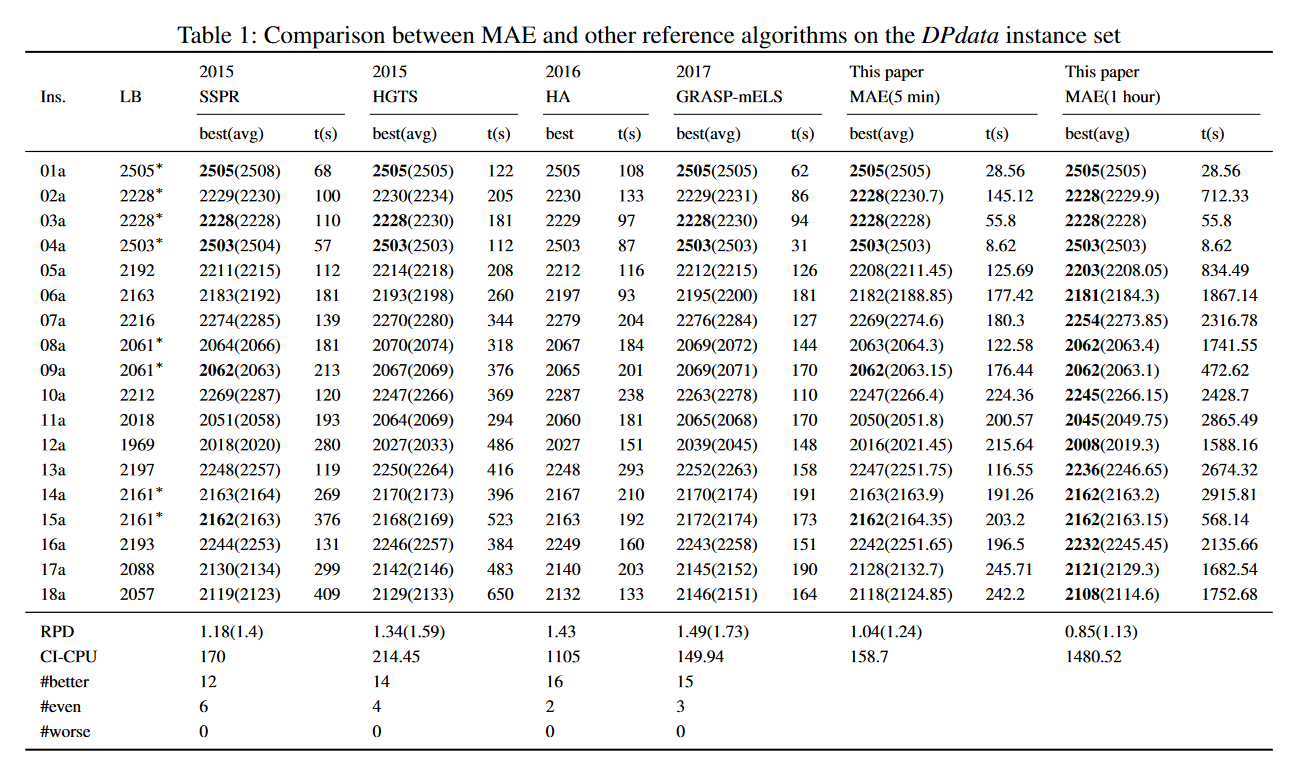
从表1可以看出,在DPdata基准上,MAE在解决方案质量和计算时间方面都优于HGTS和HA。尽管与SSPR和GRASPmELS相比,MAE需要稍多的计算时间,但对于最佳和平均目标值,其RP D值最少(1.04和1.24)。此外,MAE在12例和15例中分别比SSPR和GRAP mELS获得更好的结果。当将截止时间延长到1小时时,MAE对15个实例改进了以前最著名的解决方案。
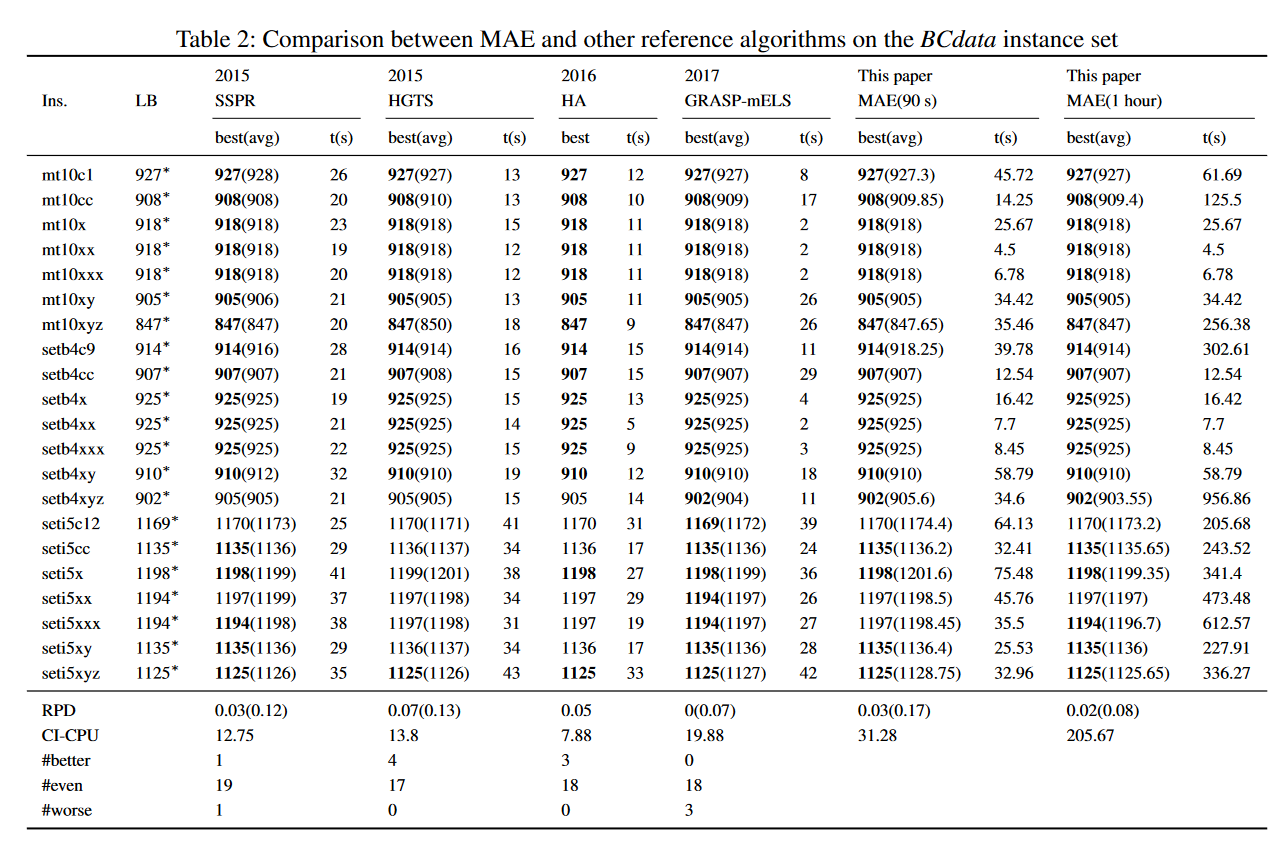
从表2可以看出,MAE在BCdata基准上与HGTS和HA具有竞争力,因为它的最佳和平均目标值较小。此外,MAE在解决方案质量方面优于HGTS。与SSPR相比,MAE分别在1、19和1个实例中获得更好、相等和更差的解。GRASPmELS在BCdata基准上的性能优于MAE。
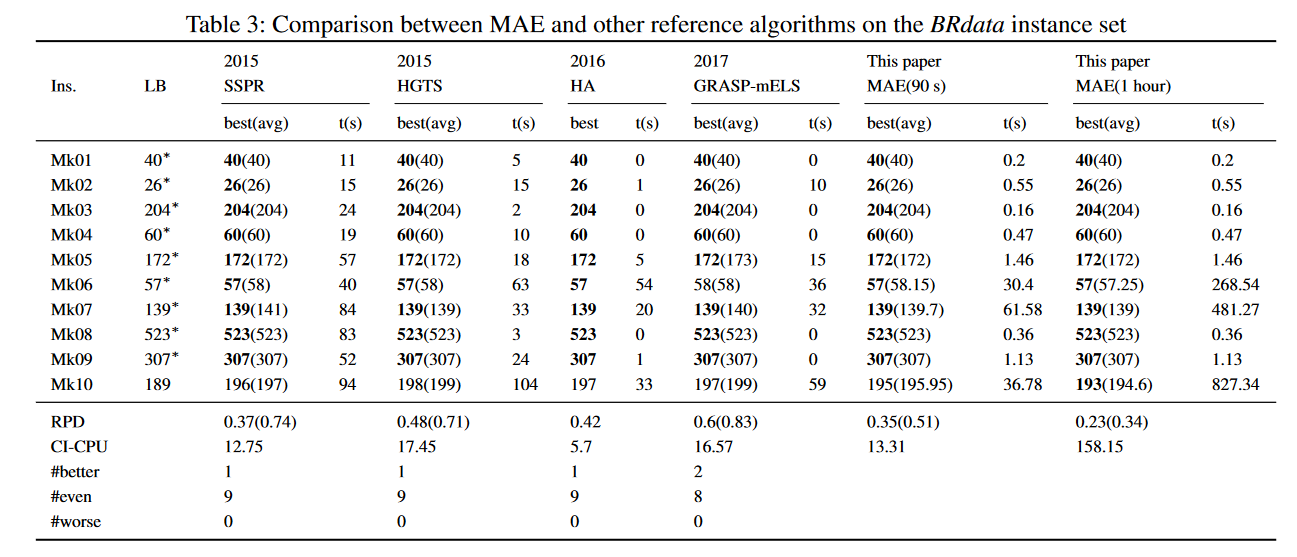
表3中的结果表明,MAE在解决方案质量和计算时间方面都优于SSPR、HGTS和GRAP mELS。虽然HA所需的计算时间稍短,但MAE的最佳和平均完工时间值较小。此外,与其他参考算法相比,MAE在所有情况下都获得了更好或相同的结果。
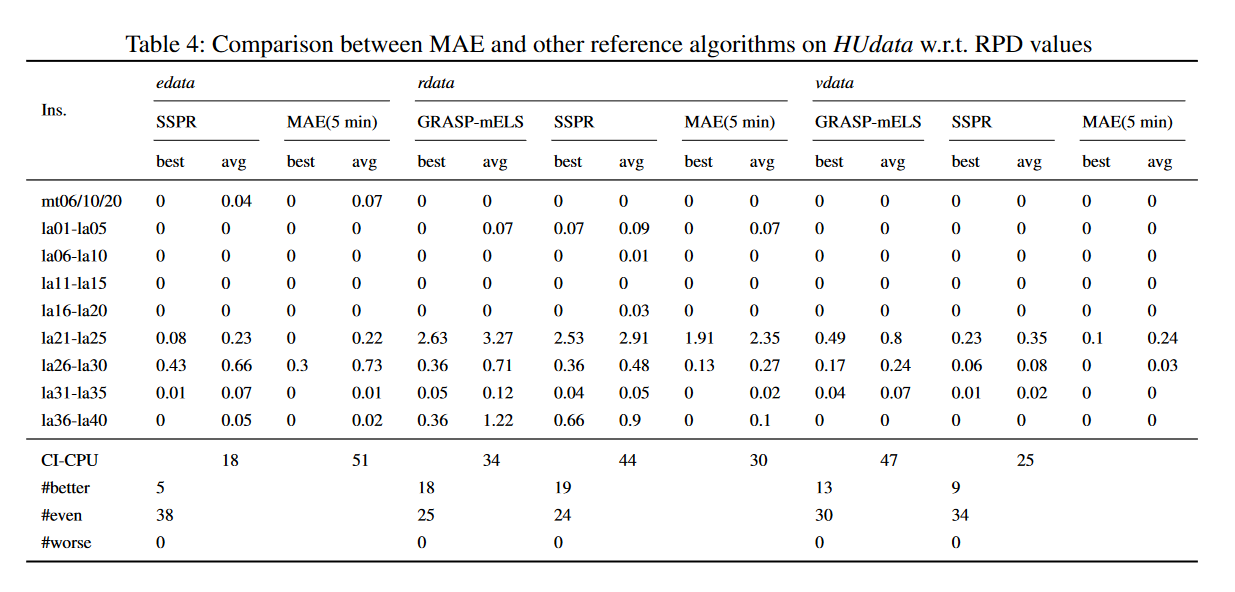
表4给出了在HUdata基准上MAE与SSPR和GRAP mELS的比较结果。人们观察到,MAE的性能优于SSPR和GRAP mELS,因为MAE在所有实例中都能获得更好或相等的结果,并且只需要较少的计算时间,rdata集上的GRAP mELS除外。特别是,MAE分别对edata、rdata和vdata上的4(5)、18(19)和13(9)个实例改进了GRAP mELS(SSPR)获得的最佳结果。
总之,MAE改进了SSPR和GRASP mELS之前获得的最佳结果,在178个测试实例中,分别有47个和52个。
3.2 Comparison with the state-of-the-art exact method
我们将MAE与基于约束编程的最新精确方法进行了比较:LNS+FDS(Viĺım、Laborie和Shaw,2015)。LNS+FDS构成了CP Optimizer中自动搜索调度问题的基础,CP Optimizer是IBM ILOG CPLEX Optimization Studio的一部分。LNS+FDS(也称为CPO)已在一系列调度基准上成功测试,如JSP和FJSP等。
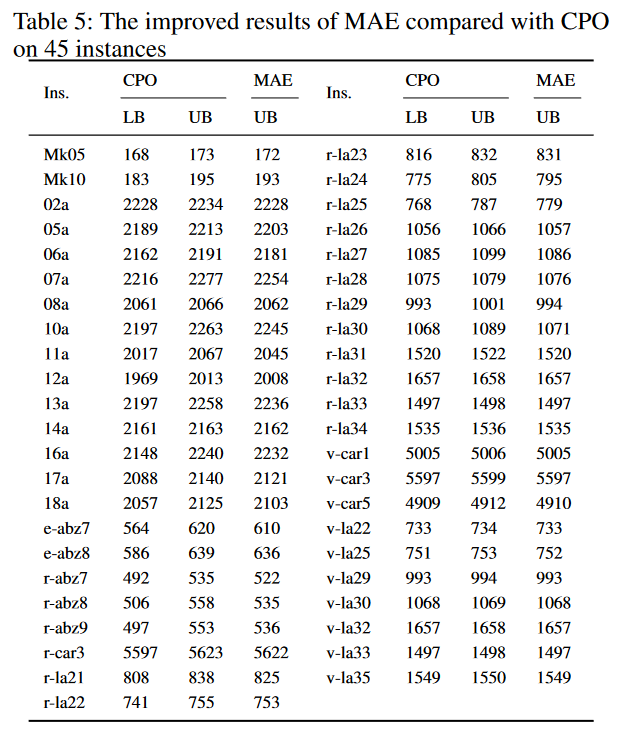
与313例中的CPO相比,MAE分别在45例、255例和13例中获得更好、相等和更差的结果。表5报告了45个改进实例的MAE结果以及与CPO的比较。请注意,CPO的结果是在8小时的时限内获得的,而MAE的结果是在1小时的时限内获得的。
3.3 Comparison with the industrial solver Quintiq
我们现在将MAE与著名的工业求解器Quintiq进行比较,Quintiq为313个实例中的119个实例找到了新的最知名的解决方案。它还指出了所有313个实例的解决方案质量的世界记录,以及第一个创下记录的方法。然而,Quintiq并没有描述他们的方法和获得这些结果的时间限制。
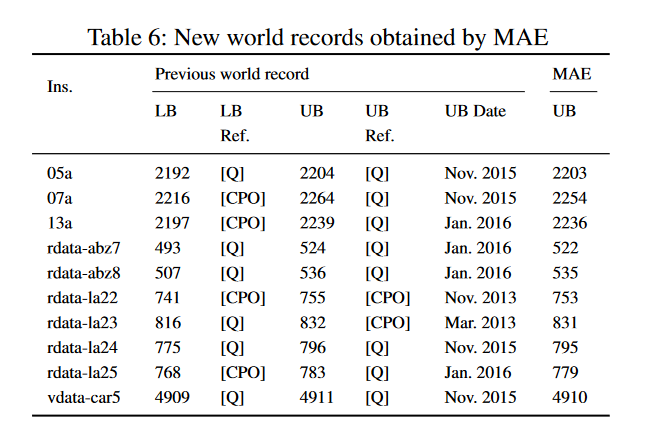
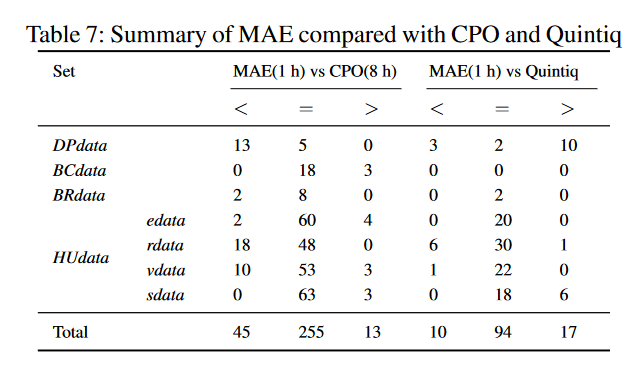
我们通过对MAE使用1小时的时间限制来比较MAE和Quintiq。实验表明,在121个实例中,MAE获得的结果比Quintiq更好。表6中提供了这些由MAE获得的新记录,供以后比较,其中 “UB Ref. “和 “UB Date “栏分别代表获得新记录的方法和日期,”[Q]”代表Quintiq方法。最后,表7报告了MAE与CPO和Quintiq的总结性比较,其中列<、=、>表示MAE获得比参考算法更好、相同和更差结果的实例数。
3.4 Discuss and analysis
为了显示基于两个个体的进化框架的优点,我们将MAE与被称为迭代塔布搜索(ITS)的轨迹方法进行了比较,该方法在单一解决方案上工作。在ITS的每个迭代中,执行与MAE相同的Tabu搜索程序,然后是一个扰动程序,在N π ∪ N k中随机对当前的解决方案或最佳发现的解决方案应用0.2 ∗ |Nc|移动,如果连续非改进的迭代次数超过500,其中Nc是关键操作的集合。
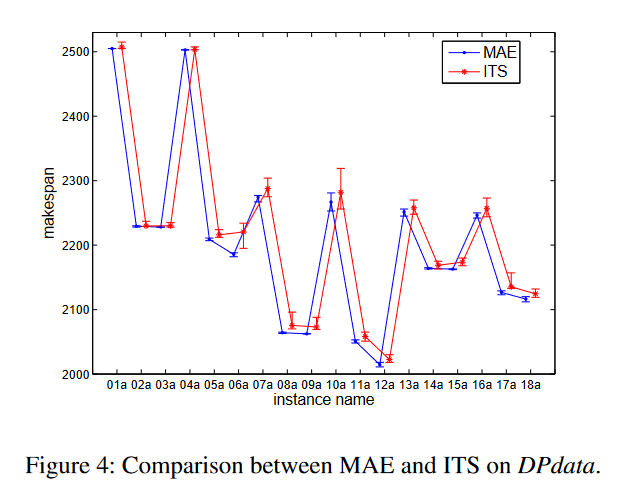
图4显示了MAE和ITS针对DPdata中18个实例中的每一个获得的最佳、平均和最差解。可以观察到,在所有情况下,MAE的最佳、平均和最差解都优于或等于ITS的最佳、平均和最差解。此外,MAE的最佳和最差解之间的差异也小于ITS的差异。这表明基于两个个体的进化算法优于轨迹法。
在初步实验中,我们选取了11个不同的p值(5,6,…,15),5组不同的[α,β]值([0,0.2],…,[0.8,1]),以及10个不同的γ值(1,…,10)来分析参数敏感性。所有参数总共有11510=550个组合。我们独立运行MAE 10次,以解决BCdata中一个相对困难的实例seti5xyz,每次运行的截止时间为90秒。结果表明,考虑到解的质量和计算效率,当p、α、β和γ分别设置为10、0.4、0.6和5时,MAE的性能最佳。在下面的段落中,我们将通过扩展MAE的值域和保持其他参数不变,进一步分析一个参数对MAE性能的影响。
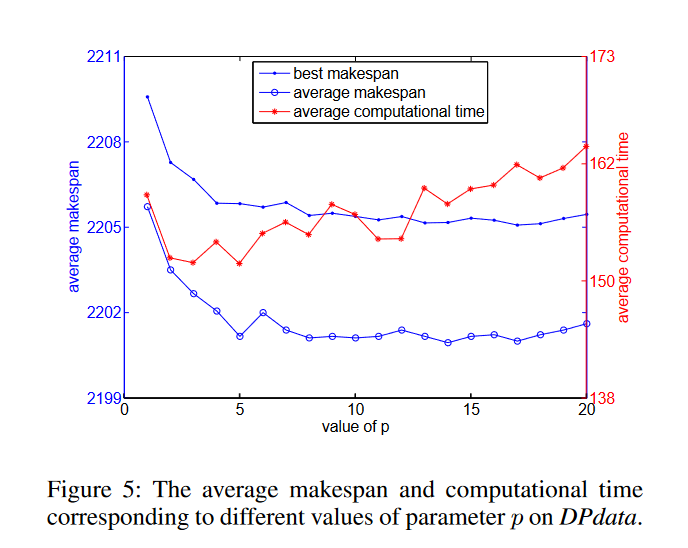
为了分析参数p对MAE性能的影响,我们取了20个不同的值(p∈ {1,…,20}),保持其他参数不变,并对DPdata中的所有实例应用MAE。相应的结果如图5所示。人们发现,当p∈ {1,…,10}并在p∈ {10,…,20},而当p∈ {1,2,3}并随着p∈ {3, . . . , 20} . 原因可能在于,当p很小时,在上一个周期中保存的最佳解决方案不是高质量的,这无法提供好的可继承特性。当p太大时,一个循环中的最佳解更接近迄今为止找到的最佳解,这无法提供足够的多样性,因此MAE更有可能陷入局部最优。MAE中p的最佳值建议为10。
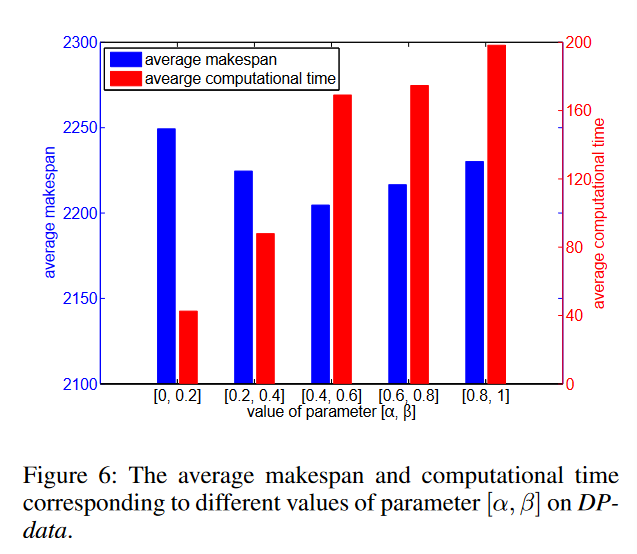
为了分析参数α、β、γ对MAE的影响,我们对[α、β]、[0.2]、[0.8,1])取5组值([0,0.2]、[0.8,1]),对γ取15组值(1,…,15),保持其他参数不变,并分别对DPdata和BCdata进行实验。结果如图6和图7所示。图6显示,平均完工时间从第一组到第三组减少,从第三组到第五组增加,而相应的计算时间在整个范围内逐渐增加。图7显示,当γ∈ {1,…,5}并且当γ∈ {5, . . . , 15}. 考虑到解的质量和计算效率,建议α、β和γ分别为0.4、0.6和5。
MAE是有效的,因为它使用两个个体S1和S2在集约化和多样化之间保持了良好的平衡,其中S1扮演集约化的角色,S2扮演多样化的角色。为了说明这一点,我们在图8中描述了在解决代表性实例01a时,S1和S∗的目标值的演变,以及距离d(S1, S∗)和d(S1, S2)。我们看到,S1的目标值通常是好的,而S∗的目标值是单调的。这是可能的,因为d(S1, S2)周期性地变大(与d(S1, S∗)相比),所以S1和S2的路径重联算子能够找到多样化的解决方案。

此外,我们对MAE与SSPR和GRASPmELS相比,通过多次运行得到的实例的平均makespan进行了统计学意义上的检验,得出的MAE和SSPR(GRASP-mELS)之间的平均makespan的p值见表8。考虑到0.05的显著性水平,从表8中可以看出,MAE和SSPR在DPdata、rdata和vdata上有显著差异,而MAE和SSPR在BCdata、BRdata和edata上没有显著差异。此外,在DPdata、rdata、vdata和BCdata上,MAE和GRASP-mELS之间有显著差异,而在BRdata和edata上,MAE和GRASP-mELS之间没有显著差异。原因可能在于BCdata、BRdata和edata的实例相对容易解决。表1-4中的#better、#even和#worse的值也可以说明实例的难度。
四、Conclusion
我们提出了一种称为MAE的师徒进化算法来解决柔性作业车间调度问题,该算法在三个主要方面与基于单一解决方案和传统基于种群的元启发式算法有所不同:(1)MAE中的种群规模是两个,允许两个个体之间进行有效协作;(2) MAE使用简单但非常有效的个体更新策略来确保进化的质量和多样性;(3) 为了产生有希望的后代解决方案,MAE使用了一种基于路径重新链接的语义问题特定重组算子,并为两个个体定义了一种新的距离定义。计算实验表明,MAE在求解质量和计算效率方面都有很高的性能。我们坚信,这种基于两个个体的主学徒进化算法是解决其他具有挑战性的组合优化问题的一个有前途的框架。