Luobuyu's Blog

0%

海量稀疏图中最小顶点覆盖的动态阈值搜索

发表于 分类于 ， 热度： ℃ 评论：
本文字数： 7.7k 阅读时长 ≈ 7 分钟
海量稀疏图中快速找到最小顶点覆盖。

海量稀疏图中最小顶点覆盖的动态阈值搜索

摘要：

许多与复杂网络分析相关的重要应用需要在海量图中找到小顶点覆盖。本文提出了一种有效的随机局部搜索算法 DTS_MVC 来完成这一任务。依靠基于顶点的快速搜索策略，DTS_MVC通过在阈值搜索阶段和条件改进阶段之间交替进行有效地探索了搜索空间。

阈值搜索阶段：该算法接受改进和非改进的解决方案，这些解决方案满足动态变化的质量阈值。

条件改进阶段：只接受改进的解决方案。

引入了一种新型的非参数操作机制，以避免搜索循环。在86个大型现实世界基准图上进行的计算实验表明，通过发现7个改进的最著名结果（新的上限），DTS_MVC的性能非常出色。进行其他实验以阐明DTS_MVC的关键成分。

关键词：

顶点覆盖、低复杂性启发式算法、海量稀疏图

一、介绍

给定一个连通无向图 $ G = (V,E) $ 使用顶点集 $ 𝑉 $ 和边集 $ 𝐸 $ , 图 $ G $ 的顶点覆盖 $ 𝑆 $ 是 $ V $ 的子集 $ (𝑆 \subset 𝑉) $ ，图中的每条边至少有一个顶点属于 $ S $ 。最小顶点覆盖（MVC）问题是确定最小基数的顶点覆盖。MVC问题等价于最大独立集（MIS）问题和最大团问题（MC）。因为给出图 $ G $ 的最小顶点覆盖 $ S $ ，那么 $ V\setminus S $ 就是图 $ G $ 的最大独立集，补图 $ \bar{G} $ 的最大团。除了许多常规应用之外，MVC及其等效模型在社会网络分析（Fortunato，2010）、生物信息学（Matsunaga et al.，2009）和经济学（Boginski et al.，2005；Wu和Hao，2015b）等重要领域也越来越受欢迎。

独立集：给一无向图，找出一个点集，使得任意两点之间都没有连边，这个点集就是独立集。而点最多的独立集，就是最大独立集。

团：对应地，任意两点之间都有边，我们称之为团。同时也有最大团。

定理：无向图的最大团等于其补图的最大独立集，等于顶点数减去补图的最小顶点覆盖。

顶点覆盖：任意一条边都至少有一个顶点落入顶点覆盖中。反面是剩下的点都没有连边，就是独立集。

最小顶点覆盖的反面是最大独立集。

二分图中最小顶点覆盖等于最大匹配

考虑到MVC的决策版本是NP完全的，在一般情况下求解MVC在计算上具有挑战性（Garey和Johnson，1979）。由于其NP困难性，大多数以前的MVC算法采用随机局部搜索（SLS）启发式（例如，Cai等人，2010、2013、2015；Shyu等人，2004；Richter等人，2007；Pullan，2009），以在合理的时间内寻求高质量的次优解。对于等效MC问题，还提出了几种基于一般分枝定界法的精确算法（例如，San Segundo et al.，2011；Li and Quan，2010；Östergård，2002；Tomita and Kameda，2007）。这些以前的算法被证明可以有效地从小型或中型的DIMACS和BHOSLIB基准集中求解传统图。

与此同时，互联网的快速增长和信息技术的最新进展产生了大量数据，这些数据的底层图表远远大于传统的基准。这些真实世界的图（如社交网络）通常是巨大的，有数千万个顶点，并且稀疏，边缘密度低，其中顶点的度数通常遵循幂律分布（Newman，2003）。这些庞大的图表对现有的解决方案方法构成了严重挑战（Pardalos和Rebennack，2010）。首先，由于图的矩阵表示，许多现有算法实现无法应用（Verma et al.，2015）。使用矩阵表示法，具有数百万个顶点的图形无法加载到计算机的工作内存中。其次，许多性能最好的SLS算法在尺度相关候选集上采用最佳改进（或基于算子）搜索策略进行解转换（例如，Pullan和Hoos，2006；Cai等人，2013；Jin和Hao，2015；Wu和Hao，2013）（见第3.3节）。这种策略会导致每次迭代算法的时间复杂度很高，并且在海量图上变得无效和不切实际。事实上，在设置海量图时，此策略的每次应用都需要数百万次评估操作，即使非常简单，也必然会导致计算效率非常低，并降低算法的速度。

近年来，为大规模图上的MVC及其等价问题开发合适的算法受到了越来越多的研究关注。Pattabiraman et al.（2013、2015）、Verma et al.（2015）和San Segundo et al.（2016）提出了精确算法，以优化求解等效MC。另一方面，由于大量稀疏图的大小和所考虑问题的难处理性，SLS代表了一种寻找高质量近似解的自然解决方法，但需要结合专门的设计才能有效。Abello等人（1999年）为MC引入了GRASP启发式算法，该算法集成了图分解方案和外部存储过程。有人注意到，将MC算法应用于MVC需要对高度密集和大量的补码图进行操作，这使得该算法不适合于解决MVC。最近，引入了一种称为FastVC的专用SLS算法，用于在海量图中查找小顶点颜色（Cai，2015），该算法基于NuMVC算法（Cai et al.，2013），包括用于初始解生成和解转换的特定启发式算法。另一种新的SLS算法LinCom（Fan等人，2015）采用了与FastVC相同的算法方案。LinCom通过集成用于解决方案初始化的简化规则和采用有效的数据结构来实现最佳改进启发式，从而将自己与FastVC区分开来。LinCom被证明能够在大量真实图形上与FastVC展开竞争。据我们所知，FastVC和LinCom是目前针对本工作中考虑的MVC问题性能最好的启发式算法，并将作为评估我们提出的算法的主要参考。

除了上述关于MVC的研究外，我们注意到一些最近致力于扩展基本MVC和派系模型的努力，例如具有不确定边缘失效的稳健派系问题（Yezerska et al.，2018），派系松弛问题（k-blocks和k-robust 2-clubs，Balasubramaniam和Butenko，2017），基于度的准派系问题（Pastukhov et al.，2018），最大准集团问题（Pinto等人，2018年）、最大s丛问题（Gao等人，2018年；Zhou和Hao，2017年）、最大平衡双液问题（Wang等人，2018年；Zhou和Hao，2018年）和最大诱导双液问题（Shahinpour等人，2017年）。这些扩展模型与经典的MVC和clique模型一起，为建模和分析海量图和复杂网络提供了有用的相关手段。设计能够有效处理海量图的这些问题的新方法是一个真正的兴趣，也是一个巨大的挑战。

在这项工作中，我们致力于解决大规模稀疏图上的MVC问题，并引入了一种快速有效的SLS启发式算法DTS_MVC（动态阈值搜索MVC）。DTS_MVC基本上在阈值搜索阶段和条件改进阶段交替进行，前者接受新的（改进的或非改进的）解决方案，后者受动态演化的质量阈值的约束，后者只寻求改进的解决方案。DTS_MVC的原始特性和这项工作的贡献如下所示。

  • 首先，DTS_MVC使用基于顶点度信息的随机贪婪过程来构建其初始解（顶点覆盖）。具有相同的复杂性 ( $ 𝑂(|𝐸|) $ ) 作为传统的随机构造过程，贪婪过程能够生成质量更好的初始解，有助于加快DTS_MVC的搜索过程。

    使用的贪婪算法生成初始解，复杂度和随机构造一样，但是生成的解的质量更好

  • 其次，阈值搜索阶段采用基于顶点的策略和无参数操作禁止机制进行解变换。基于顶点的策略将从一个小的候选算子集中提取的最佳算子应用于给定的顶点（随机选择），以变换现有解。从计算的角度来看，这种方法比传统的基于算子的策略要有效得多。传统的基于算子的策略需要在一个大的候选顶点集中确定应用给定变换算子的最佳顶点。

    随机选择的一个顶点，选择最佳的算子

    传统的方式是选择一个算子，找最佳顶点

  • 第三，DTS_MVC使用随机“开关”控制每个阈值搜索阶段的输入，该阶段要么是爬山改进阶段的局部最优值，要么是最后一轮阈值搜索返回的解。这种设计自然地加强了搜索过程的强化和多样化之间的平衡。

  • 第四，对86个海量真实图形的计算评估表明，DTS_MVC通过改进7个并匹配64个最著名的结果，与两个致力于海量图形的最先进MVC解决方案（FastVC和LinCom）进行了对比。

  • 最后，所提出的基于顶点的策略和操作禁止机制本质上是独立于问题的，可以有利地用于设计其他图问题的搜索算法。考虑到这些技术有助于加速搜索过程和简化算法过程，当问题规模较大且允许的计算时间有限时，它们将特别有用和有前途

论文的其余部分组织如下。在介绍了初步定义和符号（第2节）之后，我们将在第3节中描述所提出的算法及其组成部分。在第4节中，我们给出了计算结果，并与最先进的方法进行了比较，并分析了关键的算法组件。在最后一节中，我们得出结论，并对未来的研究提出一些想法。

二、基本定义和符号

给出一个图 $ G(V,E) $ ：

  • $ N(v) = \{u \in V:(u,v)\in E\} $ 表示 $ v $ 的邻居节点。
  • $ deg(v) $ 表示节点 $ v $ 的度。
  • $ avgDeg = \sum_{v\in V} deg(v)/n $ 表示图 $ G $ 的平均度。

使用 $ S $ 表示解，定义以下变量用于算法表述：

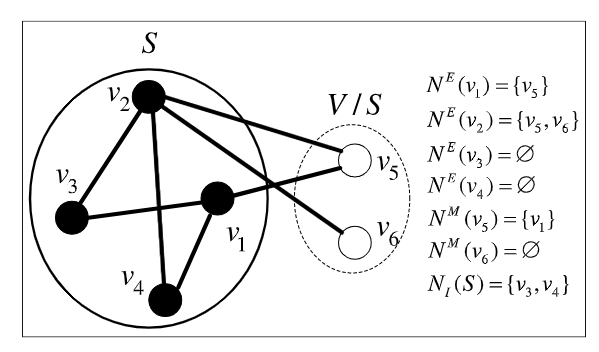
  • 扩展邻域 $ N^E(v) $ 表示 $ (u,v) $ ，其中 $ v \in S, u \in V \setminus S $ ，就是非解中的邻居节点。
  • 映射邻域 $ N^M(v) $ 表示 $ v \in V \setminus S $ ， $ N^M(v) = \{u \in S : (u,v)\in E,|N^E(u) = 1|\} $ 。即表示 $ v $ 是解中点 $ u $ 的唯一一个非解邻居节点。
  • 提升邻域 $ N_I(S) = \{v \in S : |N^E(v)| = 0\} $ 也就是 $ v $ 不存在非解邻居节点，只存在解内部的边。那么可以直接把 $ N_I(S) $ 中的点删除，可以得到一个更好的解。

image-20220702165155555

三、DTS_MVC算法

3.1 框架

首先使用 贪心构造算法 生成一个初始解。然后在阈值搜索阶段和条件改进阶段之间交替进行，找到更优的解。

image-20220703104351006

阈值搜索阶段：

使用基于顶点的策略。按照随机顺序扫描所有顶点，针对每个顶点从三种算子 DROP、ADD、SWAP中选择一种算子或者直接执行移动操作。

DROP从解中删除顶点，ADD将顶点加入解中

确切地说，在挑选出一个顶点后，该算法以特定的顺序检查两个相关的运算符（{DROP, SWAP}或{SWAP, ADD}，取决于该顶点是在当前顶点覆盖范围内还是在范围外）（确保最合适的运算符总是首先被应用），任何产生的满足质量阈值的相邻解决方案都被立即接受。

通过一种响应机制，质量阈值随着搜索过程中找到的最佳解而动态演变。这种基于顶点的快速策略有助于算法有效地访问大量解决方案，以进行给定的搜索工作。在这一阶段，该算法还使用操作禁止机制（无参数禁忌列表（Glover和Laguna，2013））来避免反转最近执行的动作。当所有顶点位于 $ 𝑉 $ 只检查过一次。由于基于顶点的策略和操作禁止机制，搜索过程有望探索搜索空间的各个区域，而不容易陷入局部最优。

使用了禁忌策略

作为阈值搜索阶段的补充，DTS_MVC 在条件改进阶段执行严格的爬山策略，以加强搜索（算法1的第28-39行）。爬山过程收缩当前顶点覆盖 $ 𝑆 $ ， 通过删除所有未连接到 $ 𝑉\setminus 𝑆 $ 的顶点。 该阶段被称为“条件”阶段，因为只有当随机开关（“开”或“关”）为“开”时，才接受爬山过程的局部最优解成为下一轮阈值搜索的起始解。

DTS_MVC迭代以上两个阶段，以寻求越来越更好的解决方案，直到达到算法的截止时间为止。在接下来的内容中，我们介绍了DTS_MVC算法的三个主要组成部分：贪婪构造过程，阈值搜索阶段和条件改进阶段。

3.2 贪婪构造过程

贪婪构造算法在时间复杂度和解的质量之间达到了平衡性。

贪心构造使用顶点的度作为启发式信息来构造解，有利于从当前解中派出度比较小的顶点。这种启发式背后的思想是，具有较小度数的顶点不太可能相互连接（他们比较可能连接的是其他顶点，没有相互进行连接），因此可能可以从解中排除更多此类顶点。

从包括所有顶点的解开始，贪心构造通过每次删除 $ N_I(S) $ 中的一个顶点，迭代收缩解的大小，直到 $ N_I(S) $ 为空。

image-20220703104526713

确定将顶点 $ u $ 从 $ S $ 中删除，根据 avgDeg 和 $ N_I(S) $ 的大小之间的关系分为两种情况。如果 avgDeg 小于 $ |N_I(S)| $ 则从 $ N_I(S) $ 中随机选择 avgDeg 个节点， $ u $ 为其中度数最小的节点；否则选择 $ N_I(S) $ 中度数最小的节点。

定理1： 贪心构造算法的时间复杂度为 $ O(m) $

证明： 略

3.3 阈值搜索阶段

在阈值搜索阶段（算法1的第8-27行），通过组合使用三种不同的基本算子（DROP、ADD和SWAP），可以接受改进和非改进解。DROP将顶点踢出当前顶点覆盖；ADD添加通过包含新顶点来扩展当前顶点覆盖；SWAP交换顶点 $ 𝑣 $ 和 $ 𝑢 $ 。我们注意到，通过参考解质量阈值接受非改进解的思路来自于阈值搜索（Dueck和Scheuer，1990）。该阶段的主要创新包括基于顶点的探索策略和非参数操作禁止机制，其工作原理及其对问题解决的贡献详述如下。

以前用于MVC及其等价问题的SLS算法通常采用基于算子的策略，并结合最佳改进启发式（Jin和Hao，2015；Pullan和Hoos，2006；Cai等人，2013），其操作如下。给定当前解，该算法将变换算子应用于从顶点候选集中选择的最佳元素（顶点），该顶点候选集的大小与 $ 𝐺 $ 相关，并且随着问题规模的增加而增加。从这样的顶点候选集中识别最佳顶点需要大量比较操作，这非常耗时。尽管基于算子的策略适用于中小型图（多达数千个顶点），但它对于海量数据集来说是不可接受的。

与之前的方法不同，我们在阈值搜索阶段引入了一种低复杂度的搜索机制。DTS_MVC采用基于顶点的策略，对于给定顶点，从候选算子集中选择最优的算子对该顶点进行操作，而不是而不是为一个算子寻找最佳顶点。由于候选算子集很小（在我们的例子中，一个顶点只有两个可能的算子），并且与问题大小无关，因此该策略是有效的。基于顶点的策略的思想符合一种常见的直觉，即在大规模问题的SLS算法的背景下，最好执行许多相对简单但有效可计算的搜索步骤，而不是少数复杂的搜索步骤（Hoos和Stützle，2004）。由于基于顶点的策略，DTS_MVC能够访问许多不同的解决方案，并探索搜索空间的各个区域，以定位高质量的解决方案。

SLS算法的一个重要问题是防止搜索重新访问以前访问过的解决方案。为了解决这个问题，我们在阈值搜索阶段设计了一种新的非参数操作禁止（OP）机制。该机制的关键思想是确保适用于顶点的操作在一轮阈值搜索中最多应用一次。很明显，对于DROP和ADD，这个条件总是满足的。因此，OP机制用于确保对顶点的swap操作(𝑣,𝑢) 最多应用一次。

$ v $ 移除， $ u $ 移入。设置禁忌期

对每一个节点 $ u $ 设置一个 AGE 计数器，每次将 $ u $ 换入时，设置 $ AGE_u = round $ 。表示 $ u $ 十当前轮次新增的，不用管，避免在该轮次中移出来。只有 $ AGE < round $ 的结点才可以进行 swap 操作。OP机制与每轮阈值搜索之前所有顶点的随机排列相结合（算法1的第7行），可以被视为一种无参数禁忌机制，每个执行的操作都具有随机禁忌保留期（Glover和Laguna，2013）。我们的经验表明，所有顶点的随机排列是一个重要的操作，极大地提高了DTS_MVC的性能。

DTS_MVC的阈值搜索阶段基于三种基本的移动算子，结合基于顶点的策略和操作禁止机制，对搜索空间进行平衡检查。对于该阶段的每一轮，该算法首先随机洗牌所有顶点 $ 𝑉 $ ，然后逐个访问顶点。对于每个顶点 $ 𝑣 $ 考虑到这一点，我们根据顶点是在顶点覆盖内还是在顶点覆盖外来定义其算子候选集𝑆.

情况1：如果 $ v \in S $ ，候选算子为DROP和SWAP。先使用DROP，因为DROP可以提高解的质量，SWAP对解的质量没有改变。如果二者都不能执行，算法就跳过节点 $ v $ 。

DROP算子使用情形：如果 $ v $ 的扩展邻域是空集，可以使用DROP（例如 $ v \in N_I(S) $ ）。

SWAP算子使用情形：（同时满足）

  • $ v $ 未在本 round 参与 SWAP 操作
  • $ v $ 只连接到 $ V \setminus S $ 中的一个节点（即 $ |N^E(v)| = 1 $ ，该节点是唯一可以和 $ v $ 交换的节点）

情况2：如果 $ v\in V\setminus S $ ，候选算子为SWAP和ADD。先使用SWAP，因为SWAP不改变解的质量，ADD会使解的质量变差。如果二者都不能执行，算法就跳过节点 $ v $ 。

SWAP算子使用情形：（同时满足）

  • $ v $ 未在本 round 参与 SWAP 操作
  • $ v $ 的映射邻域 $ N^M(v) $ 非空。从 $ N^M(v) $ 中随机选择一个节点 $ u\in S $ ，然后移入 $ v $ ，移出 $ u $ 。

ADD算子使用情形：如果本次操作之后（ $ |S| + 1 $ ）仍然小于等于 $ Record + \delta $ （ $ Record $ 是最优解的顶点覆盖个数， $ \delta $ 是一个参数）

3.4 条件改进阶段

增强和多样化之间的平衡是SLS算法的另一个重要问题。阈值搜索过程提供了一种多样化的形式，因为它同时接受非改进和恶化的解决方案。为了补充这一点，需要一个强化程序，以确保更集中和定向的搜索。为此，在条件改善阶段采用爬山程序（算法1的第28-39行）。爬山过程的目的是使用从由阈值搜索阶段返回的解 $ 𝑆 $ 开始，使用DROP算子得到一个局部最优解。具体做法是迭代随机从 $ N_I(S) $ 中选择一个顶点，并将其从解决方案中剔除，直到 $ 𝑁_𝐼(𝑆) $ 变为空。爬山过程的局部最优是有趣的，因为它可以更新记录的最佳解 $ 𝑆^\ast $ （第33-34行，算法1）。

然而，从搜索过程的长期角度来看，通过这种技术确定的局部最优值不一定是下一轮阈值搜索阶段的良好起点。因此，条件改进阶段使用随机开关（“开”或“关”）来确定其输出解，该输出解将作为下一轮阈值搜索的起始解。本文提出的这一机制旨在平衡搜索的集约化和多样化。当开关处于“开启”状态时，输出解为局部最优解；否则，它是上一轮阈值搜索返回的解。该设计基于以下考虑。虽然阈值搜索程序提供了一种受控的多样化形式，使搜索能够摆脱一些局部优化，但由于 $ \delta $ 值所固定的质量限制，它可能不足以摆脱深层的局部优化陷阱。该算法并不试图逃脱这种陷阱，而是偶尔跳过它们。另一方面，由于一些局部最优很容易逃脱，而另一些最优则很难摆脱，所以从爬坡程序的局部最优开始下一轮阈值搜索也可能是有益的。

在我们的实现中，条件改进阶段首先设置 $ 𝑅𝑒𝑐𝑜𝑟𝑑 $ 值为当前最小顶点覆盖 $ S^\ast $ 的大小，并将阈值搜索阶段返回的解存储在 $ 𝑆^\prime $ 。然后执行爬山程序以获得局部最优值 $ 𝑆 $ ，并使用它更新记录的最佳解决方案 $ 𝑆^\ast $ 如果需要。如果随机开始是开”on”，就接受局部最优解 $ S $ ，并且设置 $ Record $ ，否则的话就继续使用 $ S^\prime $ 。