Benchmark-Problem Instances for Static Scheduling of Task Graphs with Communication Delays on Homogeneous Multiprocessor Systems
Abstract
在处理器上调度程序任务是高效使用多处理器系统的核心。大多数任务调度问题都是NP难问题,因此,除了最简单的情况外,启发式是所有情况下的首选方法。使用公认的基准问题实例集对于正确比较和分析启发式算法至关重要。然而,这类集合不适用于几类重要的调度问题,包括具有通信延迟的多处理器调度问题(MSPCD),其中人们感兴趣的是将依赖任务调度到同构多处理器系统上,处理器以任意方式连接,同时明确说明在分配给不同处理器的任务之间传输数据所需的时间。我们提出了MSPCD的测试问题实例,这些实例在处理器数量、多处理器体系结构类型、要调度的任务数量和任务图特征(任务执行时间、通信成本和任务之间的依赖密度)方面具有代表性。此外,我们以适当的方式定义任务图生成器,以确保相应的问题实例遵守文献中最近提出的理论原则。
关键词:多处理器系统,任务调度,通信延迟,基准问题实例
一、介绍
将程序模块(任务)调度到处理器是高效使用多处理器系统的核心,目前已有40多年的研究[14]。大多数任务调度问题都是NP难问题[12,27]。只有少数特殊情况可以在多项式时间内得到最优解[4,16,28]。对于所有其他问题变体,主要提出了启发式方法[11,18,22,24,25]。有关这些主题的最新调查,请参见[2,23]。
我们特别感兴趣的是将依赖任务调度到同构多处理器系统上的问题,其中处理器以任意方式连接,同时明确说明在分配给不同处理器的任务之间传输数据所需的时间。我们将这种任务调度问题称为带通信延迟的多处理机调度问题(MSPCD)。
通常很难分析和比较启发式算法的性能,即使它们处理相同的调度问题变量。一方面,很难获得理论上的绩效指标。另一方面,大多数论文都提出了新的测试实例,并且只报告了这些实例的性能结果,这一事实阻碍了实验分析。利用已确认的基准问题实例集(例如,或chttp://mscmga.ms.ic.ac.uk/info.html)报告计算结果有助于缓解这个问题。然而,这样的基准问题实例集并不适用于所有类别的调度问题。因此,很少有基准问题实例被提出用于多处理器系统上的任务调度[5,20,26]。此外,事实证明,这些问题通常针对特定的多处理器体系结构,不涉及通信延迟,对于问题的其他一些参数来说也不是很有挑战性。因此,需要一套更完整、更具挑战性的基准问题实例。
本文的目的是提出MSPCD的基准问题实例,这些实例在处理器数量、多处理器体系结构类型、待调度任务数量和任务图特征(任务执行时间、通信成本和任务之间的依赖密度)方面具有代表性。我们证明,我们提出的问题集克服了文献中其他测试问题集所显示的大多数缺点。此外,任务图生成器的定义使得相应的问题实例遵守Hall和Posner[13]最近提出的原则。
用于评估拟定测试问题实例的调度启发法,以及文献中存在的与MSPCD相关的调度启发法,提供了主要启发方法的合理表示:呼吸/深度优先搜索、通信的显式/隐式处理、基于优先级/依赖性的任务选择,使用处理器数量的最小化/最大化,等等。因此,我们不仅可以确认一个众所周知的事实,即每个启发式都有“简单”和“困难”图,而且最重要的是,可以解释调度结果如何依赖于任务图和多处理器系统的特征。
综上所述,本文的主要贡献有:
- 对与MSPCD相关的调度问题的现有测试问题集进行了批判性分析;
- MSPCD的新基准任务图集,这是文献中尚未直接考虑的一个问题变量,具有确保公平评估调度算法的参数变化;
- 对提出的基准问题实例集进行理论分析。
论文的结构如下。第2节描述了MSPCD调度问题,以及用于实验评估的调度启发式算法。第3节回顾了文献,分析了现有的测试问题实例集,指出了不足之处,并指出了对新问题集的需求。第4节将描述我们提出的基准问题实例,以及相应的任务图生成器。第5节对这些装置进行了实验分析。第6节总结全文。
二、MSPCD调度问题
在本节中,我们首先回顾MSPCD问题的基于图的组合公式。然后,我们描述了用于评估测试问题实例集的调度启发式算法的特征。
要调度的任务由一个由元组 $ G=(T,E,C,L) $ 定义的有向无环图(DAG)[6,17,25]表示,其中 $ T=\left\{t_{1}, \ldots, t_{n}\right\} $ 表示任务集; $ E=\left\{e_{i j} \mid t_{i}, t_{j} \in T\right\} $ 表示优先/通信边的集合; $ C=\left\{c_{i j} \mid e_{i j} \in E\right\} $ 表示边缘通信成本的集合; $ L=\{l_1,\dots,l_n\} $ 表示一组任务计算时间(执行时间,长度)。通讯成本 $ c_{ij} \in C $ 对应于在不同处理器上执行时在任务 $ t_i $ 和 $ t_j $ 之间传输的数据量。当两个任务都分配给同一个处理器时,通信成本等于零。集合 $ E $ 定义了任务之间的优先关系。一项任务只有在其所有前置任务都已完成执行且所有相关数据可用时才能执行。在本文考虑的问题版本中,不允许任务抢占和冗余执行。
其中 $ E $ 应该是一个拓扑图,输入数据
假设多处理器系统 $ M $ 包含 $ p $ 个相同的处理器,它们有自己的本地存储器。处理器通过同等容量的双向链路交换消息进行通信。该体系结构由距离矩阵建模[6,11]。距离矩阵D的元素 $ (k,l)=[d_{kl}]p×p $ 等于连接节点 $ p_k $ 和 $ p_l $ 的最小链接数。因此,距离矩阵是对称的,对角线元素为零。我们还假设构成多处理器系统的每个处理器都有用于所有通信链路的I/O处理单元,以便可以同时执行计算和通信。
DAG G到M的调度包括以最小化给定目标函数的方式确定G中每个任务的处理器索引和开始时刻。一个常用的目标函数(我们在本文中也使用)表示计划任务图的完成时间(也称为最大完工时间、响应时间或计划长度)。任务 $ t_i $ 的开始时间由其前置任务的完成时间以及将相关数据从执行这些前置任务的处理器传输到执行任务 $ t_i $ 的处理器所需的时间量确定。分别在处理器 $ p_k $ 和 $ p_l $ 上执行的任务 $ ti $ 和 $ tj $ 之间的通信时间可以计算为
其中, $ ccr $ 取决于体系结构,代表通信与计算比率,定义为一个数据单元的传输时间与执行单个计算操作所需时间之间的比率。(请注意,该定义是多处理器体系结构的特征;因此, $ ccr $ 不同于 Kwok 和 Ahmad[19,20]的 $ ccr $ 参数,后者定义为给定任务图的总通信和计算时间之间的比率,因此对应于任务图的特征。)当 $ l=k $ 时, $ d_{kl}=0 $ 意味着 $ \gamma_{i j}^{k l} $ 。
调度问题在大多数情况下都是NP难问题[12,27],除了最简单的情况外,通常使用启发式方法解决。对于一般的任务图调度问题[11,18,22,24,25],尤其是对于线性规划公式显示 $ n^6 $ 变量的MSPCD问题[10],情况也是如此。
针对任务调度问题提出的大多数启发式方法都基于某种优先级排序方案,包括两个阶段:任务排序和任务到处理器分配。然后,可以根据这两个阶段的顺序对启发式方法进行分类[15,23]。第一类启发式算法首先根据某种优先级方案对任务进行排序,然后是第二阶段,在第二阶段中,每个任务都分配给由某种调度规则选择的处理器。属于第二类的启发式算法首先将任务分配给处理器,而实际的调度,即任务之间的顺序和每个任务的开始时间的定义,则在第二阶段执行。对于表示的商品,我们将这两个类称为列表调度和聚类启发式。这两个类之间的区别在于,前者在分配任务之前根据指定的优先级对所有任务进行排序,而后者首先生成任务子集,然后分别对每个子集进行排序。
这两种算法都涉及任务排序和分配阶段的启发式规则。任务优先级可以根据任务执行时间、通信要求、后续任务的数量等来定义。可以合并并同时考虑多个标准。当考虑相互独立的任务时,启发式任务分配规则可以是breath first,也可以是depth first,在这种情况下,可以沿着任务图中的路径检查任务。调度问题和算法也可以根据与处理器数量相关的角色进行区分:可以使用所有可用的处理器,也可以尝试最小化使用的处理器数量。
我们选择了一组反映这些方法论方法的启发式方法,并使用它们来调查文献中提出的不同基准问题实例集以及我们自己的基准问题实例集的特征。四个列表调度和两个聚类启发代表了我们的选择。
第一个列表调度启发式表示为 CPES,是对动态级别调度(DLS)启发式的修改[25]。DLS的基本思想是基于关键路径(CP)方法计算静态任务优先级,并使用它们对任务进行排序,然后在调度阶段修改它们,以反映已生成的部分调度(选择最佳(任务、处理器)对进行调度)。优先级的动态更新在一定程度上改善了调度阶段的性能,但也显著增加了计算负担。因此,我们决定只使用基于 CP 的静态优先级。请注意,关键路径的计算不涉及通信时间,因为这些时间取决于最终任务到处理器的分配和调度。因此,只考虑任务执行时间 $ l_i $ 。最早开始(ES)启发式用于调度,这意味着计算每个任务 $ t_i $ 和处理器 $ p_k $ 的开始时间 $ st(t_i,p_k) $ ,任务分配给具有最小相关开始时间值的处理器[6]。
CPES 算法,列表调度
我们还实现了去聚类(DC)列表调度算法[6]。第一阶段基于基于CP的优先级列表,该列表定义了顺序执行顺序(即,当所有任务都分配给单个处理器时的任务顺序)。在第二阶段,只要任务能够改善当前的调度,任务就会一个接一个地转移到其他可用的处理器。对于密集任务图,这种方法被证明是非常有效的。对于密集任务图,由于进程间的数据交换,大多数启发式算法都会产生具有大量空闲时间间隔的解,从而导致并行执行时间比顺序执行时间长[6,15]。
DC 算法,列表调度
文献提示,当涉及通信时间时,CP规则可能无效[2,11,15]。因此,我们还实现了之前方法的两个变体,LPTES和LPTDC,它们利用最大处理时间(LPT)[3]规则来构建第一阶段的优先级列表。
LPTES算法:是 CPES 的变种,列表调度
LPTDC算法:是 DC 的变种,列表调度
首选路径选择(PPS)[21]和最小化通信负载平衡(LBMC)[24]是我们实现的两种聚类启发式算法。第二种方法的主要思想是在第一阶段对任务进行集群,从而平衡处理器负载,最小化处理器间的通信。PPS方法通过给定的DAG构建路径,这样,如果某个任务的至少一个前辈已经属于该路径,则该任务将包含在该路径中。对于一个任务,包含最多前辈的路径被标识为首选路径。然后使用首选路径确定簇。这两种方法都包括第二阶段来计算每个处理器上的实际调度。
PPS 算法、LBMC算法,聚类启发式
实际上是四种算法,CPES,DC,PPS,LBMC
让我们在这里总结一下所选调度算法之间的差异:CPES是贪婪的呼吸优先启发式算法,而PPS执行深度优先搜索{或链接[11]}。LBMC明确考虑了通信的最小化,而DC包括通信时间,以改进顺序调度。此外,虽然CPES和DC的目标是尽量减少处理器数量,但LBMC和PPS正在使用所有可用的处理器。因此,选定的程序涵盖了主要的调度启发式设计,并用于本文报告的所有实验。
三、现有的基准问题实例集
大多数描述调度问题的基准问题实例的论文考虑比MSPCD更简单的情况,例如没有通信成本的DAGS或完全连接的多处理器体系结构。因此,在文献中只能找到几组与MSPCD有关的测试问题实例。我们将在本节中回顾这些努力。我们的目标是使其适用于MSPCD的基准启发式。我们的评估基于实验结果以及霍尔和波斯纳[13]提出的标准。
Hall和Posner[13]讨论了生成代表性测试问题实例的问题,以分析和比较调度问题的启发式算法。他们指出,需要一组测试问题来解决给定的调度问题变量,但与问题特征无关,因此可以用于对相应算法的公平评估。霍尔和波斯纳定义了代表性的测试示例集应该满足的原则。他们通过描述两个调度问题的测试问题的生成过程来说明这些原则:随着发布日期最大拖期的最小化,以及随着截止日期加权完成时间的最小化。这些问题比MSPCD更复杂。因此,我们假设霍尔和波斯纳提出的原理和性质适用于这个更简单的情况。控制测试问题实例生成的原则是:
目的,生成的示例必须能够分析和比较给定调度问题的算法;
可比性,示例不应取决于实验环境的任何特征;
不带偏见,生成过程应避免包含任何问题特征;
再现性,生成过程应简单明了,以便易于重复生成新的充分数据。
生成过程应显示以下属性:
多样性,问题生成器必须创建范围广泛的问题实例;
相关性,即创建模拟真实世界情况的测试实例;
规模
规模不变性,以确保结果不会取决于问题实例的规模;
当以类似的方式处理相同类型的输入时,生成过程满足正则性;
可描述性
效率
简约性,以确保生成过程易于描述,易于实施、使用和复制,并且最终,只有可能影响分析的参数是不同的。
[13]解释了原理和性质之间的关系。在下文中,我们描述了关于它们的现有问题实例集。
Coll、Ribeiro和de Sousa[5]提出了一组规模相对较小且没有通信延迟的问题。此外,调度结果仅适用于完全连接的异构多处理器系统。因此,这些测试问题实例不适用于MSPCD。
Tobita和Kasahara[26]提出的大量问题实例也得出了类似的结论。问题实例生成器满足[13]的大多数原则和属性(简约标准似乎没有严格执行)。然而,没有考虑通信延迟和任意多处理器体系结构,这使得这些测试问题实例不适合MSPCD。(附录2给出了在某些问题实例上使用所选启发式的调度结果。)
根据作者的知识,Kwok和Ahmad[20]提出了与本文所述问题密切相关的唯一现有问题实例集。他们考虑了通信延迟。然而,多处理器体系结构被认为是完全连接的。
Kwok和Ahmad[20]收集了文献中提出的15种调度算法,并生成了几组测试实例来比较它们。作者将调度算法分为五组,并比较了组内的算法。这五组算法分为SRC(调度限制图)、TDB(基于任务重复的)、UNC(无界群集数)、BNP(有界(完全连接的)处理器数)和APN(任意处理器网络)。因此,APN是唯一一组似乎适合MSPCD的算法,但[20]中未对其进行详细分析。
测试实例也被划分为多个组。并非所有的调度算法都适用于所有组。提出的任务图组包括PSG(包含从文献中收集的小型图的对等集图)、RGBO(具有分支和定界获得的最优解的随机图)、RGPOS(具有预选最优解的随机图)、RGNOS(具有未知最优解的随机图),和TG(跟踪图,代表真实世界的应用程序)。PSG和TG包含特定结构的图形(例如三角形或菱形),它们的特征、调度环境和结果没有详细说明。因此,我们专注于剩下的三组RGBOs,RGPOS和RGNOS,考虑通信延迟,即使结果只报告完全连接的处理器网络。考虑任意处理器网络(APN)的调度算法集可以应用于这些实例。我们实现的所有调度算法都可以归类为APN,有些类似于[20]中使用的算法(例如DLS和DC)。
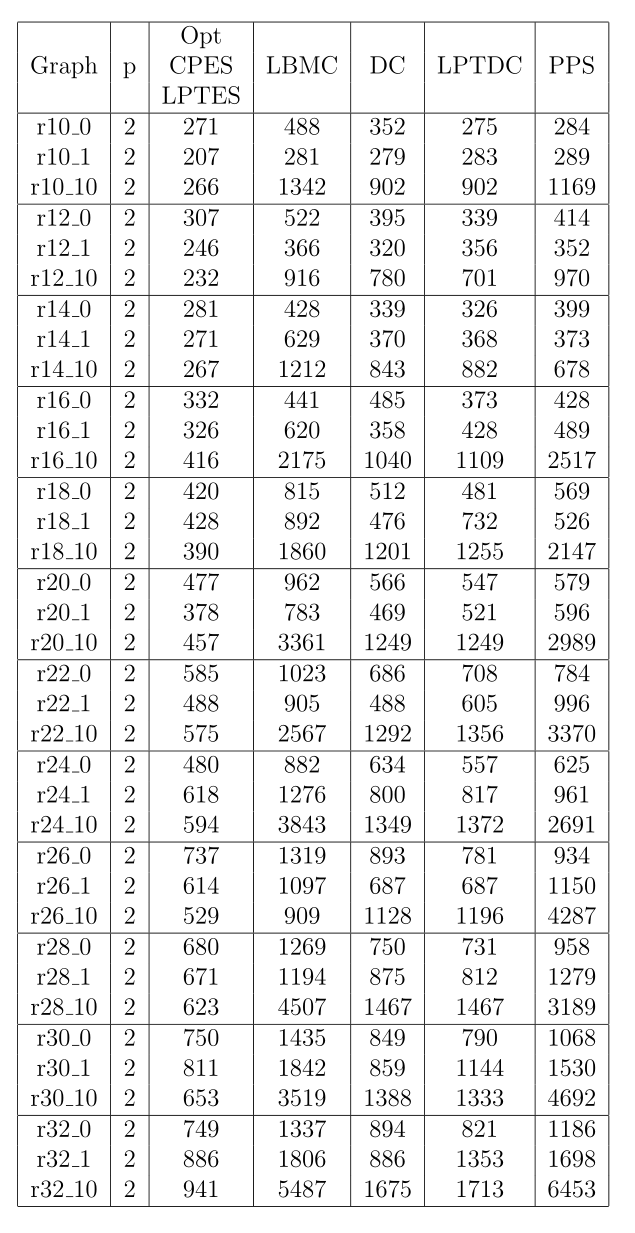
RGBOS测试示例集包含36个图,其中3个图的CCR参数(0、1和10)的值不同,分别对应于12个DAG大小中的每一个,任务数n从10到32,增量为2。这些小例子的最优解是通过使用 $ A\star $ 枚举算法[1]算出来的。[20]中报告的在两处理器系统上调度这些任务图的启发式结果显示,与最佳值的偏差为1%到8%。表1给出了使用我们选择的启发式方法获得的结果。CPES和LPTES总是产生最佳解决方案。
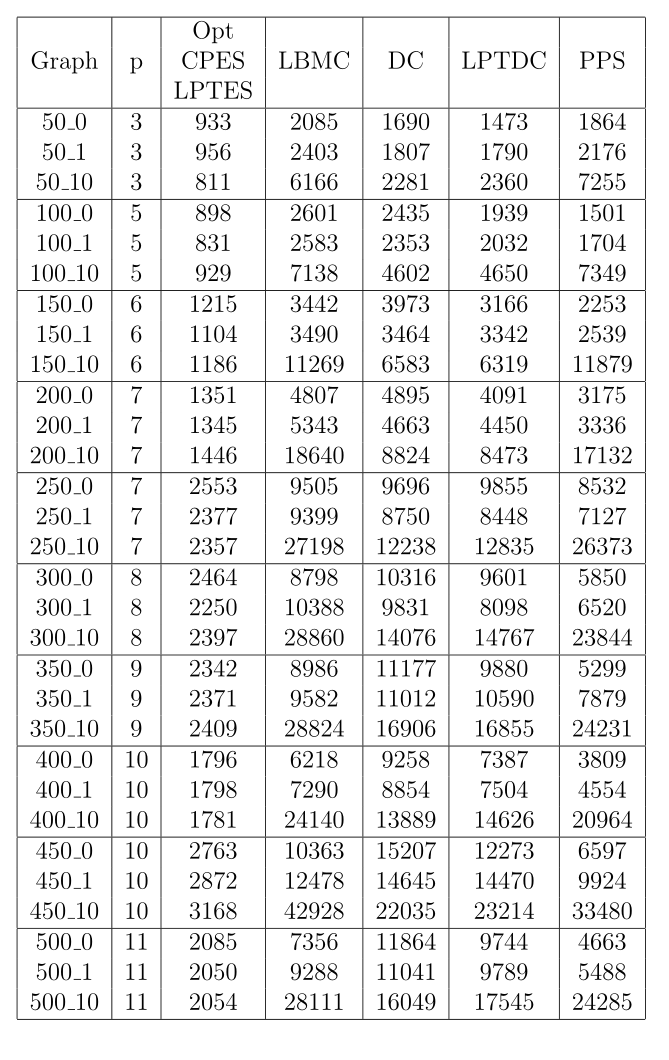
第二组测试问题实例RGPOS由30个实例组成,这些实例具有针对完全连接的多处理器系统的预选最佳解决方案。对于这些示例,n的范围从50到500,增量为50,对于每个n,CCR参数使用相同的三个值。报告了11种调度算法的调度结果,平均偏差为2%至15%。仅在少数情况下获得了最优解。令人惊讶的是,在[20]研究中,来自APN组的大多数调度算法没有应用于来自RGBO和RGPOS集的测试实例。这些集合不能代表任意多处理器体系结构的事实并不排除APN算法的使用。我们对RGPOS问题实例的实验结果如表2所示。令人惊讶的是,如前所述,CPES和LPTES启发式算法为所有问题实例提供了最优解决方案。
CPES和LPTES启发式算法的性能不能用它们的设计或内在品质来解释。例如,我们的经验表明,CPES获得的结果可能偏离最佳值 $ 100\% $ 以上[8,9]。因此,我们分析了这两组任务图(RGPOS,RGBOS),发现它们都显示出非常相似的边缘(连接)密度。图的边密度 $ \rho $ 定义为边数除以完全图的边数(即 $ \rho = \frac{|E|}{n(n - 1) / 2} $ ). 对于 RGBOS, $ \rho $ 在 $ 30\% $ 到 $ 40\% $ 之间变化,而对于RGPOS中的图形, $ \rho $ 的值在 $ 4\% $ 到 $ 10\% $ 之间。 总之,这两个集合只包含稀疏任务图,而RGPOS图包含几乎独立的任务。
因为 RGPOS 中密度太低了
进一步的分析表明,事实上,这两组问题实例违反了Hall和Posner[13]所要求的几个属性。因此,由于图形密度不变,且未考虑多处理器体系结构中的差异,因此无法确保多样性。实际上,对于每个尺寸 $ n $ ,只考虑一个具有固定数量完全连接处理器的多处理器系统。由于只考虑完全连接的多处理器系统,因此也不提供相关性。由于任务图和最优解的结构是预先确定的,因此RGPOS 示例也违反了规则性。因此,可以很容易地定义始终会生成最佳计划的计划程序。因此,在[20]中提出的 RGBOS 和 RGPOS 问题实例集不足以对MSPCD问题的算法进行基准测试。
关于这两个集合上的其他启发式行为的注释。从表1和表2可以看出,LBMC和PPS表现最差。LBMC的主要问题是,在集群期间,通过将任务分配给集群而产生的通信延迟的近似性较差。简单的试探法,例如考虑最大任务间通信延迟[24]或通信延迟的加权和,似乎不起作用。至于PPS启发式算法,它最初是为细粒度任务执行时间和通信延迟而设计的,但这里的情况并非如此。
[20]中提出的第三组问题实例可用于为一般网络设计的启发式算法,是由250个随机任务图组成的集合RGNOS,生成的任务图与RGBOS中的类似,但任务数与RGPOS集合的任务数范围相同。作者提供的关于这个集合和APN算法的信息很少。既没有提供最佳解决方案,也没有提供最知名的解决方案,也没有指定处理器的数量。因此很难进行比较。然而,我们将选定的启发式方法应用于50个任务的子集,其中 $ CCR=1.0 $ , $ p=2 $ 。启发式的相对行为与之前观察到的类似。如附录2所示,可获得完整的结果。值得注意的是,RGNOS中任务图的密度也非常低,从8%到15%不等。至于[13]所要求的属性,RGNOS并不违反相关性和规律性,但由于只生成了稀疏图,所以仍然不能满足多样性。
RGNOS 的缺点
四、新的基准问题实例集
我们提出了两组新的任务图,用于分析和比较解决MSPCD问题的调度启发式算法。第一个由随机生成的DAG组成。生成程序和参数设置(例如,边缘密度)可以执行[13]中的规则和原则。第二组包含任务图,其中包含给定多处理器体系结构的已知最佳解决方案。在本节中,我们将描述这两个集合的问题实例和相应的任务图生成器。如附录1所示,可从作者处获得任务图。
两个新的集合,包括相应的个生成器
为第一组问题实例构建了两个生成器。第一个生成具有给定高度和宽度的任务图(即,具有预选数量的“层”和层内的任务;但是,应该注意的是,我们不强制多层设计)。这样的任务图显示了预定的并行水平,因此适合于涉及不同多处理器系统架构的实验。生成器还允许控制影响任务图其他特征的输入参数,如粒度、CCR因子([20])和密度。
第一个样例集有两个生成器,第一个生成器生成 高度、宽度
第二个生成器生成具有预选密度的任务图。这样就克服了[20]中提出的集合的主要缺点。任务执行时间和通信延迟根据给定的输入参数随机确定。可以为相同的输入参数值生成多个图形。然而,这个过程的随机性确保了结果图是不同的。
第一个样例集的第二个生成器,生成具有预选密度的图
两个生成器的几个输入参数相同:要生成的图的数量、每个任务图中的任务数量、任务持续时间(执行时间)的最大值以及通信延迟的最大值。对于第一个生成器,每个图中的最大级别数(高度)和每个任务的最大后续数都是特定的,而生成的任务图的密度仅出现在第二个生成器中。这些参数的实际值是在生成过程中为生成的每个特定任务图随机确定的。由于在生成过程中没有对问题特定参数进行任何假设,因此这些生成器遵循[13]中提出的原则。
第一个样例集的参数
这两个生成器用于构建第一组测试示例。它由180个随机任务图和 $ n \in \{50,100,200,300,400,500\} $ 和 $ \rho \in \{20, 40, 50, 60, 80\} $ . 对于每个 $ (n,ρ) $ 组合,我们生成了 $ 6 $ 个图,其中包含控制任务计算时间和通信需求的不同参数组合。第一个生成器生成了三个大小相同的任务图,第二个生成器生成了另外三个任务图。因此,对于每个 $ n $ ,有 $ 30 $ 个具有相同任务数的任务图(每个 $ n $ 有五组,每组六个图),而对于每个 $ \rho $ ,有36个具有相同密度的图(每个 $ \rho $ 有六组,每组有六个图)。所提出的任务图不依赖于多处理器体系结构。它们可以调度到任意多处理器系统。
第一个样例集组成,180个图,图的构成
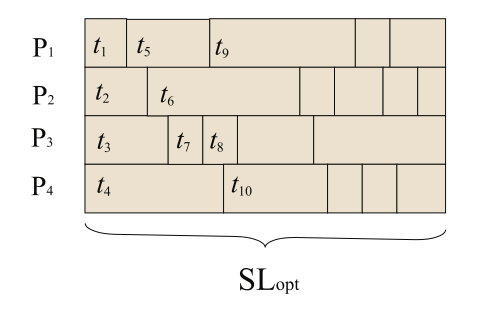
我们还提出了一组新的随机生成的测试实例,它们具有已知的最优解,克服了[20]的一些局限性。生成过程如下。对于多处理器体系结构的每种组合,都会生成许多图 $ m $ (此处设置为10),这些图由处理器数量 $ p $ 和距离矩阵 $ D_{p\times p} $ 、任务数量 $ n $ 和以及最优调度 $ SL_{opt} $ 的长度 。所有 $ m $ 图都包含相同数量的任务,任务持续时间相同,但边密度 $ \rho $ 不同。首先,生成最佳调度的方式是,每个处理器 $ p_k $ 执行的任务数量 $ x_k $ 大致相同(允许偏差为 $ 10\% $ )。任务持续时间采用均匀分布随机确定(平均值等于 $ SL_{opt}/x_k $ 和 $ 10\% $ 偏差)。所有处理器都在同一时间完成执行(SLopt),任务之间没有空闲时间间隔。然后根据任务的开始时间对任务进行编号:第一个处理器上的第一个任务获得数字 $ 1 $ ,第二个处理器上的第一个任务获得数字 $ 2 $ ,依此类推; $ p+1 $ 将是第二个任务的开始时间最小的数量(无论对应处理器的索引如何); $ p+2 $ 将与下一个开始执行的任务相关联(如果前一个任务的持续时间很短,则该任务可能位于同一个处理器上);图1说明了通过该程序获得的最佳进度的结构。
m 代表图的编号
任务之间的优先关系是通过向图中添加边并为这些边分配通信负载来定义的。首先计算最大允许密度 $ \rho_{max} $ ,因为如果 $ st(t_i,p_k)+l_i > st(t_j,p_l) $ ,任务 $ t_i $ 到 $ t_j $ 之间不可能有边。然后,对于每个 $ i=0,\cdots,m−1 $ ,计算与密度 $ \rho_{max}·i/m $ 对应的边数,并将新边随机添加到任务图中以达到该数。沿每条边的通信要求(边权重)按以下规则计算:
即,例如,当任务在同一处理器上执行时,交换的数据量可以是任意大的,否则,通信量由第一个任务的完成时间和第二个任务的开始时间之间的间隔除以相应处理器之间的距离来定义。生成的任务图成为构建密度更高的实例的起点(只需添加几个新边)。
因此,该生成器的输入参数是:要生成的任务图的数量、每个任务图中的任务数量、处理器的数量、相应的距离矩阵以及最佳调度的长度。然后,如前所述,计算每个处理器的任务数、任务持续时间和通信请求。
第二个样例集的参数
该集合由 $ 700 $ 个问题实例组成,这些实例在多处理器系统架构(处理器数量和距离矩阵)、任务数量和任务图密度方面具有不同的特征。我们选择了 $ 7 $ 种不同的多处理器系统配置,这些配置由连接体系结构和处理器数量 $ p $ 定义:维度为1、2、3和4的四个超立方体(即2、4、8和16个处理器),以及6、9和12个处理器的三种网格配置。通过组合相应任务图的任务数n(10个值从50增加到500,增量为50)和连接密度 $ \rho $ (10个值从0(独立任务)到最大允许密度 $ \rho_{max} $ 的90%),为7个系统配置中的每一个生成了100个问题实例。这些测试实例不满足[13]中提出的所有属性:第二个和第三个属性不满足,因为预先指定了多处理器体系结构和最终(最优)调度的结构。然而,对于估计给定启发式算法提供的解决方案质量,问题实例集可能仍然非常有用。
表3给出了DAG中每 $ n $ 个任务的最佳计划长度。这些长度不取决于 $ p $ 和 $ \rho $ 的值。所提出的问题实例集还可用于在完全连接的体系结构上进行调度,以及在与通信延迟无关的情况下进行调度。

五、新问题集的调度结果分析
在本节中,我们报告并分析将选定的启发式应用于前一节中介绍的两组任务图的结果。启发式解决方案的质量与任务图特征和多处理器体系结构有关:任务数 $ n $ 、边缘密度 $ \rho $ 、处理器数 $ p $ 、互连体系结构和通信延迟。值得强调的是,我们的目标不是比较调度启发法,而是说明所提出的问题实例集作为基准的价值。因此,我们强调测试示例在参数变化和算法行为方面的特征。
超立方体是一种广泛使用的多处理器体系结构。因此,我们对1维、2维和3维超立方体进行了实验,也就是说,我们设置 $ p=2,4,8 $ 。三维超立方体的距离矩阵为

对于 $ p=2 $ 和 $ p=4 $ ,各自的距离矩阵由矩阵 $ D $ 的相应左上角块表示。为了表明即使在极端情况下也可以使用建议的问题实例,我们还考虑了通信延迟可以忽略不计的完全连接的体系结构和系统。
我们首先展示了第一组问题实例(集合1)的结果,其中包含没有已知最优解的随机任务图。完整的结果集太大,无法包含在论文中。仅给出平均结果。如附录2所示,可从作者处获得整套结果。
表4显示了在具有显著通信延迟的1维、2维和3维超立方体网络上调度的比较结果。第一列显示任务数,第二列显示处理器数。下一栏(一大栏)显示了30个大小相同的测试实例的平均值:第三栏显示了最为人所知的平均结果(调度长度),而其余六栏包含与第三栏中报告的最佳调度的平均偏差百分比。在大多数情况下,最佳解决方案由CPES获得。在其他启发式方法中,LPTES、DC和LPTDC在少数情况下产生了比CPES更好的解决方案,尽管它们的平均性能并不好。在下文中,我们将重点说明拟议问题实例特征的变化(由于生成过程中的参数变化)如何导致算法行为的适当变化,从而显示拟议问题集对MSPCD问题启发式评估的兴趣。
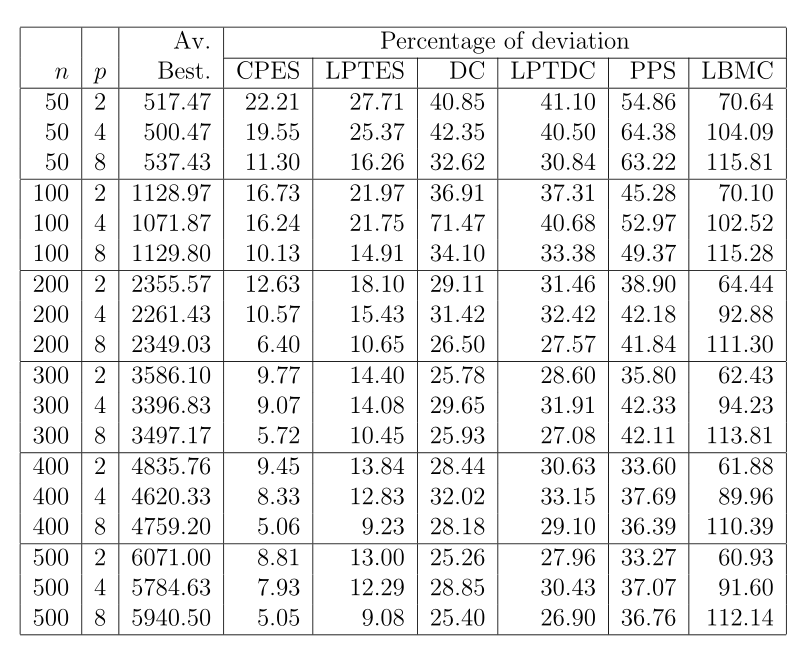
表4中的图说明了调度结果对处理器数量的依赖性。正如预期的那样,对于呼吸优先启发式算法,如CPES和LPTES,它们试图最小化使用的处理器数量,当处理器数量增加时,偏差会减小。对于其他启发式算法,可以观察到相反的趋势,这可以通过对应于更多处理器的额外通信负担来解释。图2说明了在 $ n=200 $ 和各种图形密度下,启发式算法在偏离最佳调度长度方面的性能。对于n的其他值,也可以观察到相同的行为。为了更清晰地表示,不包括基于LPT的启发式,因为LPTES和LPTDC分别显示与CPES和DC相似的行为。图2中显示的结果表明,所有启发式算法的性能都随着任务图的密度而增加(即,与最为人熟知的解决方案的偏差减小)。这意味着稀疏任务图通常更难通过调度启发式来处理,而对于更密集的图则更容易处理。这些结果还说明了前面提到的处理器数量与每个启发式算法获得的解的质量之间的关系:CPES的性能随着处理器数量的增加而提高,而其他启发式算法的性能则降低。
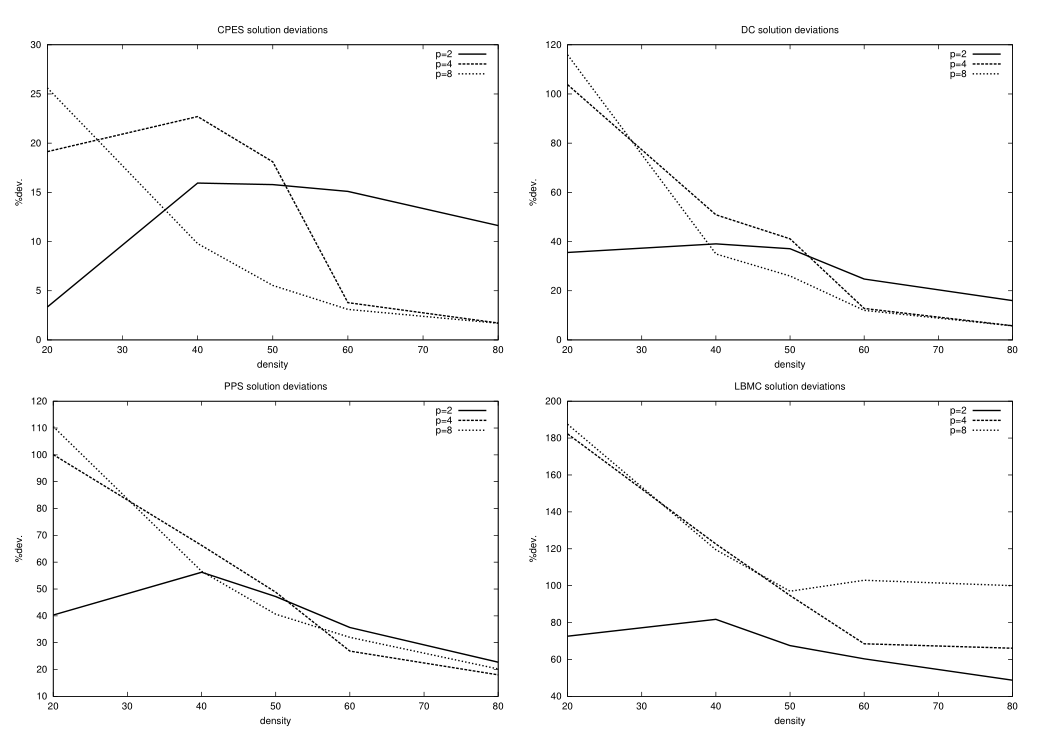

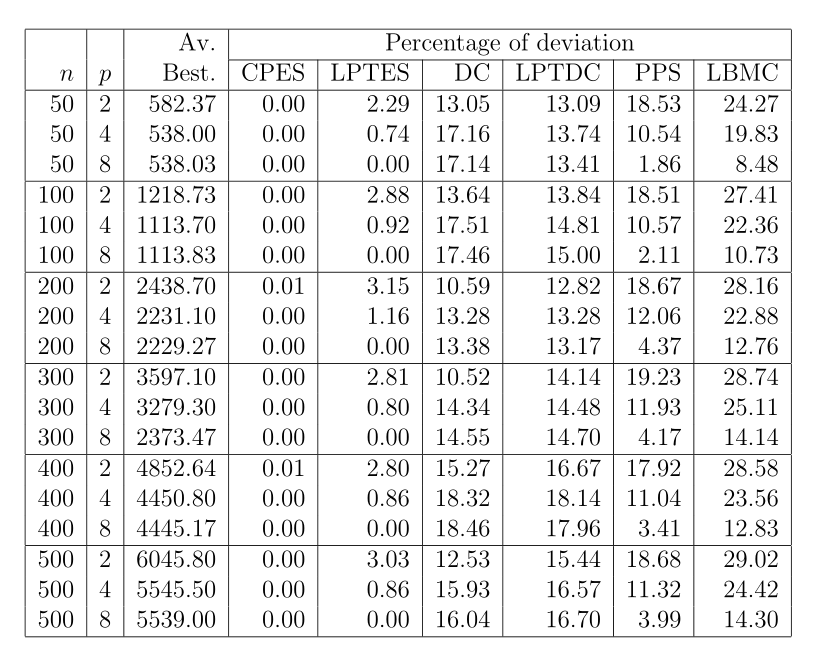
表5和表6分别显示了完全连接的处理器网络(对于 $ p=2 $ ,超级立方体和处理器的完全互连网络是同一个系统)和无通信延迟的DAG的调度结果。以前的大多数结论也适用于这些极端情况。然而,值得注意的是,PPS和LBMC启发式算法相对于处理器数量表现出不同的行为:当处理器数量减少时,解决方案的质量会下降。然而,它们的总体表现很差,这一观察结果不能被认为是确定的。需要改进这些启发式方法,但这超出了本文的范围。
一个重要的观察结果是,平均而言,当添加更多处理器时,最佳解决方案(第3列)不会得到改善。对详细结果的分析表明,稀疏任务图得到了一些改进,而密集任务图的解质量有所下降。密集图似乎不能从将处理器添加到多处理器系统中获益,因为等待前置任务完成其执行以及在不同处理器上调度的相关任务之间传输数据所花费的时间。此外,基于ES的启发式算法通常表现最好,但并不打算使用所有处理器。因此,在大多数情况下,即使可用处理器的数量增加,它们也会生成完全相同的时间表。同样的结论适用于没有通信延迟的问题实例。
已知最优解(集合2)的 $ 700 $ 个随机测试实例的详细结果见[7]。在本节中,我们总结了这些结果,并使用CPES启发式给出了数量有限的示例。
首先分析边缘(通讯)密度对溶液质量的影响。由于每个 $ p $ 的结果相似,我们在图3和图4中仅显示了 $ p=8 $ 的结果。每个图形显示 $ 10 $ 条曲线,每 $ n $ 一条,显示当 $ \rho $ 增加时偏离最佳解的变化。考虑了两种处理器数目固定的多处理器体系结构:根据给定的互连结构(网状或超立方体)连接的多处理器体系结构和完全连接的多处理器体系结构。我们还区分了有无通信延迟的情况。在后一种情况下,互联网络不起任何作用。因此,每个 $ p $ 仅存在三种情况(并显示三个图表):具有和不具有通信延迟的特定互连网络(图3),以及具有通信延迟的完整互连网络(图4)。例外情况是 $ p=2 $ ,因为特定连接和完整连接是相同的,只需分析两种情况。
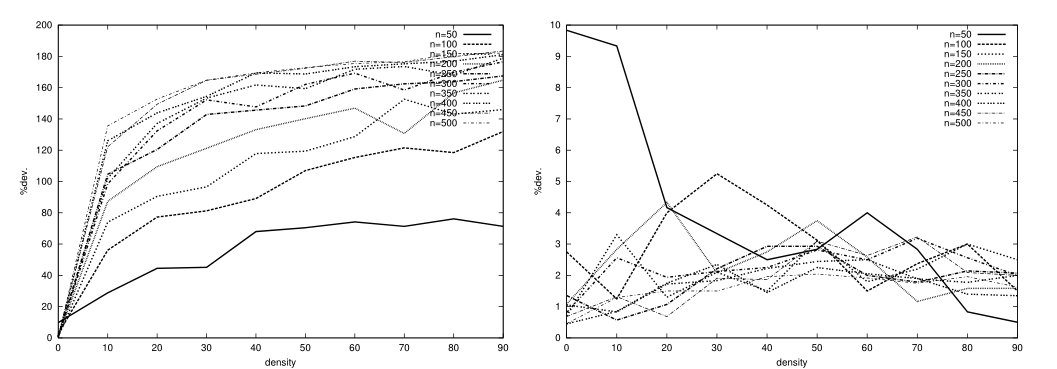
如图3和图4所示,当通信时间显著时,与最优解的偏差通常随 $ \rho $ 的增大而增大。这强调了一个事实,即集合2的问题实例,由于其用于提供已知最优解的特殊结构,其行为与集合1的完全随机测试问题截然不同。这些图还说明了处理器连接类型对这些问题实例的调度启发式解决方案质量的影响。对于完全连接的系统,增加 $ \rho $ 的影响似乎相对较小,而增加 $ n $ 的影响似乎可以忽略不计。然而,对于大量处理器来说,性能似乎有所下降。对于没有通信时间的系统,偏差在所有情况下都非常小。对于不完全连接的系统,观察结果是完全不同的:与最佳值的偏差可能非常大,比完全连接的系统大一个数量级。此外,偏差似乎随着 $ n $ 的增加而增加。最后,结果表明,集合2中的稀疏任务图很容易使用CPES进行调度,这表明了[20]中问题实例的缺点,这些问题实例都是使用这种启发式优化调度的。
第二个主要分析涉及处理器数量对调度结果的影响。在处理器数量较少的系统上调度比在较大的多处理器系统上调度更容易,这是很自然的。数据依赖性确实可以防止对大量可用处理器的有效利用。有时,处理器的数量甚至可能太多,导致在数据传输上花费的时间非常长,正如我们在调度集合1中的示例时已经注意到的那样。
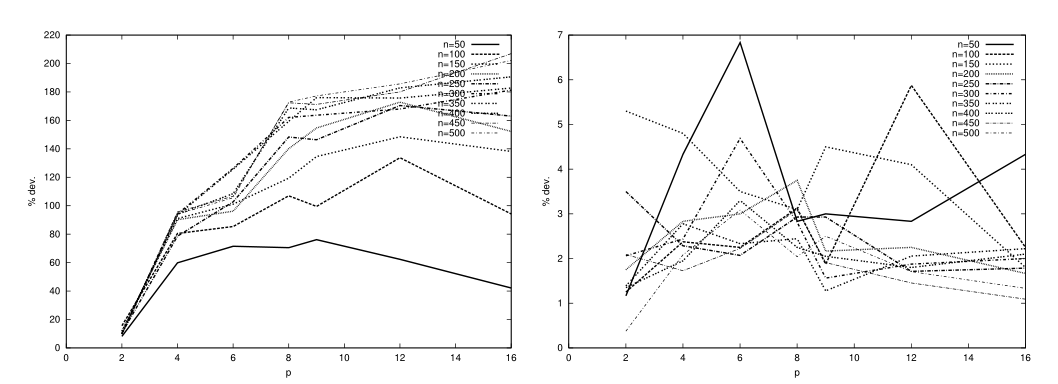
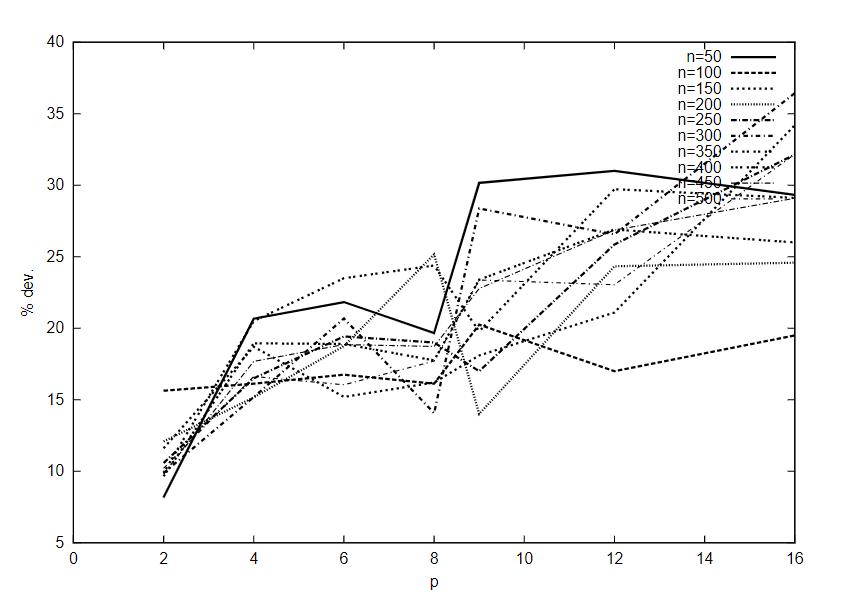
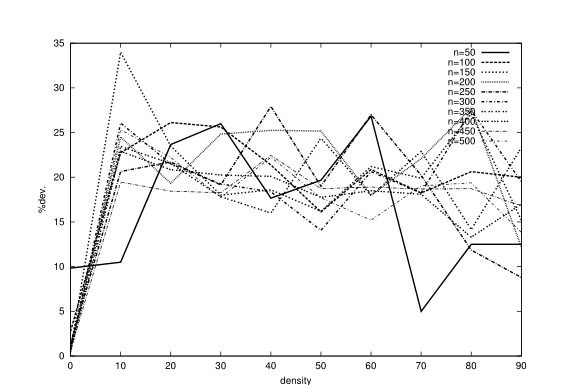
图5和图6显示了CPES在固定密度( $ \rho=50\% $ )下,针对不同数量的处理器和任务图获得的进度长度偏差。结果支持了前面的假设:当通信时间显著时,与最优解的偏差随着处理器数量的增加而增加。有趣的是,当可以忽略通信时,曲线非常接近(最大偏差为 $ 7\% $ ),且偏差不随 $ n $ 增加。对于完全连接的系统,也可以观察到这种趋势,但其较弱(偏差以较慢的速度增加)。另一方面,当通信时间不相关时,可以获得更好的任务分配。这些观察结果为CPES的性能提供了第二种解释,CPES为所有问题实例找到了最佳的时间表,从[20]:为每个大小 $ n $ 给出的 $ p $ 的单一值足够低,使问题“容易”。
因此,与密集的任务图相比,使用CPES调度稀疏的任务图似乎更容易。此外,当处理器数量相对较少时,可能会获得更好的结果。我们相信,对于所有的调度启发法来说,都存在这样的困难或简单的问题实例,并且我们提出的问题实例集足够大,可以在大多数情况下包含具有挑战性的问题。我们谨慎地改变与任务图和多处理器系统的特征相关的参数,以及LBMC、PPS和DC启发式对同一组任务图的结果(完整结果见[7]),支持了这一主张。结果表明,PPS和DC在调度密集任务图时遇到了与CPES相同的困难。此外,DC方法不区分不同类型的处理器连接。正如预期的那样,考虑到其通信最小化启发式规则,LBMC似乎很难处理稀疏任务图(独立任务除外,其行为类似于LPT方法)。当任务图的密度增加时,我们注意到解的偏差减少。对于所有启发式算法,偏差都会随着处理器数量的增加而增加,除了LBMC和PPS,它们似乎在通信重要时比12处理器网格更容易处理四维超立方体(p=16)。
已知最优解的完整测试实例集相当大,可能不需要在所有情况下使用所有示例。然而,根据我们的分析,两个参数 $ p $ 和 $ \rho $ 中至少有一个应该改变。这可以将集合的大小减少一个数量级(需要评估70或100个示例,取决于参数 $ p $ 或 $ \rho $ 的变化)。基于六种构造性启发法的实验,我们得出结论, $ p $ 和 $ \rho $ 是等价的,因为它们的变化为用户提供了洞察力。由用户决定更改哪一个。我们相信这个结论也适用于其他方法。
六、结论
在本文中,我们提出了两组新的基准问题实例,用于将依赖任务调度到不同的多处理器体系结构上,考虑到通信延迟(MSPCD),这些结构不一定完全连接。第一组包含完全随机的实例,可用于任何多处理器体系结构。这在理论上是合理的和普遍的。第二组包括针对特定处理器互连网络的已知最优解决方案的问题实例。此外,还对发电机进行了说明,并使其可用。
在本文中,我们提出了两组新的基准问题实例,用于将依赖任务调度到不同的多处理器体系结构上,考虑到通信延迟(MSPCD),这些结构不一定完全连接。第一组包含完全随机的实例,可用于任何多处理器体系结构。这在理论上是合理的和普遍的。第二组包括针对特定处理器互连网络的已知最优解决方案的问题实例。此外,还对生成器进行了说明,并使其可用。
使用了几种有代表性的启发式方法来评估文献中的问题集实例以及我们提出的问题集实例。我们分析了启发式解与已知解或最优解之间的偏差对几个参数的依赖性:任务图密度、通信延迟、处理器数量以及它们之间的连接。这些参数对启发式解决方案的质量起着重要作用,在测试调度启发式时,应改变这些参数,以确保公平评估。我们注意到,通信延迟显著降低了调度启发式算法的性能。关于多处理器体系结构,当然更容易调度到完全连接的处理器上,但这并不总是可能的。因此,处理器互连的类型也应该有所不同。对于另外两个参数,处理器数量和任务图密度,至少其中一个参数应该是不同的,以便客观地评估特定调度启发式的效率。我们提出的问题实例集提供了这种变化。
MSPCD是一门难而重要的问题课。我们提出的测试问题实例弥补了文献中的一个空白,为MSPCD启发式的公平评估提供了一个理论上合理、实验上全面的框架。
致谢
这项工作得到了塞尔维亚国家科学基金会“数学优化模型和方法及其应用”项目1583号赠款的部分支持。加拿大自然科学与工程委员会(Natural Sciences and Engineering Council of Canada)通过其研究资助项目,以及魁北克省基金会(Fonds F.C.A.R.)也为这项工作提供了资金。
参考文献
[1] I. Ahmad and Y.-K. Kwok. Optimal and near-optimal allocation of precedence-
constrained tasks to parallel processors: Defying the high complexity using effective
search technique. In Proceedings 1998 International Conference on Parallel Process-
ing, pages 424–431, 1998.
[2] J. Blazewicz, M. Drozdowski, and K. Ecker. Management of resources in parallel
systems. In J. Blazewicz, K. Ecker, B. Plateau, D. Trystran, eds., Handbook on
Parallel and Distributed Processing, pages 263–341. Springer, 2000.
[3] B. Chen. A note on lpt scheduling. Operations Research Letters 14:139–142, 1993.
[4] Jr. E. G. Coffman and R. L. Graham. Optimal scheduling for two processor systems.
Acta Informatica 1:200–213, 1972.
[5] P. E. Coll, C. C. Ribeiro, C. C. de Sousa. Test instances for schedul-
ing unrelated processors under precedence constraints. http://www-di.inf.puc-rio.br/celso/grupo/readme.ps, 2002.
[6] T. Davidovi´c. Exaustive list-scheduling heuristic for dense task graphs. YUJOR
10(1):123–136, 2000.
[7] T. Davidovi´c and T. G. Crainic. New benchmarks for static task scheduling on
homogeneous multiprocessor systems with communication delays. Publication CRT-
2003-04, Centre de Recherche sur les Transports, Université de Montréal, 2003.
[8] T. Davidovi´c, P. Hansen, and N. Mladenovi´c. Scheduling by VNS: Experimental
analysis. In Proceedings Yugoslav Symposium on Operations Research, SYM-OP-IS
2001, S. Mini´c, S. Borovi´c, N. Petrovi´c, eds., pages 319–322, Beograd, 2001.
[9] T. Davidovi´c, P. Hansen, and N. Mladenovi´c. Variable neighborhood search for
multiprocessor scheduling problem with communication delays. In Proc. MIC’2001,
4th Metaheuristic International Conference, J. P. de Sousa, ed., pages 737–741,
Porto, Portugal, 2001.
[10] T. Davidovi´c, N. Maculan, and N. Mladenovi´c. Mathematical programming for-
mulation for the multiprocessor scheduling problem with communication delays. In
Proc. Yugoslav Symposium on Operations Research, N. Mladenovi´c, Dj. Dugoˇsija,
eds., pages 331–334, Herceg–Novi, 2003.
[11] G. Djordjevi´c and M. Toˇsi´c. A compile-time scheduling heuristic for multiprocessor
architectures. The Computer Journal 39(8):663–674, 1996.
[12] M. R. Garey and D. S. Johnson. Computers and Intractability: A Guide to the
Theory of NP-Completness. W. H. Freeman and Company, 1979.
[13] N. G. Hall and M. E. Posner. Generating experimental data for computational
testing with machine scheduling applications. Operations Research 49:854–865, 2001.
[14] T. C. Hu. Parallel sequencing and assembly line problems. Operations Research
9(6):841–848, 1961.
[15] A. A. Khan, C. L. McCreary, and M. S. Jones. A comparison of multiprocessor
scheduling heuristics. In H. J. Siegel, editor, Proceedings of the 8th International
Symposium on Parallel Processing, pages 243–250, Cancún, Mexico, IEEE Computer
Society, 1994.
[16] V. Krishnamoorthy and K. Efe. Task scheduling with and without communication
delays: A unified approach. European Journal of Operational Research 89:366–379,
1996.
[17] Y.-K. Kwok and I. Ahmad. Bubble scheduling: A quasi dynamic algorithm for static
allocation of tasks to parallel architectures. In Proceedings 7th IEEE Symposium of
Parallel and Distributed Processing (SPDP’95), pages 36–43, Dallas, Texas, USA,
1995.
[18] Y.-K. Kwok and I. Ahmad. Dynamic critical path scheduling: An effective technique
for allocating task graphs to multiprocessors. IEEE Transactions on Parallel and
Distributed Systems 7(5):506–521, 1996.
[19] Y.-K. Kwok and I. Ahmad. Efficient scheduling of arbitrary task graphs to multi-
processors using a parallel genetic algorithm. J. Parallel and Distributed Computing
47:58–77, 1997.
[20] Y.-K. Kwok and I. Ahmad. Benchmarking and comparison of the task graph schedul-
ing algorithms. J. Parallel and Distributed Computing 59(3):381–422, 1999.
23
[21] B. A. Malloy, E. L. Lloyd, and M. L. Soffa. Scheduling DAG’s for asynchronous mul-
tiprocessor execution. IEEE Transactions Parallel and Distributed Systems 5(5):498–
508, 1994.
[22] S. Manoharan and P. Thanisch. Assigning dependency graphs onto processor net-
works. Parallel Computing 17:63–73, 1991.
[23] M. Pinedo. Scheduling Theory, Algorithms and Systems. 2dn edition, Prentice Hall,
2002.
[24] A. K. Sarje and G. Sagar. Heuristic model for task allocation in distributed computer
systems. IEE Proceedings-E 138(5):313–318, 1991.
[25] G. C. Sih and E. A. Lee. A compile-time scheduling heuristic for interconnection-
constrained heterogeneous processor architectures. IEEE Transactions on Parallel
and Distributed Systems 4(2):175–187, 1993.
[26] T. Tobita and H. Kasahara. A standard task graph set for fair evaluation of multi-
processor scheduling algorithms. Journal of Scheduling 5(5):379–394, 2002.
[27] J. D. Ullman. NP-complete scheduling problems. J. Comput. Syst. Sci. 10(3):384–
393, 1975.
[28] T. A. Varvarigou, V. P. Roychowdhury, T. Kailath, and E. Lawler. Scheduling in
and out forests in the presence of communication delays. IEEE Transactions Parallel
and Distributed Systems 7(10):1065–1074, 1996.
附录1-任务图文件说明
zip压缩包文件 Bench.zip,可从以下网址下载http://www.mi.sanu.ac.yu/~tanjad/,包含180个完全随机的任务图和readme.txt。文件名是`t,其中应替换为相应图中的任务数,应替换为边密度,而是具有相同n和r值的图的索引(每个(n,r)`对有 $ 6 $ 个图)。在每个文件中,数据都以以下格式写入:
- 第一行包含任务数n;
- 接下来的 $ n $ 行包含任务 $ i=1, \cdots, n $ 的数据:索引 $ i $ ,任务持续时间 $ t_i $ ,继任者的数量 $ n_{succ} $ ,继任者元组 $ (s_j, c_{ij}) $ 代表第 $ j $ 个继任者和对应的通信总量
我们在文件 NonoptBestResults.dat 中记录了最著名的解决方案。(通过应用GA和VNS元启发式获得)。下表给出了该文件的结构,其中D=C表示完整的互连处理器网络,而D=H表示超立方体多处理器体系结构。每个n给出30个测试示例。
压缩文件Bench_opt.zip也可以在同一个网址上找到,它包含了已知最优解的任务图实例和相应的readme.txt文件。文件名是ogra<n> <r> <p>.td,其中n和r的含义与前面的情况相同,而<p>应该用给出最优解的处理器数量来代替。
附录2-完整的进度安排结果
表1和表2给出了在[20]中提出的RGBOS和RGPOS集的完整结果。由Kwok和Ahmad[20]提出的第三个集合包含250个任务图。由于作者没有提供任何调度结果,我们在一个子集上运行我们选择的6种调度算法并提供相应的调度结果。所选的子集包含50个任务图,具有不同的任务数和并行度,参数CCR=1.0的值相同。结果报告在RGNOS.RES文件中,该文件可以从以下网址下载:http://www.mi.sanu.ac.yu/~tanjad/。该文件采用类似LATEX的表格格式。任务的数量出现在第一列,计划长度出现在第三列。结果是根据调度启发式排序的,其缩写在单独的一行中,表示相应数据的开始。p的值等于2。
Tobita 和 Kasahara 提出了大量的测试实例,但没有考虑通信延迟和多处理器结构[26]。输入文件可以在 http://www.kasahara.elec.waseda.ac.jp/schedule 上找到。尽管这些问题实例与MSPCD没有直接关系,但我们还是将选定的调度启发式方法应用于包含500个任务的任务图。表7显示了180个实例的最佳调度长度值的平均值,以及四种启发式方法中的每一种得到的结果与该值的偏差(其他启发式方法的偏差范围为10%到200%以上)。值得注意的是,当处理器数量增加时,基于ES的方法的偏差会减少,而基于PPS、LBMC和DC的启发式方法则显示出相反的趋势。这个结果是很自然的,因为前两个启发式方法旨在使用所有可用的处理器,这产生了更高的通信水平。对于DC启发式,当任务显示出较高的通信要求时,大量的处理器证明是有问题的。
我们还提供了应用于本文提出的Set 1问题实例的六个选定的调度启发式方法的完整启发式结果。之前使用的格式和文件名方案也适用于此。每个文件的名称由方法的缩写组成,后面是nonopt,处理器的数量,以及连接拓扑结构和通信问题的指示。例如,CPES.nonopt.p4.comm1.compl.tex表示当多处理器系统包含4个完全连接的处理器并且通信时间很重要时,将CPES调度启发式应用于Set 1例子的结果。相应的结果文件可以在同一网址上找到。
相应的结果文件可以在同一网址上找到。