An adaptive selection approach for the 2D rectangle packing area minimization problem
摘要
本文研究了二维矩形包装面积最小化问题(RPAMP),其目标是将一组矩形包装到一个大小可变的容器中,并使容器的面积最小化。RPAMP被转化为一系列二维条带封装问题(2DSPs)。提出了一种新的自适应选择方法,在每次迭代时选择候选宽度,而不是最初选择最有希望的宽度集。为了避免在同一宽度上花费太多精力,引入了迭代加倍搜索策略。采用基于天际线的最佳拟合启发式算法求解2DSP。与以前的方法相比,本文提出的方法简单得多,因为它不需要任何控制参数。在基准测试集上的计算实验表明,该方法优于现有的所有方法,并改进了大多数实例(39个实例中的28个)的最知名解。特别是对于经过充分研究的Ami33和Ami49实例,该方法找到了更好的解决方案。
一、介绍
在超大规模集成(VLSI)芯片设计领域,通常需要在一个矩形芯片上放置一组矩形模块,这些模块需要通过导线连接。通常考虑的目标是使矩形芯片的面积最小化和导线总长度最小化。如果目标是前者,这个问题通常被称为二维矩形布局面积最小化问题(RPAMP)。RPAMP也可能出现切割和包装问题。例如,在报纸版面或金属或玻璃行业中,需要将较大的板材切割成较小的矩形,以满足客户的需求。
原来如此,另一个优化目标是导线长度最小化。也属于 nesting 问题
形式上,二维矩形布局面积最小化问题可以描述如下。从一个集合 $ R $ 开始,包括 $ n $ 个尺寸为 $ w_i \times h_i,i=1,\cdots,n $ 和一个可变尺寸的矩形容器,目标是固定容器的尺寸(宽度 $ W_c $ 和高度 $ H_c $ ),并将所有矩形正交地装入容器中,以使面积( $ W_c \times H_c $ )最小化。换句话说,需要找到一个最小面积的容器来包装所有的矩形。压缩矩形之间不允许重叠。
切割和包装文献中经常考虑以下约束:
- 方向约束(Orientation constraint):矩形的方向是固定的,即矩形不能旋转。
- 铡刀式切割约束(一刀切)(Guillotine cutting constraint):要求所有的矩形都可以通过铡刀式切割从容器上切割下来,这种切割必须与容器的侧面平行,并将容器切割成两个完全分离的容器。
根据是否考虑这两个约束条件,可以区分RPAMP的四种变体(Bortfeldt,2013):
- OF:矩形的方向是固定的(O),不需要断头台切割(F)。
- RF:矩形可以旋转90度(R),不需要断头台切割(F)。
- OG:矩形的方向是固定的(O),需要断头台切割(G)。
- RG:矩形可以旋转90度◦ (R) ,需要断头台切割(G)。
在本文中,我们只研究变体 RF,这是文献中研究最多的变体。
可以旋转 90 度,不需要满足一刀切。
如果RPAMP中容器的宽度是固定的,则问题将更改为2D条形包装问题(2DSP)。如果容器的宽度和高度都是固定的,并且目标是将矩形尽可能多地装入容器中,那么问题就是二维矩形装箱问题(2DRP)。
玻璃切割就类似 2DSP 问题,装箱问题也挺多的
根据Wäscher等人(2007)对切割和包装问题的改进分类研究,RPAMP是具有两个可变维度的二维矩形开放维度问题,2DSP是二维矩形单变量开放维度问题,2DRP是二维矩形单一大型物体放置问题(SLOPP)或单一背包问题(SKP)。RPAMP也可以被看作是配平损失问题(Dyckhoff等人,1985)。
问题的分类研究
有两种常见的方法用于解决RPAMP。第一种方法使用不同的启发式直接求解RPAMP,第二种方法将RPAMP转换为一系列 2DSPs 或 2DRPs。
具体的方法,估计大家还都是使用第一种比较多。
第一种方法的关键部分是布局表示,即如何表示解决方案。最常见的是Murata等人(1996)提出的序列对(SP)表示,它使用两个序列来说明矩形的关系。后来提出了几种元启发式的SP增强方法,包括模拟退火(SA)(Tang & Wong, 2001; Pisinger, 2007; Chen et al., 2014)、局部搜索(LS)(Janiak et al., 2008)和遗传算法(GA)(Kimura & Ida, 2006; Fernando & Katkoori, 2008)。SP的一个等价表示法是使用两个反义闭合图的反义约束图(TCG)。TCG首先由Lin & Chang(2001)提出,后来由Lin & Chang(2005)和Li等人(2010)研究。此外,O型树(Guo等人,1999;Pang等人,2000;Tang和Sebastian,2005)和B*树(Chang等人,2000;Sun等人,2006;Chen等人,2011)是另外两种最常用的基于树结构的表示法。其他表示方法包括Chen等人(2005)提出的片段列表和Rahim等人(2008)提出的二叉树。Huang和Liu(2006)提出了一个有效的启发式方法,该方法基于所谓的角落占用和最大孔位优先的放置策略。
第二种方法通过固定容器的尺寸,将RPAMP实例转换为一系列2SPS或2DRPs实例。Bortfeldt(2013)和He等人(2015)通过固定容器的宽度和高度,将RPAMP转化为2DRP。这种缩减方法的关键是候选宽度的选择。Bortfeldt(2013)提出了三种变体来生成候选宽度,并通过实验结果选择了最有效的一种。He 等人(2015年)使用相同的策略来选择宽度。固定宽度后,通过设置适当的容器填充率来确定容器的高度。
在切割和包装文献中,2DSP和2DRP都是经过充分研究的问题。针对这两个问题,人们提出了各种基于不同方法的构造性启发式算法。著名的方法包括左下(Baker等人,1980年)、左下填充(Chazelle,1983年)和左下递减(Hopper&Turton,2001年)。Burke等人(2004年)提出了一种使用天际线来表示包装模式的最佳拟合启发式方法。此外,Bortfeldt(2006)提出了一种没有对解进行任何编码的遗传算法。Cui等人(2008)提出了一种考虑一刀切约束的2DSP递归分枝定界算法。He 等人(2012年)提出了一种使用动作空间的高效确定性启发式方法。最近,Wang&Chen(2015)描述了一种剩余空间最大化的包装方法。关于包装问题的其他变体,读者可以参考Cui(2014);胡等(2015);阿隆索等人(2017年)。
基于布局模式的天际线表示,提出了许多改进的最佳拟合(BF)启发式算法。正如¸ık&Özcan(2009)将BF扩展为一种新的双向最佳拟合启发式,Verstichel等人(2013)提出了一种改进的BF启发式。Wei等人(2011)提出了一个包含多个组件的评估函数,以选择最佳位置。Leung等人(2011年)引入了一种新的评分规则来衡量每个矩形的大小。后来,杨等人(2013年)建议改进评分规则,魏等人(2016年)进一步改进评分规则。最近,Wei等人(2017)提出了一种增强的基于天际线的启发式算法,并给出了有效的实现。
在本文中,我们提出了一种适用于RPAMP的自适应选择方法(ASA)。ASA通过固定容器的宽度将RPAMP转换为一系列 2DSPs。ASA在每次迭代中随机选择一个可能的宽度,而不是最初固定一组有希望的宽度。将自适应地更新每个待选择宽度的概率,以确保在给定更高概率的情况下,宽度可能会导致更好的RPAMP解决方案。基于天际线的启发式算法适用于求解2DSP。
本文有三个主要贡献。首先,我们提出了一种无需任何控制参数的自适应选择方法来解决RPAMP问题。与以前的策略相比,我们的方法更加简单,易于实现。其次,我们采用了基于天际线的启发式算法来求解2DSP,并使用迭代加倍策略来提高效率。最后,在基准测试集上的结果表明,我们的方法优于所有现有方法,并为大多数实例找到了新的最佳解决方案。
论文的其余部分组织如下。第2节描述了所提出的自适应选择方法的细节。第3节给出了求解2DSP的随机局部搜索。第4节报告了该方法的计算实验。最后,第5节对本文进行了总结。
二、ASA算法
Bortfeldt(2013)和He等人(2015)通过固定容器的宽度将RPAMP转换为一系列2DSPs,然后通过固定高度将 2DSP 转换为 2DRP。由于输入矩形的每个维度组合都可能是 2DSP 的候选宽度,因此可能的候选宽度通常太多。因此,求解每个宽度上的 2DSP 需要花费太多时间。因此,这种缩减方法的关键部分是如何选择最有希望的候选宽度,从而获得高质量的RPAMP解决方案。Bortfeldt(2013)和He等人(2015)首先从所有可能的宽度中选择了一些给定数量(Bortfeldt(2013)中的150个和He等人(2015)中的100个)的有希望的宽度,然后仅对所选宽度的2DSP进行了求解。
Bortfeldt(2013)提出了三种变体来生成一组有希望的宽度。首先,只考虑给定范围 $ [W_{min},W_{max}] $ 内的宽度。 $ W_{min} $ 是所有矩形较小尺寸中的最大值, $ W_{max} $ 设置为 $ \left\lfloor\alpha \cdot \operatorname{area}(R)^{1 / 2}\right\rfloor $ ,其中 $ area(R) $ 是 R 中所有矩形的面积总和, $ \alpha $ 是略大于 $ 1 $ 的参数(Bortfeldt(2013)和He等人(2015)中为 $ 1.2 $ ,在我们的实现中为 $ 1.05 $ )。
在第一个变体 $ WV1 $ 中, $ nw $ 等距宽度值从 $ [W_{min},W_{max}] $ 范围中选择, $ nw $ 是所考虑的宽度数。
第一种确定宽度的方式
而在第二个变体 $ WV2 $ 中,对于 $ [W_{min}, W_{max}] $ 范围内的每一个宽度,2DSP 的一个实例被解决(由Bortfeldt(2006)提出的建设性启发式BFDH*)。然后根据解的密度从大到小排序,并选择前 $ nw $ 个宽度。Bortfeldt(2013)假设导致最佳2DSP解决方案的宽度是关于其整个启发式搜索的适当宽度。
在 $ WV2 $ 中,需要对2DSP进行两种算法。第一个算法用于评估宽度,并根据评估结果选择最有希望的宽度。第二个算法是对所选择的宽度进行调用,以找到最佳的RPAMP解决方案。由于第一个算法是对每一个可能的宽度进行调用,所以它不能太耗时,简单的建设性启发式方法是一个不错的选择。由于所选宽度的大小通常较小,一个更复杂的搜索方法可以作为第二种方法。 $ WV2 $ 的假设是,使用第一种方法导致最佳RPAMP解决方案的宽度值,也能导致使用第二种方法的最佳RPAMP解决方案。然而,通常很难找到这样的两种算法。Bortfeldt(2013)表明,使用他们选定的算法的 $ WV2 $ 是无效的。经过对一些测试数据的初步实验,我们发现使用我们的算法, $ WV2 $ 也是无效的。
第二种确定宽度的方式,没有什么用处
以被研究得很透彻的Ami33实例为例。对于每个候选宽度,我们通过将iter设置为1和n(矩形的数量),分别调用我们的2DSP求解器RandomLS(见第3节,第8行被修改为尝试每个排序规则,而不是选择一个)两次。RandomLS是一个随机局部搜索程序,iter 是用来控制迭代次数的参数。因此,通过设置iter为1,RandomLS可以被看作是一种建设性的启发式方法。图1显示了RandomLS在Ami33的每个宽度上得到的解决方案的填充率,其中X轴是候选宽度,Y轴是填充率。从图中可以看出,当iter设置为1时,导致最佳填充率的宽度,在iter设置为n时,将不会导致最佳填充率。
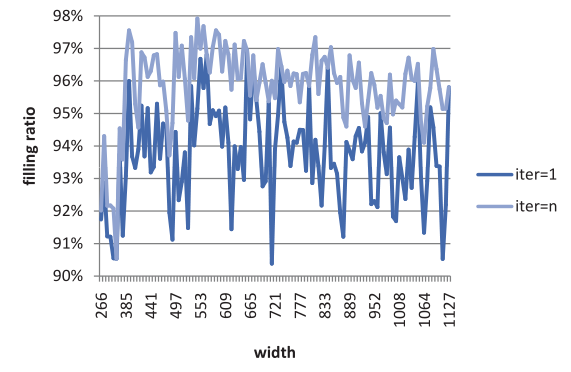
iter=1的最佳宽度并不适用于iter=n的
在最后一个变体 $ WV3 $ 中,通过宽度 $ w $ 的频率 $ f(w) $ 来选择有希望的宽度。 $ w $ 的频率被定义为 $ w $ 的尺寸组合的数量。 $ w $ 的尺寸组合被定义为一组矩形尺寸 $ (w_i 或 h_i,i \in 1,\cdots,n) $ 之和为 $ w $ 。那么对于 $ n $ 个矩形,总共会有 $ 2 C_{n}^{1}+2^{2} C_{n}^{2}+\cdots+2^{n} C_{n}^{n} $ 个不同的尺寸组合。例如,假设有 $ 2 $ 个尺寸为 $ 1\times2 $ 和 $ 3\times4 $ 的矩形,那么,有 $ 2C_1^2 + 2^2C_2^2 = 8 $ 种尺寸组合,分别是{1}、{2}、{3}、{4}、{1,3}、{1,4}、{2,3}和{2,4}。这8组的尺寸之和分别为1、2、3、4、4、5、5 和 6。因此,1、2、3、4、5和6的频率分别为1、1、1、2、2和1。正如Bortfeldt(2013)所证明的,宽度 $ w \in [W_{min}, W_{max}] $ 的所有维度组合都可以通过伪多项式复杂度的动态编程产生。
这个公式,代表着,从 $ n $ 个矩形中选出 $ i $ 个矩形,每个矩形有宽和高两维,因此为 $ 2^i \times C_n^i $ ,看来需要计算这个频率。
作者认为,通过输入矩形的尺寸最频繁地组合宽度,将导致高质量的RPAMP解决方案。将 $ [W_{min}, W_{max}] $ 中的所有宽度按照频率降序排序,并选择前 nw 个宽度。Bortfeldt(2013)通过实验结果表明,变体 $ WV3 $ 比其他两种表现更好。He等人(2015)在他们的动态缩减方法中也使用了 $ WV3 $ 。
第三种方法,有点ASA的意思了。
当矩形的数量相对较少时,频率是一种有用的方法,可以选择最有希望的宽度。然而,随着矩形数量的增加,在省略 $ f(w) $ 等于 0 的宽度和 $ [W_{min}, W_{max}] $ 范围内的几个最小数字后, $ f (w) $ 成为 $ w $ 的增加函数。图2描绘了省略 $ f(w) $ 等于 $ 0 $ 的宽度后,实例Ami33在 $ [W_{min}, W_{max}] $ 范围内各宽度的频率。我们可以看到,当 $ w $ 大于 700 时, $ f (w) $ 随着 $ w $ 的增大而增大。因此,选择频率最大的 nw 宽度通常等于选择频率大于 0 的最大 nw 宽度。然而,如图1所示,导致最佳填充率的宽度不一定是最大的。
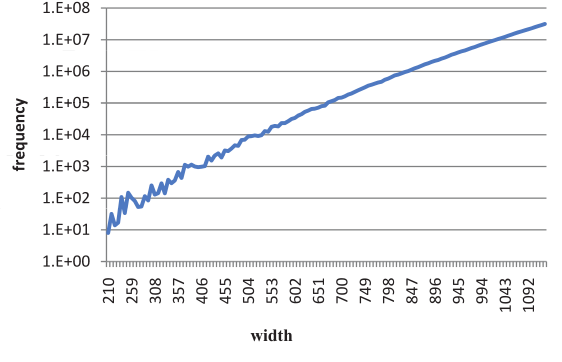
上述分析表明,在开始时很难选择最有希望的宽度。因此,我们在本文中提出了一个替代方法。我们不在一开始就选择最有希望的候选宽度,而是在一开始就不对宽度进行过滤。更确切地说,所有可能的宽度将被添加到候选宽度集中,并且在每次迭代时从这个集合中随机选择一个宽度。为了选择可能导致高质量RPAMP解决方案的宽度,我们给每个宽度打分,以衡量这个宽度被选中的概率。这个分数是基于在这个宽度上调用RandomLS得到的最佳解决方案的填充率,并将被自适应地更新。每个宽度的初始分数被设置为调用RandomLS得到的解决方案的填充率,并将 iter 设置为 1。在每次迭代中,根据分数随机选择一个宽度(分数越高,获得的概率越大),在所选择的宽度上调用2DSP求解器RandomLS,该宽度的分数也会相应更新。为了避免在同一个宽度上花费太多精力,我们通过最初将iter设置为1,并在每次迭代后将iter增加一倍的方式来迭代用于同一个宽度的精力。
使用了迭代加深,避免时间过长
自适应选择方法如算法1所示,程序 RandomLS 是 2DSP 的随机局部搜索方法。与Bortfeldt(2013)的方法类似,我们只考虑给定范围 $ [W_{min}, W_{max}] $ 内的宽度。同时,我们放弃那些不代表输入矩形的尺寸组合的宽度。因此, $ W $ 只包含输入矩形的尺寸组合的宽度。

对于每个 $ W_i $ ,一个变量 $ H_i $ 用来记录在这个宽度上发现的最小高度, $ f r_i $ 是相应的填充率。此外,一个变量 $ iter_i $ 被用来记录在 $ W_i $ 上最后一次调用RandomLS时使用的值, $ iter_i $ 最初被设置为 $ 1 $ 。首先,我们对 $ W $ 中的每一个宽度调用RandomLS,并将 $ iter $ 设置为1,然后, $ W $ 中的宽度以填充率进行升序排列。在每次迭代中,从 $ W $ 中随机选择一个宽度,选择第 $ k $ 个宽度的概率由 $ \frac{2k} {|W|×(|W|+1)} $ 计算,这使得 $ W $ 中序号较大的宽度的概率更高。假设选择的宽度是 $ W_k $ ,它首先将 $ iter_k $ 加倍,然后在 $ W_k $ 上调用RandomLS, $ iter $ 设置为 $ iter_k $ 。在RandomLS返回后,如果有必要,将更新 $ H_k $ 、 $ fr_k $ 和 $ W $ 。 $ iter_k $ 的最大值被限制为 $ n $ ,以避免在一次调用RandomLS时进行过多的迭代。
算法1的讲解,因为是按照填充率升序排列的,因此序号大的选择的概率大,填充率也更大,比较合理。搜索之后, $ H_i $ 可能会更小了,填充率变高了,因此需要调整 $ W_i $ 的位置。(可以直接二分,然后 swap)
变量 $ iter_k $ 在每次调用宽度 $ W_k $ 之前都会翻倍,以确保在相同的宽度上花费比以前更多的精力。原因是随着程序的处理,改进解决方案的难度加大,所以需要更多的迭代来让RandomLS找到更好的解决方案。然而,为了避免在相同的宽度上花费太多的精力, $ iter_k $ 的最大值被限制在矩形的数量 $ n $ 。
三、2DSP的随机局部搜索
随机局部搜索RandomLS程序是用来解决2DSP的。 RandomLS是一个基于序列的随机局部搜索程序,它使用 best-fit 启发式打包程序Heuristic Packing(第3.2节)来构建一个放置方案。更确切地说,给定一个序列 $ R $ ,容器的宽度 $ W_k $ 和控制参数 $ iter $ ,RandomLS调用HeuristicPacking 函数 $ iter $ 次,最后返回发现的最小高度。
第二步,针对选中的宽度,使用
HeuristicPacking(R, Wk, iter)找到最小高度Hk

对于每个 $ W_k $ ,RandomLS维护一个包含排序规则集的全局集合 $ sr_k $ (实际就是一个有序的集合)。如果是第一次在宽度 $ W_k $ 上调用RandomLS,RandomLS将首先按如下方式初始化集合 $ sr_k $ 。它使用四个排序规则来生成四个初始序列,并在每个序列上调用HeuristicPacking,然后将每个排序规则加入 $ sr_k $ 中。之后, $ sr_k $ 按照HeuristicPacking返回的高度递减的顺序进行排序。否则,它从 $ sr_k $ 中随机选择一个排序规则。第 $ i $ 条排序规则以 $ \frac{2i}{|srk|×(|srk|+1)} $ 的概率被选中,然后由选中的排序规则生成一个初始序列。在初始序列的基础上,通过随机局部搜索,进行若干次迭代来改进解决方案。在每个迭代中,它通过交换R中随机选择的两个矩形来生成一个新的序列R0,并对R0调用HeuristicPacking。只有当R0的解不比R差时,R才会被R0取代;否则,R0就会被放弃。上述迭代重复 $ iter $ 次。最后,我们更新集合 $ sr_k $ ,确保它按高度的递减顺序排序,并返回最终发现的最小高度。
在我们的实现中使用了以下四个排序规则。
- 按面积递减排序;
- 按高度递减排序;
- 按宽度递减排序;
- 随机排序。
其中第四条规则用于生成一个随机序列,使搜索空间多样化。
3.1 基于skyline的best-fit启发法
算法3给出的HeuristicPacking是一个基于天际线的最佳拟合启发法,改编自Wei等人(2016)的方法。HeuristicPacking是一个基于序列的构建过程。更具体地说,该启发式使用空间来表示包装模式,这与Burke等人(2004)介绍的天际线基本相同。
给定一个矩形序列R和容器的宽度 $ W_c $ ,HeuristicPacking将矩形一个接一个地排列。最后返回包装结果的最终高度。在每一步中,它首先从天际线中选择最左下角的线段 $ s $ ,然后使用评分规则(第3.2节)选择最适合的矩形,并将选择的矩形放置在 $ s $ 处,天际线相应地被更新。
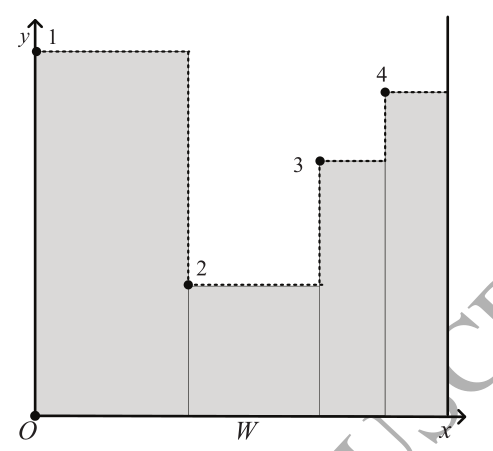
在我们的方法中,当前的放置模式由一条直线天际线表示,它是一组连续的垂直线段的轮廓线。图3给出了一个天际线的例子,其中每个线段 $ s_j $ 在其左端点被标记为 $ j $ (以左端点为序号)。最初的空放置模式由对应于容器底部的一条线段表示。HeuristicPacking总是选择最左下角的线段 $ s $ 作为候选线段来放置一个矩形。矩形的左下角放在 $ s $ 的左端点上,或者右下角放在 $ s $ 的右端点上。如果有一个以上的矩形可以放入 $ s $ ,它将使用评分规则(第3.2节)选择最合适的矩形 $ r $ 。在选定的矩形 $ r $ 被放在 $ s $ 处后,天际线将被更新。一个与 $ r $ 的顶边相对应的新线段被添加,而受影响的现有线段也被更新。图4(a)给出了将矩形 $ r $ 放在 $ s_2 $ 处后的更新天际线。如果没有可以放在 $ s $ 处的矩形, $ s $ 就会被提升到其下级邻居的高度。在图3中,如果没有矩形可以放置在所选段 $ s_2 $ 处,天际线将被更新,如图4(b)所示。图4(b)中的阴影区域被视为废物,不会在以后的阶段中使用。
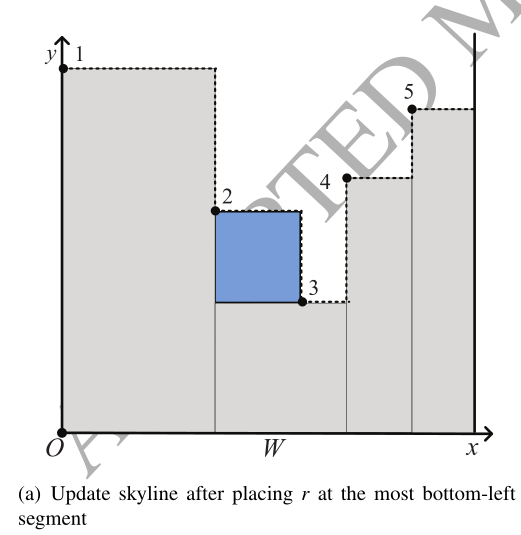
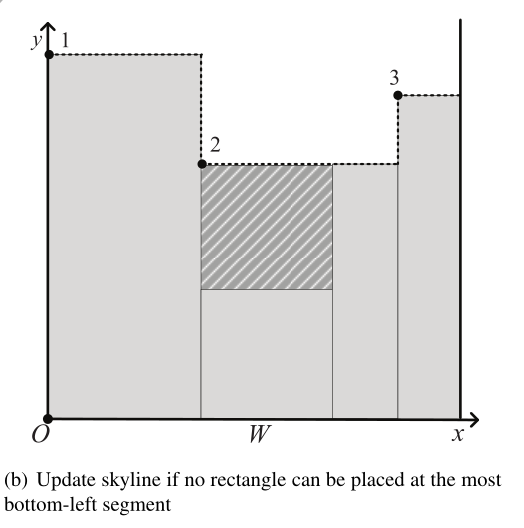
3.2 评分规则
假设当前最左下角的区段为 $ s $ ,其左(右)邻居的高度为 $ h_l $ ( $ h_r $ ),对于每个适合于 $ s $ 的矩形,如果 $ h_l \ge h_r $ ,可分为八种情况(见图5)。如果 $ h_l \lt h_r $ ,也有八种情况类似。HeuristicPacking选择得分最高的矩形,如果出现平局,则选择 R 中的第一个矩形。由于本文中的矩形是可旋转的,对于每个矩形 $ r $ ,在试图将其放置在 $ s $ 处时都会尝试两种方向,较高的分数被定义为 $ r $ 的分数。我们的评分规则可以被视为Leung等人(2011)提出的评分规则的延伸。
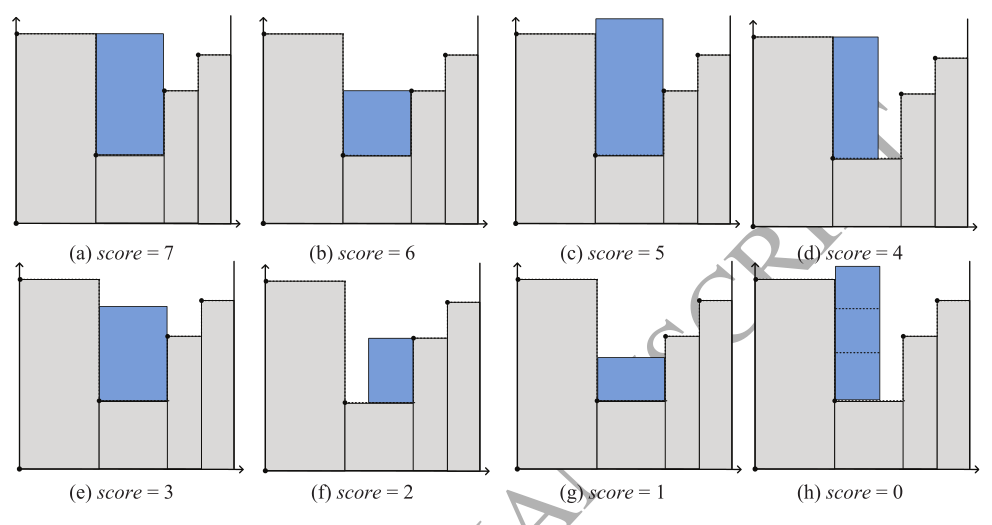
这个评分规则没有用函数的形式表达,使用的是 if 的形式。
其实不是8种,底边完全覆盖的有5种,不完全覆盖的也有5种(h有三种)。
四、实验
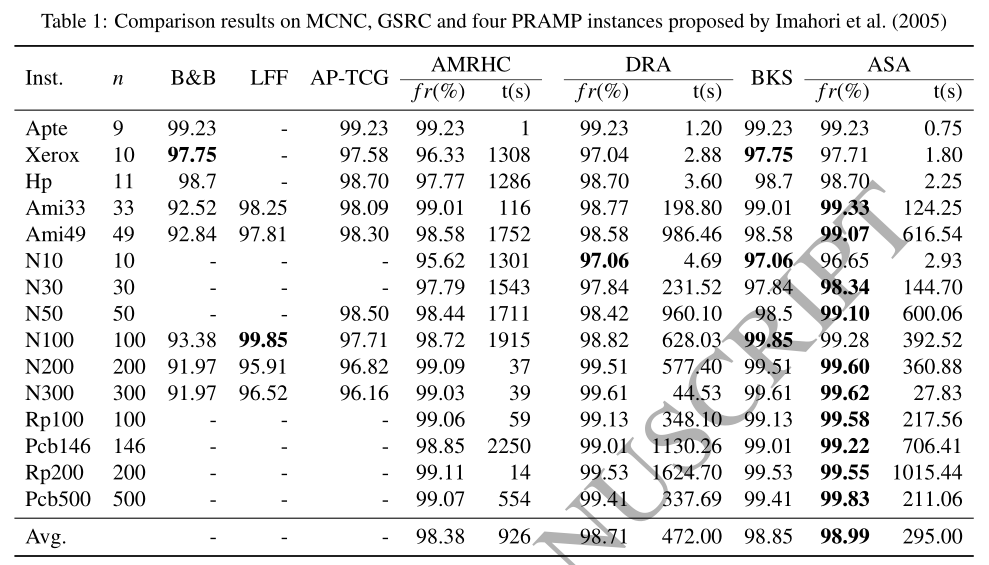
适应性选择方法(ASA)是使用Visual C++ 6.0作为顺序算法实现的。所有的实验都是在一台装有Intel(R) Xeon(R) CPU E5645 2.40 GHz和3.49 GB内存的Windows电脑上进行的。参数 $ α $ 被设置为1.05,这样可以在一个填充率为90.70% 的正方形中计算出一个最优解。两组来自文献的实例被用来测试ASA的性能。第一组有15个实例,包括经典的 VLSI 楼层规划实例MCNC(北卡罗来纳州微电子中心)、GSRC(千兆级系统研究中心)和Imahori等人(2005)提出的4个RPAMP实例(表1中 Rp100 到 Pcb500 )。表1中的实例Apte到Ami49属于MCNC,而实例N10到N300属于GSRC。第二组(在表2中给出)包括Bortfeldt(2013)最近提出的24个RPAMP实例。
ASA与RPAMP的5种代表性算法进行了比较:
- B&B:Chan & Markov (2004)的一个分支和边界算法。对于小型实例Apte、Xerox 和 HP,B&B 找到了最优解。对于其他较大的实例,B&B被修改为一个可扩展的分层启发式算法,不一定能产生最优解。
- LFF:Wu&Chan(2005)提出的改进的LestflexibilityFirst启发式算法。
- AP-TCG:Li等人(2010)提出的统一的非切割区域预判转闭图算法。
- AMRHC:Bortfeldt(2013)提出的面积最小化减少启发式组合程序。
- DRA:He等人(2015)的动态减法启发式
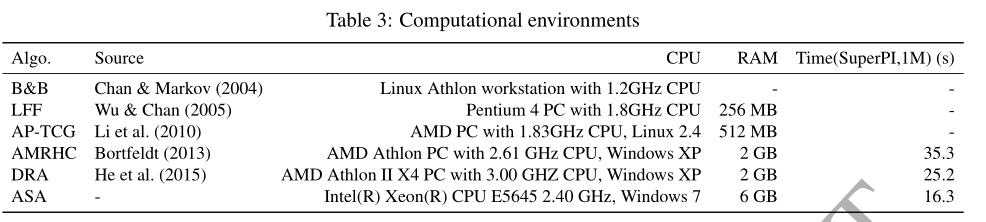
我们选择这些方法是因为它们是迄今为止最强的解决方案方法。第一组中的一个实例的当前最著名的解决方案至少可以通过其中一种方法找到。请注意,Bortfeldt(2013)的结果适用于变体RG,而其他方法的结果适用于变体RF。表3总结了每种方法的计算环境,其中计算机运行SuperPi所用的时间(1M)(http://www.superpi.net/)列在第五列中。
就我们所知,DRA是文献中最先进的算法。因此,我们主要在以下方面将ASA与DRA进行比较。我们的计算机大约比DRA快1.6(25.3/16.3)倍。为了进行公平的比较,我们将ASA的每个实例的时间限制设定为DRA所用时间的1/1.6。请注意,所有被比较的算法都只运行一次,因此,通过设置随机种子为1,ASA也运行了一次。在下文中,我们比较了每个实例的填充率,其中填充率被定义为所有矩形的总面积与容器面积的比率。所有的实例和ASA获得的每个实例的详细结果都可以在www.villagerwei.com。
4.1 测试数据的结果
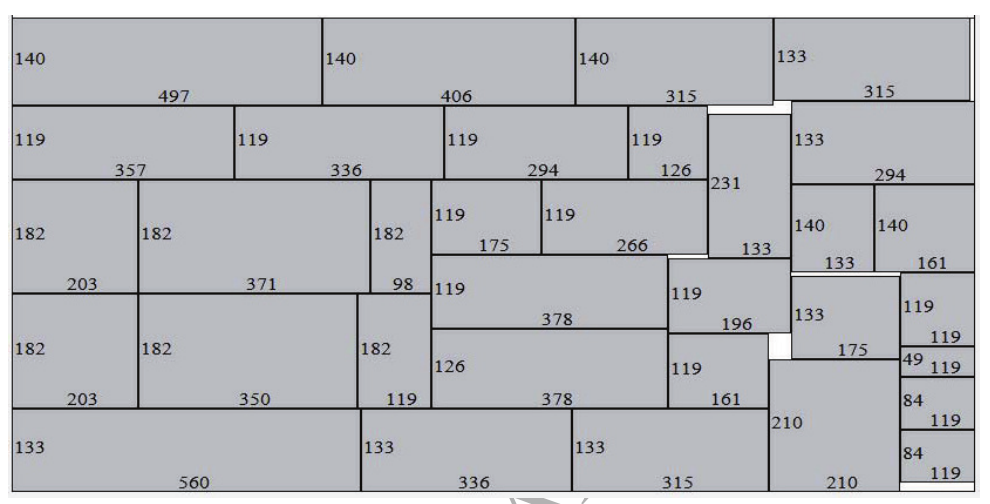
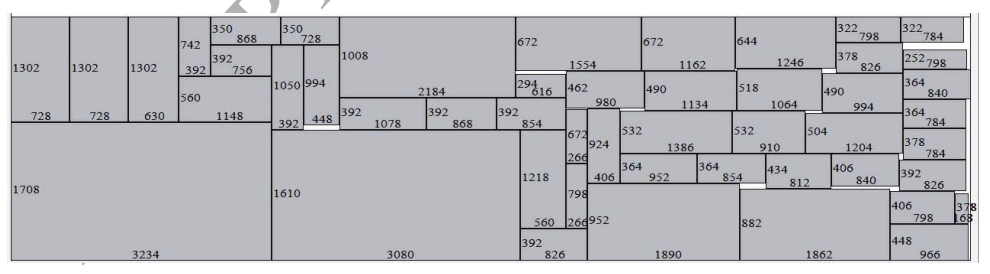
表1给出了第一组的比较结果,其中每个方法下的一栏给出了每个实例的填充率(破折号表示没有给出结果),较好的结果用粗体字标出。BKS一栏给出了每个实例的最佳解决方案。对于AMRHC、DRA和ASA的方法, $ fr(\%) $ 列表示填充率, $ t(s) $ 列给出计算时间。行 $ Avg. $ 是这组中所有实例的平均结果。该表显示,ASA改善了10个实例的BKS,并与2个实例(Apte和Hp)的BKS相符。只有Xerox, N10和N100的例子,ASA的结果比BKS的结果差。平均而言,ASA将BKS提高了0.14%。即使是对于已经研究过的实例Ami33和Ami49,ASA也能找到更好的解决方案,填充率分别为99.33%和99.07%。图6和图7分别显示了ASA在Ami33和Ami49实例上找到的布局。请注意,布局被旋转了 $ 90^{\circ} $ 以使图形更清晰。与DRA相比,ASA在12个实例上的表现优于DRA。只有在N10实例上,DRA的解决方案优于ASA的解决方案。平均来说,ASA比DRA好 $ 0.28% $ 。
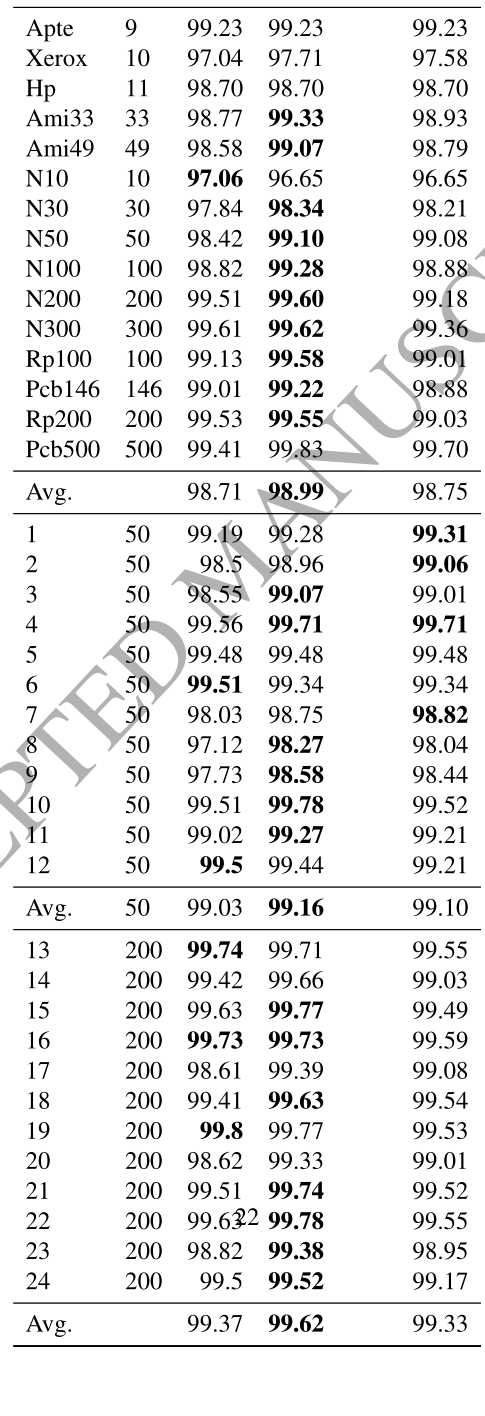
表2给出了第二组的比较结果。两行Avg.是这组实例中第一和最后12个实例的平均结果。根据Bortfeldt(2013)生成这些实例的方法,前12个实例是强异质性的,而其他12个实例是弱异质性的。此外,前12个实例是用50个矩形生成的,而其他12个实例有200个矩形。对于所有这24个实例,ASA在18个实例中得到了更好的结果,在2个实例中与BKS相匹配。在平均填充率方面,ASA对前12个实例的BKS提高了0.13%,对后12个实例的BKS提高了0.16%。

4.2 收敛行为

请记住,ASA的时间限制被设置为DRA每个实例的 $ 1/1.6 $ 的时间。为了测试ASA的收敛行为,对于每个实例,ASA被执行了 $ 3600 $ 秒,并记录了每一秒后的最佳发现的解决方案。结果绘制成图8,其中x轴是时间,y轴是当时的最佳发现方案的填充率。请注意,x轴的值是按指数增长的,实例被分为三组,其中Set1是第一个测试集,Set2-1和Set2-2是第二个测试集的第一个和最后一个12个实例。图中显示,ASA对所有这些测试集的收敛速度很快,ASA在很短的时间内就获得了高质量的解决方案。此外,在大多数情况下,当花费更多的时间时,改进仍在继续,尽管改进的速度在不断降低。因此,ASA可以满足不同场景下的不同要求。
4.3 参数 $ \alpha $ 的影响
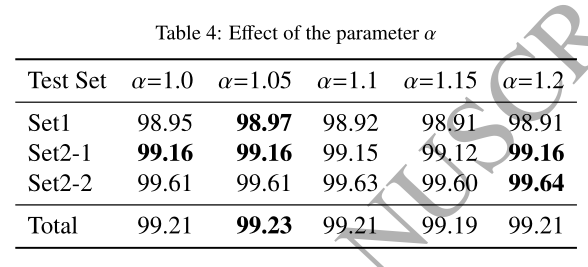
为了测试参数 $ \alpha $ 的影响,我们通过设置 $ \alpha $ 为不同的值1.0、1.05、1.1、1.15和1.2来运行方法。每组的平均结果总结为表4,其中黑体字表示更好的结果。结果表明, $ \alpha = 1.05 $ 产生了最好的结果。然而,不同数值的结果之间的差异非常小。因此,我们选择1.05作为最终值。
4.4 适应性选择策略的效果
为了测试自适应选择策略的效果,我们修改了我们的方法,使用Bortfeldt(2013)和He等人(2015)使用的第三个变体 WV3 来选择有希望的宽度。首先,将 $ [W_{min}, W_{max}] $ 中的所有宽度按照频率降序进行排序。然后,我们逐一调用 RandomLS 的每一个宽度。我们继续使用迭代加倍的策略。更确切地说,我们在第一次调用RandomLS时,将参数 $ iter $ 设置为 $ 1 $ 。在下一次迭代中,我们将把参数 $ iter $ 翻倍,并在每个宽度上再次调用RandomLS。迭代过程不断重复,直到超过时间限制。修改后的方法被表示为ASA + WV3。比较结果如表5所示。ASA + WV3的结果比DRA的结果好一点,但比ASA的结果差一点。这表明了自适应选择策略原始启发式对ASA的成功的重要性。
五、结论
本文研究了二维矩形包装面积最小化问题,其中的目标是将一组矩形包装到一个尺寸可变的容器中,并使容器的面积最小。我们没有直接解决RPAMP,而是将其改为一系列的二维带状包装问题。一个自适应过程被用来动态地选择最有希望的二维条带的宽度。为了避免在同一宽度上花费太多时间,它迭代地将花费在每个宽度上的努力加倍。一个简单的基于天际线的启发式方法被用来解决2DSP问题。在标准基准上的实验结果显示了所提方法的有效性和效率。未来可能的工作之一是将自适应选择方法应用于楼层规划问题的其他变体。