J. 灵能传输
题目描述:
给出一个数组 $ n $ 个元素,对于 $ i \in [2, n - 1] $ 有以下两种操作
- 如果 $ a_i \ge 0 $ , $ a_{i-1} + a_i, a_i - 2 \times a_i, a_{i + 1} + a_i $
- 如果 $ a_i \lt 0 $ , $ a_{i-1} - |a_i|, a_i + 2 \times |a_i|, a_{i + 1} - |a_i| $
进行若干次操作,使得 $ max_{i = 1}^n|a_i| $ 最小,输出最小值
数据范围:
$ 1\le T \le 3, 3 \le n \le 3\times 10^5 \\\\ |a_i| \le 10 ^ 9 $
题解:
这个题目转化很关键,如果看到标签,就会简单许多。
首先这个表示形式可以进行统一: $ a_{i-1} + a_i, a_i - 2 \times a_i, a_{i + 1} + a_i $ ,观察对前缀和序列的影响
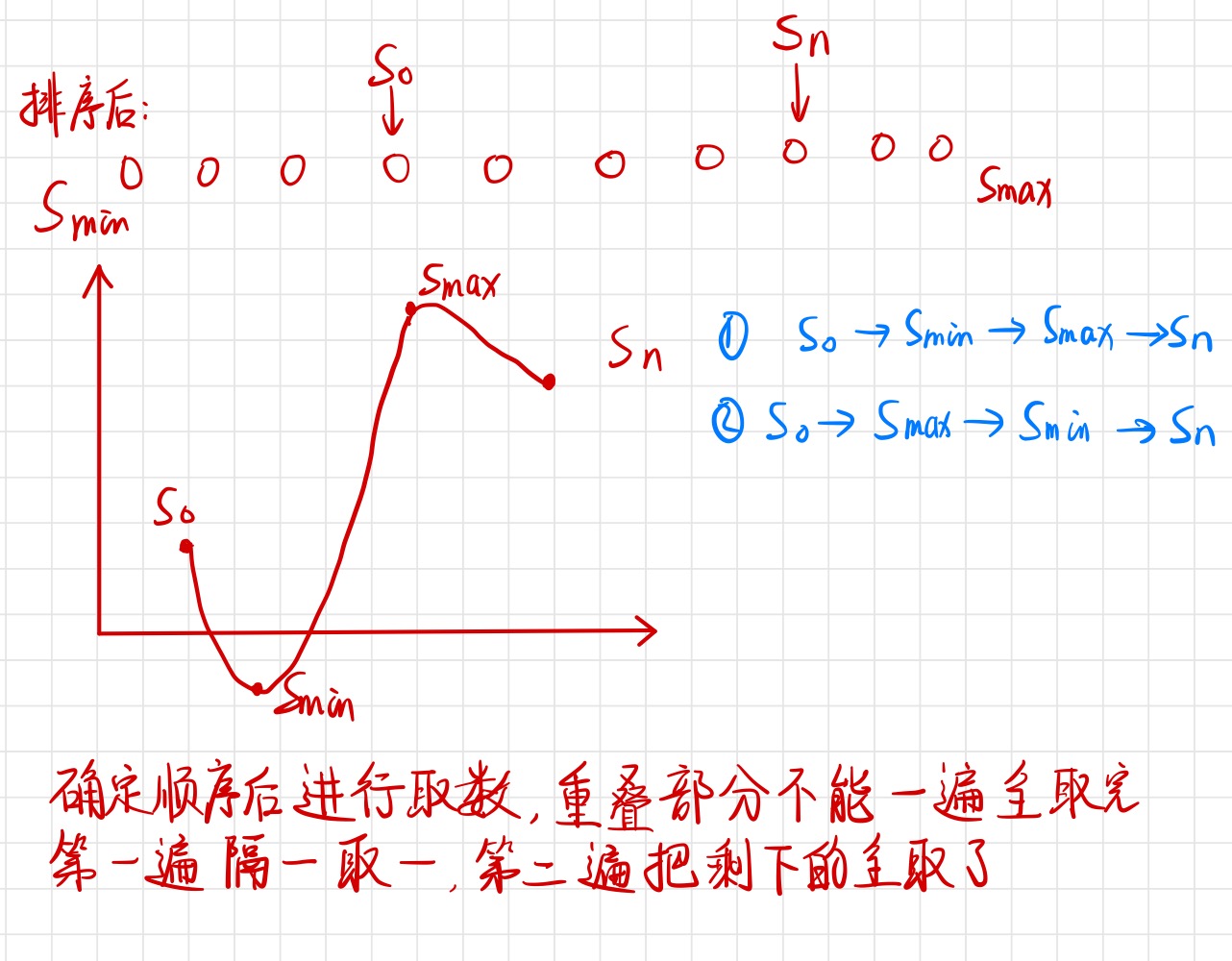
发现这个操作实际上是对前缀和序列进行两项交换 $ (s_i, s_{i-1}) $ ,由于题目中给出的下标范围,所以是不涉及 $ s_n $ 的。通过交换 $ s_i $ 得到最后的序列,然后相邻的作差得到实际序列。加入 $ s_0 = 0 $ ,补全一致性, $ s_0 $ 是起点, $ s_n $ 是终点。一个贪心的想法就是将所有的元素 $ s_i $ 直接排序,然后从起点到终点找到一种方式可以遍历所有的元素。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| #include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
#define ll long long
using namespace std;
const int mod = 1e4;
const int maxn = 3e5 + 10;
int n, m, k;
ll sum[maxn];
bool flag[maxn];
ll ans[maxn];
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
ios::sync_with_stdio(false);
cin.tie(0);
int tcase;
cin >> tcase;
while(tcase--)
{
cin >> n;
sum[0] = 0;
for(int i = 1,x; i <= n; i++)
{
cin >> x;
sum[i] = x + sum[i-1];
flag[i] = flag[i - 1] = 0;
}
ll s0 = 0, sn = sum[n];
if(s0 > sn) swap(s0, sn);
int index0, indexn;
sort(sum, sum + 1 + n);
for(int i = 0; i <= n; i++)
{
if(sum[i] == s0) index0 = i;
if(sum[i] == sn) indexn = i;
}
int l = 0, r = n;
for(int i = index0; i >= 0; i -= 2)
{
ans[l++] = sum[i], flag[i] = 1;
}
for(int i = indexn; i <= n; i += 2)
{
ans[r--] = sum[i], flag[i] = 1;
}
for(int i = 0; i <= n; i++)
{
if(!flag[i]) ans[l++] = sum[i];
}
ll maxx = 0;
for(int i = 1; i <= n; i++)
{
maxx = max(abs(ans[i] - ans[i - 1]), maxx);
}
cout << maxx << endl;
}
return 0;
}
|
