Luobuyu's Blog

0%

G.Human Pyramid

发表于 分类于 ， 热度： ℃ 评论：
本文字数： 918 阅读时长 ≈ 1 分钟
数字三角形，需要使用DP，然后还需要斜着看

G.Human Pyramid

题目描述：

s 个 A 种人，剩下全是 B 种人，搭建 h 层人形金字塔。A 种人可以踩在 B 种人的身上，反之不可以。每种人内部都是相同的，问有多少种方案数。

数据范围：
$ 1\le h \le 100, 0 \le s\le \frac{1}{2}h(h + 1) $

题解：

看到数字三角形，方案数，首先想到了 DP 。笑死，根本不会 D .

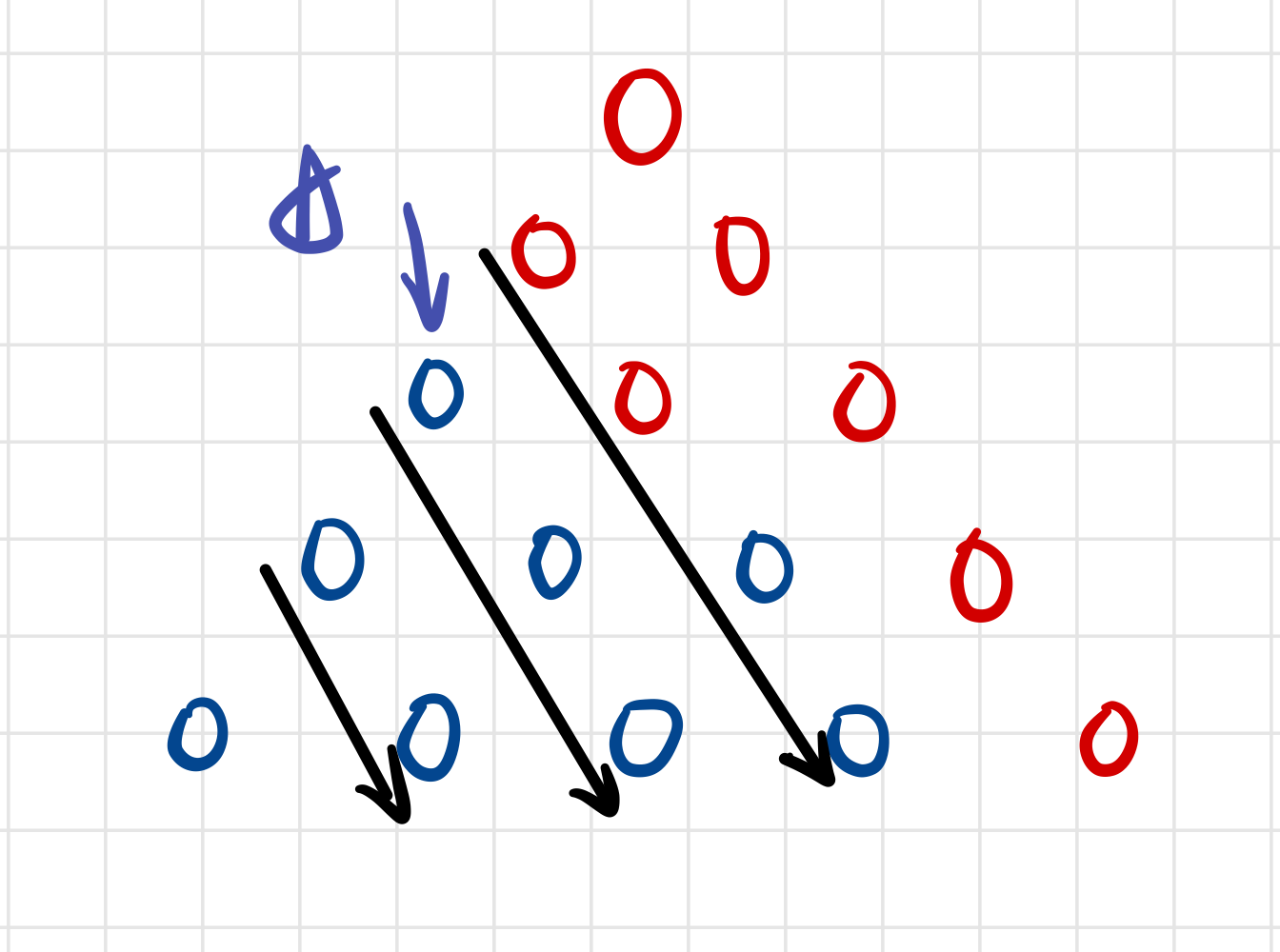
PNG图像 2

可以发现，如果斜着某一列出现了一个 B ，则以该点为顶点的三角形全是 B 。而且该列的 B 必定是从下往上连续的。

设状态：

设状态 dp(i, j, k) 表示高度 i ，前 i 行（斜着看）总共有 j 个 B ，第 i 行至少有 k 个 B 的方案数。

找递推：

由于至少有 k 个 $ = $ 至少有 k + 1 个 $ + $ 恰好有 k 个

所以 $ dp(i, j, k) = dp(i, j, k + 1) + dp(i-1, j - k, k - 1) $

第 i 行使用 k 个时，第 i-1 行使用 k-1 个才满足

由递推方程可以得到循环顺序，i, j 正着遍历，k 倒着遍历

注意 k 的起点，首先 $ k \le j $ ，然后第 i 行最多有 i 个，所以 $ k \le min(i, j) $

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
const int maxn = 1e2 + 10;
const int maxm = 1e5 + 10;
int h, s;
ll dp[maxn][maxn * maxn / 2][maxn];
int main()
{
// #define COMP_DATA
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    read(h, s);
    dp[0][0][0] = 1;
    for (int i = 1; i <= h; i++)
    {
        for (int j = 0; j <= s; j++)
        {
            int k = min(i, j); // k这列最大值就为 i,另外还肯定要满足 k <= j
            for (; k >= 0; k--)
            {
                dp[i][j][k] = dp[i][j][k + 1] + dp[i - 1][j - k][max(k - 1, 0)];
                dp[i][j][k] %= mod;
            }
        }
    }
    cout << dp[h][s][0] << endl;
    return 0;
}