Luobuyu's Blog

0%

2021-icpc-nerc

发表于 分类于 ， 热度： ℃ 评论：
本文字数： 11k 阅读时长 ≈ 10 分钟
一场final题，只能签签到。很多题都需要记录方案，时限都比较足，记录方案需要注意下

B. Button Lock

题目描述：

一个密码锁，上面有 $ d $ 个按键，还有一个 Reset 键。现在给出 $ n $ 个可能的密码，请问至少需要按多少次才能把所有的密码试一遍，按 reset 也算一次。

数据范围：
$ 1\le d \le 10, 1\le n \le 2^d - 1 $

题解：

题解中使用了二分图匹配，不太容易想到

建图，如果密码 $ i $ 是 $ j $ 的子集，则连一条边 $ i \rightarrow j $ 的有向边，转化为了用不相交的路径覆盖所有的顶点，一条路径的代价是该路径最后一个密码 $ 1 $ 的个数加上 $ 1 $ (因为需要使用 reset)

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
#include <bits/stdc++.h>
#define ll long long
#define lll long long
using namespace std;
namespace FAST_IO
{
    inline char nextChar()
    {
        static char buf[1000000], *p1 = buf, *p2 = buf;
        return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++;
    }
#define getch getchar
    template <class T>
    inline void read(T &x)
    {
        T flag = 1;
        x = 0;
        char ch = getch();
        while (ch < '0' || ch > '9')
        {
            if (ch == '-')
                flag = -1;
            ch = getch();
        }
        while (ch >= '0' && ch <= '9')
        {
            x = (x << 3) + (x << 1) + (ch ^ 48), ch = getch();
        }
        x *= flag;
    }

    template <class T, class... _T>
    inline void read(T &x, _T &...y)
    {
        return read(x), read(y...);
    }

    inline void print128(lll x)
    {
        if (x < 0)
            putchar('-'), x = -x;
        if (x > 9)
            print128(x / 10);
        putchar(x % 10 + '0');
    }

    void FIO()
    {
        ios::sync_with_stdio(false);
        cin.tie(0);
    }

} // namespace FAST_IO
using namespace FAST_IO;
const ll mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF_LL = 0x3f3f3f3f3f3f3f3f;
const double eqs = 1e-5;
const int maxn = 1e4 + 10;
const int maxm = 1e5 + 10;
int t, n, m, k;
int d;
int a[maxn];
int match[maxn];
bool vis[maxn];
vector<int> g[maxn];
vector<int> v;
bool cmp(int x, int y)
{
    return __builtin_popcount(x) > __builtin_popcount(y);
}

bool find(int x)
{
    for (int i = 0; i < g[x].size(); i++)
    {
        int v = g[x][i];
        if (!vis[v])
        {
            vis[v] = 1;
            if (!match[v] || find(match[v]))
            {
                match[v] = x;
                return true;
            }
        }
    }
    return false;
}
int main()
{
// #define COMP_DATA
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    FIO();
    cin >> d >> n;
    string s;
    for (int i = 1; i <= n; i++)
    {
        cin >> s;
        for (int j = d - 1; j >= 0; j--)
        {
            a[i] = a[i] * 2 + (s[j] - '0');
        }
    }

    sort(a + 1, a + 1 + n, cmp);
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j < i; j++)
        {
            if ((a[i] & a[j]) == a[i])
                g[i].push_back(j);
        }
    }

    for (int i = 1; i <= n; i++)
    {
        memset(vis, 0, sizeof(vis));
        find(i);
    }

    memset(vis, 0, sizeof(vis));
    for (int i = 1; i <= n; i++)
    {
        if (!vis[i])
        {
            int x, y;
            vis[i] = 1;
            v.push_back(-1);
            int pre = a[i], pos = match[i];
            while (pos)
            {
                vis[pos] = 1;
                int cur = a[pos];
                for (int j = 0; j < d; ++j)
                {
                    if (((pre ^ cur) >> j) & 1)
                        v.push_back(j);
                }
                pre = cur;
                pos = match[pos];
            }
            for (int j = 0; j < d; ++j)
            {
                if ((pre >> j) & 1)
                    v.push_back(j);
            }
        }
    }

    cout << v.size() - 1 << endl;
    while (v.size() > 1)
    {
        int x = v.back();
        v.pop_back();
        if (x == -1)
            cout << "R ";
        else
            cout << x << " ";
    }
    cout << endl;
    return 0;
}

D. Digits

题目描述：

给出 $ n $ 个正整数，从中选出尽量多的数，相乘得到的乘积末尾是 $ d $ 。输出选择的个数和选择的数字

数据范围：
$ 1\le n \le 10^5, 0 \le d \le 9, 1\le a_i \le 1000 $

题解：

很明显需要进行 $ dp $ ，由于 $ 1\le a_i \le 1000 $ ，所以需要取对数，使用 $ double $ ，另外需要得到方案，记录方案比较麻烦。其实可以参考背包问题，因为这个题目设计状态 $ dp[i][j] $ 表示前 $ i $ 个中选出尽量多的数后乘积末尾为 $ j $ 的乘积值，集合划分 $ dp[i][j] $ 来自于 $ a[i] ，dp[i-1]p ， dp[i-1][j] $ 。也是选与不选的关系，如果选的话有两种，一种是从 $ dp[i-1][p] $ 选 $ a[i] $ 过来，另一种是前面的都没有，直接选 $ a[i] $ ；不选的话就是 $ dp[i-1][j] $ 。

参考：背包问题记录方案

  • 记录 $ pre[i][j] $ 是否选了 $ i $ ， $ pre[i][j] = 1 $ 代表选了 $ i $ ，同时容量 $ j $ 减去 $ v[i] $ 得到前一个，然后看是否选了前一个
  • 第一种方法的递归形式
  • 不使用 $ pre $ 直接判断 $ dp[i][j] $ 和 $ dp[i + 1][j - v[i]] + w[i] $ 的关系，其实和第一种方法差不多

总的来说，都是记录当前位是否选择，和前一个状态 $ (i, j) $

这里可以使用同样的方法，使用 $ Node( use, i, j) $ 来表示， $ use = 1 $ 代表选中了 $ i $ ， $ (i, j) $ 表示的是前一个（就是从哪一个转移过来的），这样就解决了。

但是这个题可能数据比较拉，也可以使用我提出的方法，直接向前面查，实测得到 $ dp $ 数组后，使用判断就可以得到方案，不用使用搜索，也是挺快的。

代码：

往前查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include <bits/stdc++.h>
#define ll long long
namespace FAST_IO
{

    inline char nextChar()
    {
        static char buf[1000000], *p1 = buf, *p2 = buf;
        return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++;
    }
#define getch getchar
    template <class T>
    inline void read(T &x)
    {
        T flag = 1;
        x = 0;
        char ch = getch();
        while (ch < '0' || ch > '9')
        {
            if (ch == '-')
                flag = -1;
            ch = getch();
        }
        while (ch >= '0' && ch <= '9')
        {
            x = (x << 3) + (x << 1) + (ch ^ 48), ch = getch();
        }
        x *= flag;
    }

    template <class T, class... _T>
    inline void read(T &x, _T &...y)
    {
        return read(x), read(y...);
    }
} // namespace FAST_IO
using namespace std;
using namespace FAST_IO;
const ll mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF_LL = 0x3f3f3f3f3f3f3f3f;
const double eqs = 1e-5;
const int maxn = 1e5 + 10;
const int maxm = 1e5 + 10;
int t, n, m, k;
int d;
int a[maxn];
long double dp[maxn][10];
vector<int> ans;
// 迷惑，改成long double就过了，改成 double 第一个样例都过不去
int main()
{
// #define COMP_DATA
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    read(n, d);
    for (int i = 1; i <= n; i++)
    {
        read(a[i]);
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 0; j < 10; j++)
        {
            dp[i][j] = 0;
        }
    }
    dp[1][a[1] % 10] = log(a[1]);
    for (int i = 1; i <= n; i++)
    {
        dp[i][a[i] % 10] = log(a[i]);
        for (int j = 0; j < 10; j++)
        {
            if (dp[i - 1][j] == 0)
                continue;
            dp[i][j] = max(dp[i][j], dp[i - 1][j]);
            dp[i][j * a[i] % 10] = max(dp[i - 1][j] + log(a[i]), dp[i][j * a[i] % 10]);
        }
    }
    if (dp[n][d] == 0)
    {
        printf("-1\n");
    }
    else
    {
        bool flag;
        for (int i = n; i >= 1; i--)
        {
            if (dp[i][d] == dp[i - 1][d])
                continue;
            ans.push_back(a[i]);
            flag = false;
            for (int j = 0; j < 10; j++)
            {
                if (j * a[i] % 10 == d && dp[i - 1][j] + log(a[i]) == dp[i][j * a[i] % 10])
                {
                    d = j;
                    flag = true;
                    break;
                }
            }
            if (!flag)
                break;
        }
        printf("%d\n", ans.size());
        for (int i = 0; i < ans.size(); i++)
        {
            printf("%d ", ans[i]);
        }
        printf("\n");
    }
    return 0;
}

使用 $ pre $ 记录方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
#include <bits/stdc++.h>
#define ll long long
#define lll long long
namespace FAST_IO
{

    inline char nextChar()
    {
        static char buf[1000000], *p1 = buf, *p2 = buf;
        return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++;
    }
#define getch getchar
    template <class T>
    inline void read(T &x)
    {
        T flag = 1;
        x = 0;
        char ch = getch();
        while (ch < '0' || ch > '9')
        {
            if (ch == '-')
                flag = -1;
            ch = getch();
        }
        while (ch >= '0' && ch <= '9')
        {
            x = (x << 3) + (x << 1) + (ch ^ 48), ch = getch();
        }
        x *= flag;
    }

    template <class T, class... _T>
    inline void read(T &x, _T &...y)
    {
        return read(x), read(y...);
    }

    inline void print128(lll x)
    {
        if (x < 0)
            putchar('-'), x = -x;
        if (x > 9)
            print128(x / 10);
        putchar(x % 10 + '0');
    }

} // namespace FAST_IO
using namespace std;
using namespace FAST_IO;
const ll mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF_LL = 0x3f3f3f3f3f3f3f3f;
const double eqs = 1e-5;
const int maxn = 1e5 + 10;
const int maxm = 1e5 + 10;
int t, n, m, k, d;
double dp[maxn][10];
struct Node
{
    bool use;
    int x, y;
} pre[maxn][10];
int a[maxn];
vector<int> ans;
int main()
{
// #define COMP_DATA
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    read(n, d);
    for (int i = 1; i <= n; i++)
    {
        read(a[i]);
    }
    for (int i = 1; i <= n; i++)
    {
        dp[i][a[i] % 10] = log(a[i]);
        pre[i][a[i] % 10] = {true, -1, a[i] % 10};
        for (int j = 0; j < 10; j++)
        {
            if (dp[i - 1][j])
            {
                // 不选
                if (dp[i][j] < dp[i - 1][j])
                {
                    dp[i][j] = dp[i - 1][j];
                    pre[i][j] = {false, i - 1, j};
                }
                // 选
                if (dp[i - 1][j] + log(a[i]) > dp[i][j * a[i] % 10])
                {
                    dp[i][j * a[i] % 10] = dp[i - 1][j] + log(a[i]);
                    pre[i][j * a[i] % 10] = {true, i - 1, j};
                }
            }
        }
    }
    if (dp[n][d] == 0)
        printf("-1\n");
    else
    {
        int lastn = n, lastd = d;
        Node tmp;
        do
        {
            tmp = pre[lastn][lastd];
            if (tmp.use)
            {
                ans.push_back(a[lastn]);
            }
            // 注意不能直接lastn = pre[lastn][lastd].x,
            // 因为会导致lastn变了，导致lastd不正确
            lastn = tmp.x;
            lastd = tmp.y;
        } while (tmp.x != -1);
        printf("%d\n", ans.size());
        for (auto x : ans)
        {
            printf("%d ", x);
        }
        printf("\n");
    }

    return 0;
}

G. Guide

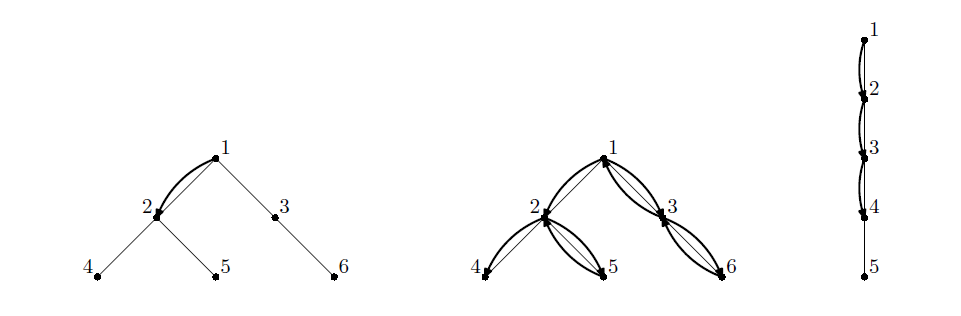
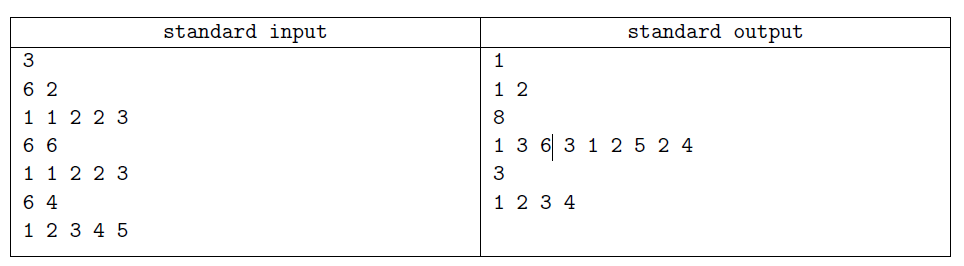
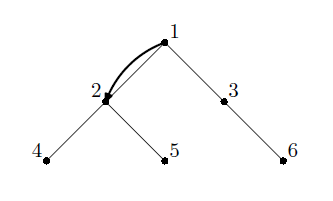
题目描述：

给出一棵树 $ n $ 个结点，边权为 $ 1 $ ，从根节点出发访问 $ k $ 个结点的最小花费和访问顺序。

数据范围：
$ 1\le T \le 100, 1\le k \le n \le 100 $

image-20210410231429055

image-20210410231633756

题解：

注意一下，上图中的第二个，明显发现有的只需要访问一次，有的需要访问两次。因此只需要访问一次的边最多就行，可以发现，只要访问最长的链即可。首先找出最长的链，假设 $ dep[1] = 0 $ ，则当 $ k >= depmax + 1 $ ， $ ans = depmax + (k - depmax - 1) \times 2 $ ，当 $ k \lt depmax + 1 $ ， $ ans = k - 1 $ 。记录方案才是需要关注的。观察样例发现访问序列是欧拉序，因此可以直接对每一个最长链上的点进行 $ dfs $ ，得到欧拉序

image-20210410232132276

欧拉序：

  • dfs到加进，dfs回加进，每个点总共加入度遍 1, 2, 4, 2, 5, 2, 1, 3, 6, 3, 1
  • dfs进加进，dfs最后一次回加进，每个点总共加两遍 1, 2, 4, 4, 2, 5, 5, 2, 1, 3, 6, 6, 3, 1

image-20210410233314659

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
#include <bits/stdc++.h>
#define ll long long
#define lll long long
namespace FAST_IO
{

    inline char nextChar()
    {
        static char buf[1000000], *p1 = buf, *p2 = buf;
        return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1000000, stdin), p1 == p2) ? EOF : *p1++;
    }
#define getch getchar
    template <class T>
    inline void read(T &x)
    {
        T flag = 1;
        x = 0;
        char ch = getch();
        while (ch < '0' || ch > '9')
        {
            if (ch == '-')
                flag = -1;
            ch = getch();
        }
        while (ch >= '0' && ch <= '9')
        {
            x = (x << 3) + (x << 1) + (ch ^ 48), ch = getch();
        }
        x *= flag;
    }

    template <class T, class... _T>
    inline void read(T &x, _T &...y)
    {
        return read(x), read(y...);
    }

    inline void print128(lll x)
    {
        if (x < 0)
            putchar('-'), x = -x;
        if (x > 9)
            print128(x / 10);
        putchar(x % 10 + '0');
    }

} // namespace FAST_IO
using namespace std;
using namespace FAST_IO;
const ll mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF_LL = 0x3f3f3f3f3f3f3f3f;
const double eqs = 1e-5;
const int maxn = 1e2 + 10;
const int maxm = 1e5 + 10;
int t, n, m, k;
vector<int> g[maxn];
vector<int> lon;
vector<int> ans;
bool flag[maxn];
int dep[maxn];
void init()
{
    ans.clear();
    lon.clear();
    for (int i = 1; i <= n; i++)
    {
        g[i].clear();
        flag[i] = 0;
    }
}
void getDep(int u, int fa)
{
    dep[u] = dep[fa] + 1;
    for (int i = 0; i < g[u].size(); i++)
    {
        int v = g[u][i];
        if (v == fa)
            continue;
        getDep(v, u);
    }
}

void getLongest(int u, int fa)
{
    for (int i = 0; i < g[u].size(); i++)
    {
        int v = g[u][i];
        if (v == fa)
            continue;
        if (dep[v] == dep[u] - 1)
        {
            lon.push_back(v);
            flag[v] = true;
            getLongest(v, u);
        }
    }
}

void dfs(int u, int *cot, int fa)
{
    ans.push_back(u);
    if ((*cot) == 0)
        return;
    for (int i = 0; i < g[u].size(); i++)
    {
        int v = g[u][i];
        if (flag[v] || v == fa)
            continue;
        (*cot)--;
        dfs(v, cot, u);
        ans.push_back(u);
        if ((*cot) == 0)
            break;
    }
}

int main()
{
// #define COMP_DATA
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    int tcase;
    read(tcase);
    while (tcase--)
    {
        cin >> n >> k;
        init();
        for (int i = 1, x; i < n; i++)
        {
            read(x);
            g[x].push_back(i + 1);
            g[i + 1].push_back(x);
        }
        dep[0] = -1;
        getDep(1, 0);
        int maxdep = -1, index = -1;
        for (int i = 1; i <= n; i++)
        {
            if (dep[i] > maxdep)
            {
                maxdep = dep[i];
                index = i;
            }
        }
        lon.push_back(index);
        flag[index] = true;
        getLongest(index, 0);
        reverse(lon.begin(), lon.end());
        if (maxdep + 1 >= k)
        {
            // cout << k - 1 << endl;
            printf("%d\n", k - 1);

            for (int i = 0; i < k; i++)
            {
                printf("%d%c", lon[i], " \n"[i == k - 1]);
            }
        }
        else
        {
            int extra = k - maxdep - 1;
            int fa = -1;
            for (int i = 0; i < lon.size(); i++)
            {
                if (extra != 0)
                {
                    dfs(lon[i], &extra, fa);
                }
                else
                {
                    ans.push_back(lon[i]);
                }
            }
            int ansv = maxdep + (k - maxdep - 1) * 2;
            printf("%d\n", ansv);
            for (int i = 0; i < ans.size(); i++)
            {
                printf("%d ", ans[i]);
            }
            printf("\n");
        }
    }
    // ans = dep + (k - dep - 1) * 2
    return 0;
}