Luobuyu's Blog

0%

nowcoder多校(第七场)

发表于 分类于 ， 热度： ℃ 评论：
本文字数： 8.3k 阅读时长 ≈ 8 分钟
2020年nowcoder暑期多校训练(第七场)，签到签的太慢了，又碰到了那种题，不用推公式的在那浪费时间推公式

A. Social Distancing

题目描述：

在一个半径为 $ r $ ，圆心为 $ (0, 0) $ 的圆内整点放置 $ n $ 个人，使得两两距离的平方和最大

数据范围：
$ 1\le T \le 250 $

$ 1\le n \le 8, 1\le r \le 30 $

题解：

居然是个 $ dp $ 题。考虑使用 $ dp $ 打表， $ dp[i][j][k] $ 为放置了 $ i $ 个点，横坐标和为 $ j $ ，纵坐标和为 $ k $ 的情况下的答案。

维护第一项的值，枚举 $ j,k $ 去更新 $ dp $ 值，用数组 $ ans[i][r] $ 来更新在半径为rr的圆，放置了 $ i $ 个点的答案， $ ans[i][r]=max\{i×dp[i][j][k]−j^2−k^2\} $

打一下表，直接输出就行

代码：

打表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <bits/stdc++.h>
#define ll long long
#define pii pair<int, int>
using namespace std;
const int maxn = 500 + 10;
const ll mod = 1e9 + 7;
const int base = 303;
ll n, t, m, k;

vector<pii> q;

int dis(int x, int y)
{
    return x * x + y * y;
}
int dis(pii x)
{
    return x.first * x.first + x.second * x.second;
}

bool cmp(pii a, pii b)
{
    return dis(a) < dis(b);
}

int dp[10][maxn][maxn];
int ans[10][40];
int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    for(int i = -30; i <= 30; i++)
    {
        for(int j = -30; j <= 30; j++)
        {
            if(dis(i, j) <= 30 * 30)
            {
                q.push_back({i, j});
            }
        }
    }

    sort(q.begin(), q.end(), cmp);
    memset(dp, -1, sizeof(dp));
    dp[0][base][base] = 0;
    for(int r = 1; r <= 30; r++)
    {
        for(int now = 0; now < q.size(); now++)
        {
            auto x = q[now];
            if(dis(x) > r * r) break;
            for(int i = 1; i <= 8; i++)
            {
                for(int j = base - r * i; j <= base + r * i; j++)
                {
                    for(int k = base - r * i; k <= base + r * i; k++)
                    {
                        if(~dp[i-1][j-x.first][k -x.second])
                        {
                            dp[i][j][k] = max(dp[i][j][k], dp[i-1][j-x.first][k -x.second] + dis(x));
                        }
                    }
                }
            }
        }

        for(int i = 1; i <= 8; i++)
        {
            for(int j = base - r * i; j <= base + r * i; j++)
            {
                for(int k = base - r * i; k <= base + r * i; k++)
                {
                    if(~dp[i][j][k])
                    {
                        int t1 = j - base, t2 = k - base;
                        ans[i][r] = max(ans[i][r], i * dp[i][j][k] - dis(t1, t2));
                    }
                }
            }
        }
    }

    for(int i = 1; i <= 8; i++)
    {
        for(int j = 1; j <= 30; j++)
        {
            printf("%d,", ans[i][j]);
        }
        printf("\n");
    }
    return 0;
}

得到数据输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <bits/stdc++.h>
#define ll long long
#define pii pair<int, int>
using namespace std;
const int maxn = 500 + 10;
const ll mod = 1e9 + 7;
const int base = 303;
int n, t, m, k, r;

int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    int ans[8][30] = {
    0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
    4,16,36,64,100,144,196,256,324,400,484,576,676,784,900,1024,1156,1296,1444,1600,1764,1936,2116,2304,2500,2704,2916,3136,3364,3600,
    8,32,76,130,224,312,416,554,722,896,1064,1248,1512,1746,2016,2264,2600,2888,3218,3584,3912,4344,4712,5138,5612,6062,6536,6984,7520,8084,
    16,64,144,256,400,576,784,1024,1296,1600,1936,2304,2704,3136,3600,4096,4624,5184,5776,6400,7056,7744,8464,9216,10000,10816,11664,12544,13456,14400,
    24,96,218,384,624,880,1188,1572,2014,2496,2984,3520,4224,4870,5616,6336,7224,8056,9008,9984,10942,12080,13144,14326,15624,16896,18184,19488,20968,22480,
    36,144,324,576,900,1296,1764,2304,2916,3600,4356,5184,6084,7056,8100,9216,10404,11664,12996,14400,15876,17424,19044,20736,22500,24336,26244,28224,30276,32400,
    48,192,432,768,1224,1740,2356,3102,3954,4896,5872,6960,8280,9564,11016,12456,14160,15816,17666,19584,21500,23688,25808,28122,30624,33120,35664,38266,41200,44076,
    64,256,576,1024,1600,2304,3136,4096,5184,6400,7744,9216,10816,12544,14400,16384,18496,20736,23104,25600,28224,30976,33856,36864,40000,43264,46656,50176,53824,57600,
    };
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d %d", &n, &r);
        n--, r--;
        printf("%d\n", ans[n][r]);
    }
    return 0;
}

B. Mask Allocation

题目描述：

$ n \times m $ 个物品怎么分配打包，可以随意将包裹组合得到 $ n $ 组每组 $ m $ 个和 $ m $ 组每组 $ n $ 个

数据范围：
$ 1\le T \le 100 $

题解：

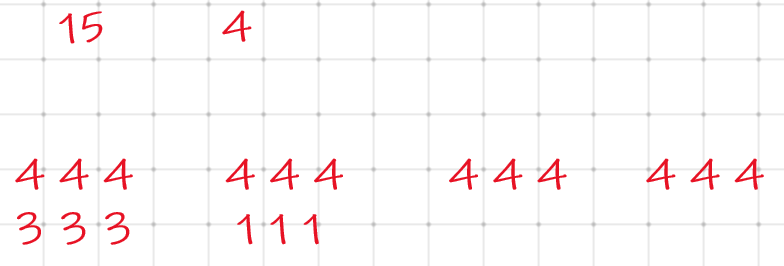
image-20200801224126763

看到这组就应该知道需要递推了，可怜我还在不断的尝试。其实也快想到正解了。我构造的也是前面 $ m - m \% n $ 个 $ n $ ，后面的搞错了直接填上 $ n $ 个 $ m\%n $ 了，没有看到是递推的。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 500 + 10;
const ll mod = 1e9 + 7;
int n, t, m, k;
vector<int> ans;
void solve(int n, int m)
{
    if(n == 0)
    {
        printf("%d\n", k);
        for(auto x : ans)
        {
            printf("%d ", x);
        }
        printf("\n");
        return;
    }
    int tmp = m % n;
    k += m - tmp;
    for(int i = 1; i <= m - tmp; i++)
    {
        ans.push_back(n);
    }
    solve(tmp, n);
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d%d", &n, &m);
        k = 0;
        if(n > m) swap(n, m);
        ans.clear();
        solve(n, m);
    }
    return 0;
}

C.

题目描述：

数据范围：

题解：

代码：

1
2


D. Fake News

题目描述：

前 $ n $ 项平方和是否是一个完全平方数

数据范围：
$ 1\le T \le 10^6 $

$ 1\le n \le 10^{15} $

题解：

实测 $ python $ 在输入输出情况下， $ 1s $ 跑不完 $ 1e6 $ ，甚至跑不完 $ 1e5 $

只有为 $ 1 $ 和 $ 24 $ 才是。果然推公式就会白给

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 500 + 10;
ll t, n;
int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    scanf("%lld", &t);
    while (t--)
    {
        scanf("%lld", &n);
        if (n == 1 || n == 24)
        {
            printf("Fake news!\n");
        }
        else
        {
            printf("Nobody knows it better than me!\n");
        }
    }
    return 0;
}

E.

题目描述：

数据范围：

题解：

代码：

1
2


F.

题目描述：

数据范围：

题解：

代码：

1
2


G.

题目描述：

数据范围：

题解：

代码：

1
2


H. Dividing [除法分块]

题目描述：

定义 legend tuple

  • $ (1, k) $ $ true $
  • $ (n, k) $ $ -> $ $ (n+k, k), (n\times k, k) $

给出 $ N, K $ 求出有多少组 $ (n,k) $ $ 1\le n \le N, 1\le k \le K $

数据范围：
$ 1\le N, K \le 10^{12} $

$ \mod{1e9 + 7} $

题解：

只有一组数据，只是数据比较大。对 $ k $ 进行分组， $ [1,K] $ ，对于每个 $ k $ 求出在 $ N $ 内有多少组。满足 $ n\%k == 1 || n\%k == 0 $

使用除法分块 $ \sqrt{n} $ 计算这个求和

1
2
3
4
5
6
7
8
9
10
11
ll divfloor(ll n, ll k)
{
    ll l = 2, r, ret = 0;
    while(l <= k && l <= n)
    {
        r = min(n / (n / l), k);
        ret = (ret + (r - l + 1) % mod * (n / l) % mod) % mod;
        l = r + 1;
    }
    return ret;
}

计算 $ \sum_{k = 2}^{K}\lfloor \frac{N}{k} \rfloor $ 使用上面的除法分块方法。分成每个区间去求，每个区间内的 $ \lfloor \frac{N}{k} \rfloor $ 全部一样

$ l $ 区间左端点，则这段区间的值为 $ \lfloor \frac{N}{l} \rfloor $ ，下面需要求区间右端点。结果仍为 $ \lfloor \frac{N}{l} \rfloor $ 的最大的 $ l $ 即为右端点 $ r $ 。记 $ \lfloor \frac{N}{l} \rfloor $ 为 $ x $

即：

而且 $ y_2 $ 一定是最小的一个了。 $ y_1 \ge x $ 说明可以抽出几个 $ x $ 放到 $ l $ 中得到 $ r $ ，所以可以明显看出 $ r = \lfloor \frac{N}{x} \rfloor $ ，下一个区间的左端点为 $ r + 1 $

由于 $ k \gt N $ 时全是 $ 0 $ ，所以直接取 $ min $ ，不考虑那一部分了

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 500 + 10;
const ll mod = 1e9 + 7;
ll n, t, m, k;

ll divfloor(ll n, ll k)
{
    ll l = 2, r, ret = 0;
    while(l <= k && l <= n)
    {
        r = min(n / (n / l), k);
        ret = (ret + (r - l + 1) % mod * (n / l) % mod) % mod;
        l = r + 1;
    }
    return ret;
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    scanf("%lld %lld", &n, &k);
    printf("%lld\n", ((divfloor(n, k) + divfloor(n - 1, k)) % mod + n + k - 1)%mod);
    return 0;
}

I.

题目描述：

数据范围：

题解：

代码：

1
2


J. Pointer Analysis

题目描述：

一个程序中有 $ 26 $ 个对象, 每个对象有 $ 26 $ 个成员指针变量. 同时还有 $ 26 $ 个普通的指针变量. 给定 $ n $ 条赋值语句, 询问在以任意顺序执行每条语句无限多次的过程中, 每个指针变量可能指向的对象集合.

数据范围：
$ 1\le N \le 200 $

题解：

大模拟

直接暴力求解，只有这四种情况，每种情况遍历一遍判断一下。

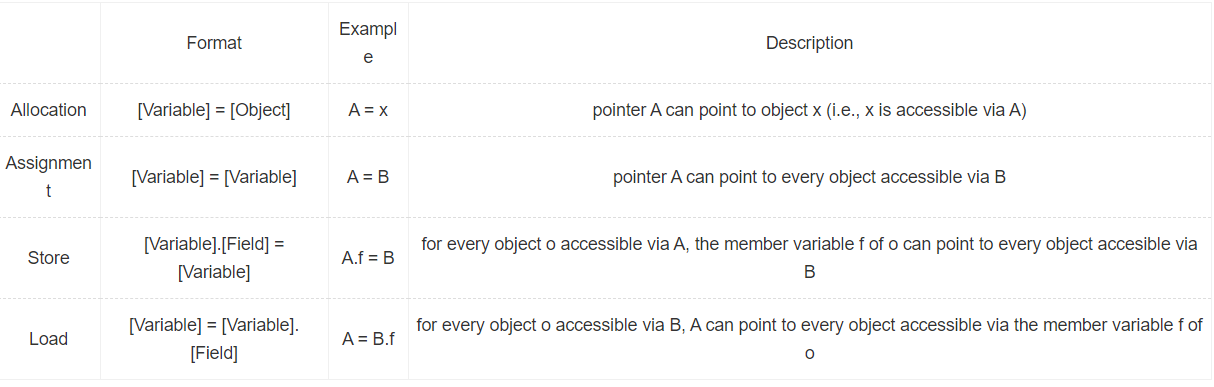
image-20200802204232439

使用 $ ans[i][j] $ 用来记录大写字母对应的对象，使用 $ int $ 直接进行或运算就可以传递。使用 $ a[i][j][k] $ 用来表示成员变量对应的大写字母对应的对象

读入的时候使用 $ \%*s $ 可以规避一些字符

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include <bits/stdc++.h>
#define ll long long
#define pii pair<int, int>
using namespace std;
const int maxn = 20 + 10;
const int maxm = 200 + 10;
const ll mod = 1e9 + 7;
const int base = 303;
int n, t, m, r;
int ans[maxn][maxn], a[maxn][maxn][maxn];
char s1[maxm][maxn], s2[maxm][maxn];
int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
    {
        scanf("%s%*s%s", s1[i]+1, s2[i]+1);
    }
    for(int p = 1; p <= n; p++)
    {
        for(int i = 1; i <= n; i++)
        {
            int len1 = strlen(s1[i]+1), len2 = strlen(s2[i]+1);
            int c1 = s1[i][1] - 'A';
            int c2 = s2[i][1] - 'A';
            if(len1 == len2)
            {
                // A = x
                if(s2[i][1] >= 'a') ans[c1][s2[i][1]-'a'] = 1;
                else // A = B
                {
                    for(int j = 0; j < 26; j++)
                    {
                        ans[c1][j] |= ans[c2][j];
                    }
                }
            }
            else if(len2 >= 3)
            {
                // A = B.f
                int c3 = s2[i][3] - 'a';
                for(int j = 0; j < 26; j++)
                {
                    if(ans[c2][j])
                    {
                        for(int k = 0; k < 26; k++)
                        {
                            ans[c1][k] |= a[c3][j][k];
                        }
                    }
                }
            }
            else
            {
                // A.f = B
                int c3 = s1[i][3] - 'a';
                for(int j = 0; j < 26; j++)
                {
                    if(ans[c1][j]) // s1 可以指向 j 对象(非空)
                    {
                        for(int k = 0; k < 26; k++)
                        {
                            a[c3][j][k] |= ans[c2][k];
                        }
                    }
                }
            }
        }
    }
    for(int i = 0; i < 26; i++)
    {
        printf("%c: ", 'A' + i);
        for(int j = 0; j < 26; j++)
        {
            if(ans[i][j]) printf("%c", 'a' + j);
        }
        printf("\n");
    }
    return 0;
}