A.
题目描述：
题解：
代码：
题目描述：
给出一个函数
给出一些 $ (n_i, c_i) $ ，求 $ f_{c_i}(n_i) mod(1e9+7) $
数据范围：
$ T(1≤T≤1e6) $ $ 1\le n_i,c_i \le 10^6 $
题解：
观察可以发现， $ f_c(x) = c^{x质因子个数} $
数据比较大，使用筛一下，求解即可
代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| #include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
typedef long long ll;
const int maxn = 1e6 + 10;
const ll mod = 1e9 + 7;
int t;
ll n, c, d;
ll qpow(ll a, ll b, ll mod)
{
ll ans = 1, tmp = a;
while(b)
{
if(b & 1) ans = ans * tmp % mod;
tmp = tmp * tmp % mod;
b >>= 1;
}
return ans % mod;
}
int prime[maxn];
bool notPrime[maxn];
int cnt = 0, num[maxn];
int from[maxn];
void sieve(int n)
{
for(int i = 2; i <= n; i++)
{
if(!notPrime[i])
{
prime[++cnt] = from[i] = i;
num[i] = 1;
}
for(int j = 1; prime[j] * i <= n && j <= cnt; j++)
{
from[i * prime[j]] = prime[j];
num[i * prime[j]] = num[i] + 1;
notPrime[i * prime[j]] = 1;
if(i % prime[j] == 0) break;
}
}
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
scanf("%d", &t);
sieve(1e6 + 3);
while(t--)
{
scanf("%lld%lld", &n, &c);
printf("%lld\n", qpow(c, num[n], mod));
}
return 0;
}
|
C.
题目描述：
题解：
代码：
题目描述：
给出一个数字字符串，要求分割为若干段，使得最大值和最小值的差尽量小
数据范围
$ 2 \le n \le 10^5,’0’ \le s[i] \le ‘9’,\sum{n}\le 10^6 $
题解：
显然，答案 $ \le 9 $ ，每一段都是一位数
下面分两种情况继续讨论：
- 划分的每一段长度都相等（枚举约数，线性扫一遍）
- 最大段和最小段长度相差 $ 1 $ ，形式只能是 $ 99\cdots9x $ 和 $ 100\cdots y $ ， $ x = 2\cdots9,y=0\cdots7 $ 是对应的。因为 $ x $ 不能是 $ 1 $ $ y $ 不能是 $ 9 $ ，容易发现，满足这种构型的
方案只有 $ O(1) $ 种，稍微特判一下即可。复杂度 $ 𝑶(𝑁) $
代码：
E.
题目描述：
题解：
代码：
题目描述：
两条线 $ AB,CD $ ，输入距离 $ AC,AD,BC,BD $ ，判断是下面那种情况
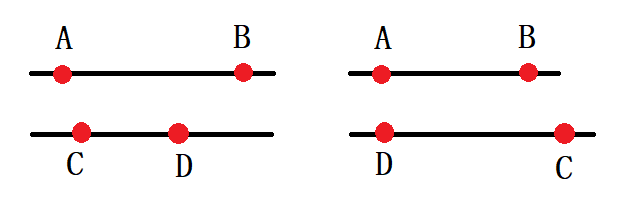
题解：
有很多种做法
- 可以找到最大值，如果最大值来自 AD 或 BC ，则 $ AB//CD $ ，否则 $ AB//DC $ 。
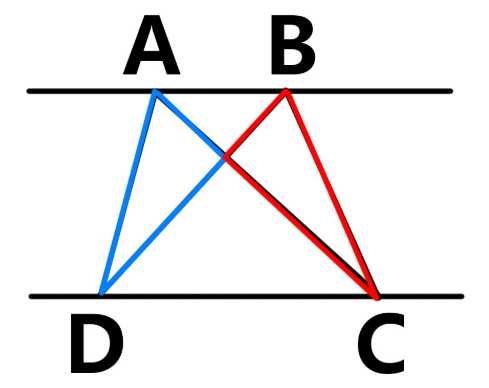也可以像这样，得到两个三角形，判断一下两边和大于第三边， $ AC+BD $ 和 $ AD+BC $
代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| #include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
const LL MOD = 1e9 + 9;
int t;
int a, b, c, d;
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
scanf("%d", &t);
while(t--)
{
scanf("%d%d%d%d", &a,&b,&c,&d);
cout << ((a+d < b+c) ? "AB//CD" : "AB//DC") << endl;
}
return 0;
}
|
G.
题目描述：
题解：
代码：
题目描述：
$ B $ 题的 $ hard $ 版本，给出 $ 1-n $ 的一个序列，求出两个长度最大为 $ m $ 的子集 $ A,B $ ，对应的元素有 $ gcd(a_i, b_i)>1 $
数据范围：
$ 4\le n \le 2\times10^5,\sum{n} \le 2 \times 10^5 $
题解：
构造，方法是
$ p\times2>n $ 的 $ p $ 必然不能匹配，将它们除去。
倒序枚举所有质因子 $ p $ ，考虑所有是 $ p $ 的倍数、且未被匹
配的数，任意将它们进行匹配。
如果个数是奇数就留下 $ p\times2 $ 。
最后把剩下的偶数都随意匹配一下。
代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 10;
const ll mod = 1e9 + 7;
int t;
ll n, c, d;
vector<pair<ll, ll> > ans;
ll a[maxn];
ll prime[maxn];
bool notPrime[maxn];
ll cnt = 0;
ll from[maxn];
void sieve(ll n)
{
for(ll i = 2; i <= n; i++)
{
if(!notPrime[i]) prime[++cnt] = from[i] = i;
for(ll j = 1; prime[j] * i <= n && j <= cnt; j++)
{
from[i * prime[j]] = prime[j];
notPrime[i * prime[j]] = 1;
if(i % prime[j] == 0) break;
}
}
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
scanf("%d", &t);
sieve(2e5 + 3);
while(t--)
{
scanf("%d", &n);
ans.clear();
memset(a, 0, sizeof(a));
ll p = 0;
for(ll i = 1; i <= cnt; i++)
{
if(prime[i] > n) break;
if(prime[i] > (n >> 1)) a[prime[i]] = -1, p = i;
}
int tmp, k = 0;
for(ll i = p; i >= 1; i--)
{
if(a[prime[i]] == -1) continue;
k = 0;
for(ll j = 1; j * prime[i] <= n; j++)
{
if(a[j * prime[i]] == -1 || j == 2) continue;
k++;
if(k&1) tmp = j * prime[i];
else
{
ans.push_back({tmp, j * prime[i]});
k = 0;
a[tmp] = a[j * prime[i]] = -1;
}
}
if(k == 1)
{
ans.push_back({tmp, 2 * prime[i]});
a[tmp] = a[2 * prime[i]] = -1;
}
}
k = 0;
for(ll i = 1; i <= n; i++)
{
if((i%2==0) && a[i] != -1)
{
k++;
if(k & 1) tmp = i;
else
{
ans.push_back({tmp, i});
k = 0;
}
}
}
printf("%d\n", ans.size());
for(auto x : ans)
{
printf("%lld %lld\n", x.first, x.second);
}
}
return 0;
}
|
I.
题目描述：
题解：
代码：