题目描述:
略
题解:
简单,略
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| #include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 2e6 + 10;
const int maxm = 8 + 5;
const ll mod = 998244353;
const int inf = 0x3f3f3f3f;
char s[maxn];
int t, n, m;
int a[maxn];
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
ios::sync_with_stdio(false);
cin.tie(0);
cin >> t;
int tot;
int ans;
while(t--)
{
cin >> n;
cin >> s;
tot = 0;
ans = 0;
for(int i = 0; i < n; i++)
{
if(s[i] == '2' || s[i] == '3')
{
ans++;
}
else if(s[i] == '1')
{
tot++;
}
else
{
if(tot > 0)
{
tot--;
ans++;
}
}
}
ans += tot / 2;
cout << ans << endl;
}
return 0;
}
|
题目描述:
略
题解:
简单。大意了,交了两发超时,果然是 $ cout $ 超时,换成 $ printf $ 就好了
直接记录转移的个数,记得直接模除转正。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| #include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 2e6 + 10;
const int maxm = 8 + 5;
const ll mod = 998244353;
const int inf = 0x3f3f3f3f;
char s[maxn];
int q;
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
ios::sync_with_stdio(false);
cin.tie(0);
cin >> s;
cin >> q;
char op;
int off;
int sum = 0;
int len = strlen(s);
while(q--)
{
cin >> op >> off;
if(op == 'A')
{
off--;
off = ((off + sum) % len + len) % len;
printf("%c\n", s[off]);
}
else
{
sum = sum + off;
sum = (sum % len + len) % len;
}
}
return 0;
}
|
题目描述:
给出 $ 20 $ 个点,判断是左手还是右手。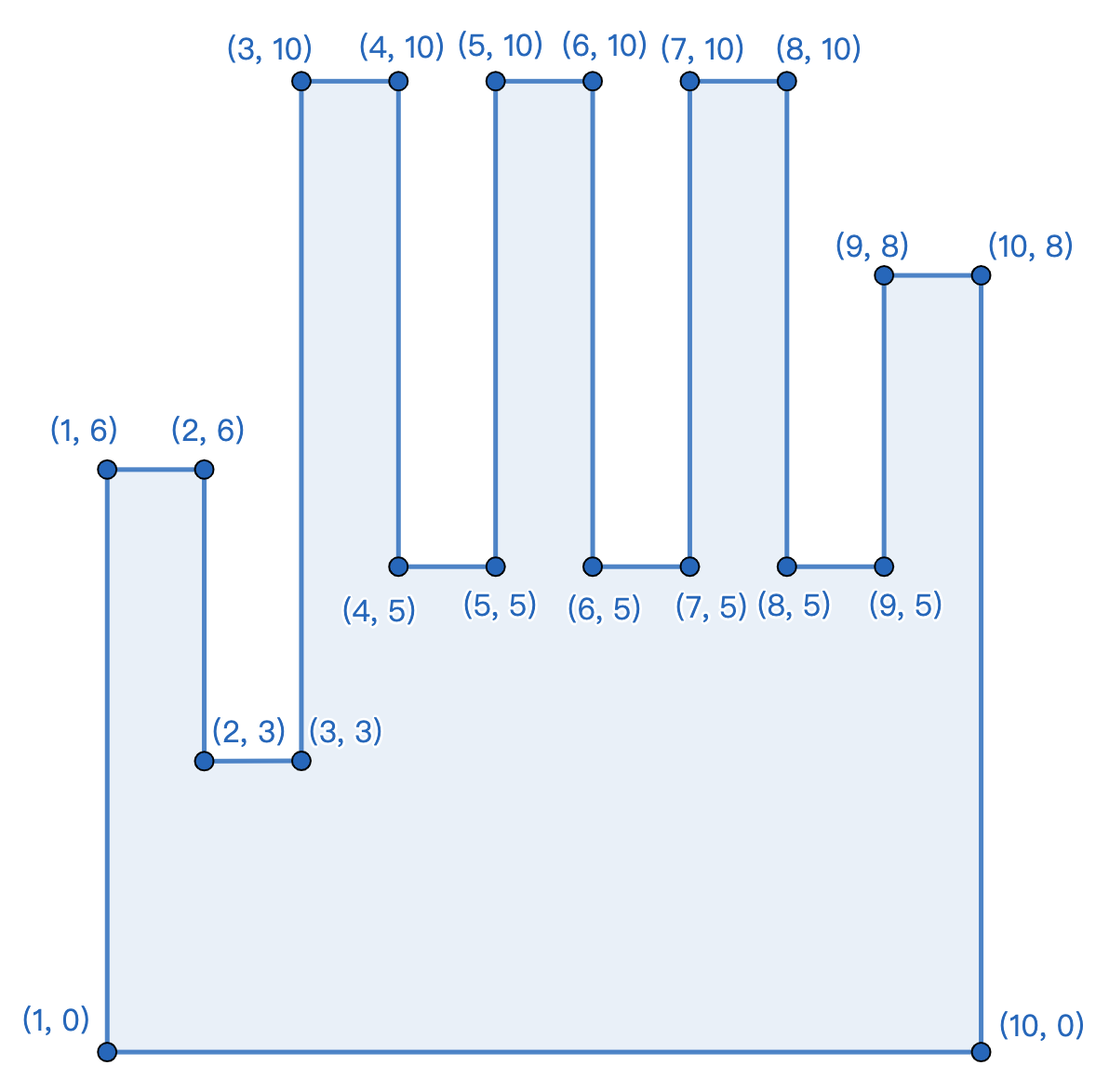
题解:
简单。首先根据边长判断,找到最长的边 $ 9 $ ,然后判断下一条边长度和方向。(用叉积就行)
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 40 + 10;
const int maxm = 8 + 5;
const ll mod = 998244353;
const int inf = 0x3f3f3f3f;
const double eqs = 1e-5;
char s[maxn];
int t, n, m;
int a[maxn];
struct Point
{
double x, y;
};
double CrossPro(Point x, Point y, Point z)
{
return (y.x - x.x) * (z.y - x.y) - (z.x - x.x) * (y.y - x.y);
}
double dis(Point x, Point y)
{
return sqrt((x.x - y.x) * (x.x - y.x) + (x.y - y.y) * (x.y - y.y));
}
Point point[maxn];
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
ios::sync_with_stdio(false);
cin.tie(0);
cin >> t;
bool flag;
while(t--)
{
flag = 0;
for(int i = 0; i < 20; i++)
{
cin >> point[i].x >> point[i].y;
}
for(int i = 0; i < 20; i++)
{
if(fabs(dis(point[i], point[(i + 1) % 20]) - 9) < eqs)
{
double dist = dis(point[(i + 1) % 20], point[(i + 2) % 20]);
if(fabs(dist - 6) < eqs)
{
if(CrossPro(point[(i + 1) % 20], point[(i + 2) % 20], point[i]) < 0) flag = 1;
}
else if(fabs(dist - 8) < eqs)
{
if(CrossPro(point[(i + 1) % 20], point[(i + 2) % 20], point[i]) > 0) flag = 1;
}
}
}
if(flag) cout << "right" << endl;
else cout << "left" << endl;
}
return 0;
}
|
D.
题目描述:
题解:
代码:
题目描述:
给出一个序列 $ a_i $ ,找到两个个 $ 1 - n $ 的排列和下标 $ 1 - n $ 对应的匹配,满足这两个匹配完全不同,而且需要两两匹配的总差值最小。输出和
题解:
我沙雕了,一直在扣 $ \Delta{x_i} $ ,忘了表示成元素差值的形式了,表示成差值形式的话很容易就发现是 $ dp $ 了。(;д;)
很容易发现长度 $ 4 $ 和 $ 6 $ 是最基本的单元,其他长度的都可以由他们组成。因为 $ n $ 是偶数,所以 $ n \pmod {4} = 0 || 2 $
首先对元素排序,假设排序后为
$ 1, 2, 3, 4 $ (此处数字只代表升序的数字,并无具体数值)
最小值为 $ (2-1)+(4-3) $
次小值为 $ (3-1) + (4-2) $ 或 $ (4-1)+(3-2) $
加在一起的话就变成了 $ 2\times(4-1) $ ,显然这就是规律,这也解释了为什么出题人让求两种不同的序列。
同理可以得到长度为 $ 6 $ 的情况 : $ 2\times(6-1) $
由此可以得到
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| #include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 2e5 + 10;
const int maxm = 8 + 5;
const ll mod = 998244353;
const int inf = 0x3f3f3f3f;
int t, n;
ll a[maxn];
ll dp[maxn];
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
ios::sync_with_stdio(false);
cin.tie(0);
cin >> t;
while(t--)
{
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
dp[i] = inf;
}
sort(a + 1, a + 1 + n);
dp[4] = a[4] - a[1];
dp[6] = a[6] - a[1];
for(int i = 8; i <= n; i += 2)
{
dp[i] = min(dp[i-4] + a[i] - a[i-3], dp[i-6] + a[i] - a[i - 5]);
}
cout << dp[n] * 2 << endl;
}
return 0;
}
|
题目描述:
给出 $ a, b $ ,构造分式
数据范围:
$ b\le2\times10^{6} $ , $ 1\le c $ , $ e\le4\times10^{12} $
注意一下范围,需要开 $ long\ long $
题解:
首先求 $ gcd(a, b) $ ,如果不互质的话,肯定可以直接构造,很简单
互质的话,需要判断质因数的个数,个数小于等于 $ 1 $ 的话,设 $ b = p^k $ , $ p_1 + p_2 = k $ , $ d = p^{p_1}, f = p^{p_2} $ ,则 $ \frac{c}{d} - \frac{e}{f} $ 得到的分数最简形式分母应为 $ p^{\max(p_1, p_2)} \le p^k $ ,而且右侧也是最简的,所以错误,无解。
大于 $ 1 $ 的话,肯定可以找到 $ d\times f = b $ ,然后对分子进行扩展欧几里得,假设 $ b = p_1^{k_1} \times p_2^{k_2}\times\cdots \times p_n^{k_n} $ ,可以构造 $ d = p_1^{k_1}, f = b / d $ ,这样的话 $ gcd(d, f) = 1 $ ,因此 $ cf - ed = gcd(d, f) = 1 $ ,可以用 $ exgcd() $ 求出来 $ c_1, e_1 $ ,然后两边同时乘以 $ a $ ,得到结果。
注意先用线性筛快速分解质因数
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
| #include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 2e6 + 10;
const int maxm = 8 + 5;
const ll mod = 998244353;
const int inf = 0x3f3f3f3f;
const double eqs = 1e-5;
ll a, b, c, d, e, f;
int t;
int prime[maxn], cnt = 0;
bool notPrime[maxn];
int from[maxn];
void sieve(int n)
{
for(int i = 2; i <= n; i++)
{
if(!notPrime[i]) prime[++cnt] = from[i] = i;
for(int j = 1; prime[j] * i <= n && j <= cnt; j++)
{
from[i * prime[j]] = prime[j];
notPrime[i * prime[j]] = 1;
if(i % prime[j] == 0) break;
}
}
}
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll exgcd(ll a, ll b, ll &x, ll &y)
{
if(b == 0)
{
x = 1, y = 0;
return a;
}
ll gcd = exgcd(b, a % b, y, x);
y -= a / b * x;
return gcd;
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
sieve(2e6 + 3);
scanf("%d", &t);
while(t--)
{
scanf("%lld %lld", &a, &b);
ll g = gcd(a, b);
if(g != 1)
{
a /= g;
b /= g;
printf("%lld %lld %lld %lld\n", a + 1, b, 1ll, b);
}
else
{
ll tmp = b;
while(from[b] > 1 && tmp % from[b] == 0) tmp /= from[b];
if(tmp == 1) {printf("-1 -1 -1 -1\n"); continue;}
d = 1, f = b;
while(f % from[b] == 0)
{
f /= from[b];
d *= from[b];
}
exgcd(f, d, c, e);
e = -e;
while(c <= 0 || e <= 0)
{
c += d;
e += f;
}
printf("%lld %lld %lld %lld\n", c * a, d, e * a, f);
}
}
return 0;
}
|
G.
题目描述:
题解:
代码:
