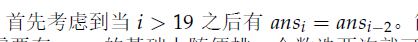Luobuyu's Blog

0%

nowcoder多校(第二场)

发表于 分类于 ， 热度： ℃ 评论：
本文字数： 14k 阅读时长 ≈ 13 分钟
2020年nowcoder暑期多校训练(第二场)，本场的题目还能够补得动。

A. All with Pairs

题目描述：

给出了 $ n $ 个字符串， $ s_1, s_2,\cdots,s_n $

定义 $ f(s, t) $ 等于前缀和后缀最长相等的部分

计算

$ 1 \le n \le 10^5 $ $ 1 \le |s_i|,\sum|s_i|\le10^6 $

题解：

数据范围比较大，直接暴力枚举的话肯定会超时。

题解中，每个字符串的前缀和后缀的总数量都是一样的 $ O(\sum|s_i|) $ ，所以可以对所有的字符串后缀 $ hash $ ，使用 $ map $ 记录，枚举每一个串的前缀，计算与之相同的后缀数。

但是会出现重复的，例如 $ aba $ ，会有两个前缀 $ a $ , $ aba $ 被计算到

如何去重？非常像 $ kmp $ 中的 $ next $ 数组，快速找到之前的比较短的匹配串。使用 $ cnt[nex[j]] -= cnt[j]; $ 去重，然后直接计算一下答案即可。

注意 $ base $ 的选取。之前选 $ 131 $ 直接 $ TLE $ 了

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int maxn = 1e6 + 10;
const int maxm = 1e5 + 10;
const ll mod = 998244353;
const int inf = 0x3f3f3f3f;
const int base = 233;

map<ull, int> mp;
int n;
string s[maxm];
int cnt[maxn];
void strHash(string s)
{
    ull p = 1, sum = 0;
    for(int i = s.length() - 1; i >= 0; i--)
    {
        sum += (s[i] - 'a' + 1) * p;
        p *= base;
        mp[sum]++;
    }
}
int nex[maxn];
void getNext(string s)
{
    int i = 0, t = -1;
    nex[0] = -1;
    while(i < s.length())
    {
        if(t == -1 || s[i] == s[t])
        {
            i++; t++;
            nex[i] = t;
        }
        else
        {
            t = nex[t];
        }
    }
}

ull getHash(string s, int j)
{
    ull sum = 0;
    for(int i = 0; i < j; i++)
    {
        sum = sum * base + (s[i] - 'a' + 1);
    }
    return sum;
}

int main()
{
#ifndef ONLINE_JUDGE
//    freopen("1.in", "r", stdin);
    freopen("in.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
#endif // debug
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n;
    ll ans = 0;
    for(int i = 1; i <= n; i++)
    {
        cin >> s[i];
        strHash(s[i]);
    }
    for(int i = 1; i <= n; i++)
    {
        // 枚举所有的前缀
        int len = s[i].length();
        ull sum = 0;
        for(int j = 1; j <= len; j++)
        {
            sum = sum * base + (s[i][j - 1] - 'a' + 1);
            cnt[j] = mp[sum];
        }
        getNext(s[i]);
        // 去重
        for(int j = 1; j <= len; j++)
        {
            if(nex[j] >= 0) cnt[nex[j]] -= cnt[j];
        }
        for(int j = 1; j <= len; j++)
        {
            ans += cnt[j]%mod*j%mod*j%mod;
            ans%=mod;
        }
    }
    cout << ans << endl;
    return 0;
}

B. Boundary

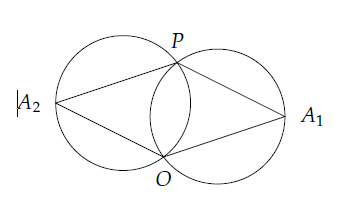
题目描述：

$ n $ 个点，需要找到一个圆，经过原点，且圆上点的个数最多

题解：

这个题精度卡的比较狠，使用分数类比较好

第一种方法，由于三点确定一个圆，经过了原点，所以只需要枚举另外两个点即可。手推一下圆心坐标公式就行了。注意需要使用 $ map $ 统计

第二种就是题解上的方法，使用 同弧所对的圆周角相等 这一性质，计算出来圆周角的大小，注意一些反向的情况即可，需要满足 $ \vec{OP} \times \vec{OA} < 0 $

2Txw6JGHgfcXVRl.png

代码：

第一种

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#pragma GCC optimize(3)
#include <cmath>
#include <vector>
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn = 2e3+55;
const double eps = 1e-7;
struct Point{double x,y;};
bool cmp(Point x,Point y){if(eps>fabs(x.x-y.x))return x.y<y.y;return x.x<y.x;}
struct node{ll a,b;ll aa,bb;}nn[maxn];
vector<Point>v;
int main(){
    int n;
    int maxxx=0;
    scanf("%d",&n);
    if(n==1){printf("1\n");return 0;}
    for(int i=0;i<n;++i){
        v.clear();
        scanf("%lld%lld",&nn[i].a,&nn[i].b);
        nn[i].aa=nn[i].a*nn[i].a;
        nn[i].bb=nn[i].b*nn[i].b;
        for(int j=0;j<i;++j){
            if(nn[i].b*nn[j].a==nn[j].b*nn[i].a)continue;
            ll yx=nn[j].a*(nn[i].aa+nn[i].bb)-nn[i].a*(nn[j].aa+nn[j].bb);
            ll yy=(ll)2*(nn[i].b*nn[j].a-nn[j].b*nn[i].a);
            ll xx=nn[j].b*(nn[i].aa+nn[i].bb)-nn[i].b*(nn[j].aa+nn[j].bb);
            ll xy=-yy;
            v.push_back({(double)xx/xy,(double)yx/yy});
        }
        int maxx=0,ans=1;
        sort(v.begin(),v.end(),cmp);
        for(int j=1;j<(int)v.size();++j){
            if(fabs(v[j].y-v[j-1].y)<eps&&fabs(v[j].x-v[j-1].x)<eps)ans++;
            else ans=1;
            maxx=max(maxx,ans);
        }
        maxxx=max(maxxx,maxx+1);
    }
    printf("%d\n",maxxx);
    return 0;
}

第二种（这里是给的标程）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef __int128_t LLL;
#define N 2000 + 5

int n, ans = 1, X[N], Y[N];

struct Frac
{
	LL fz, fm;
	Frac() : Frac(0, 1){}
	Frac(LL fz, LL fm) : fz(fz), fm(fm) {}
	bool operator < (const Frac &rhs)
	{
		return (LLL) fz * rhs.fm < (LLL) fm * rhs.fz;
	}
	bool operator == (const Frac &rhs)
	{
		return (LLL) fz * rhs.fm == (LLL) fm * rhs.fz;
	}
}A[N];

int Cross(int lhs, int rhs)
{
	return X[lhs] * Y[rhs] - X[rhs] * Y[lhs];
}

int Dot(int lhs, int rhs)
{
	return X[lhs] * X[rhs] + Y[lhs] * Y[rhs];
}

int Dis2(int lhs, int rhs)
{
	int dx = X[lhs] - X[rhs], dy = Y[lhs] - Y[rhs];
	return dx * dx + dy * dy;
}

int Sgn(int x)
{
	if (x > 0) return 1;
	if (x < 0) return -1;
	return 0;
}

Frac GetCosAngle2(int i, int j)
{
	int a2 = Dis2(0, i), b2 = Dis2(i, j), c2 = Dis2(0, j);
	int sgn = Sgn(b2 + c2 - a2);
	return Frac(1LL * sgn * (b2 + c2 - a2) * (b2 + c2 - a2), 4LL * b2 * c2);
}

int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; i ++)
		scanf("%d%d", X + i, Y + i);
	for (int i = 1; i <= n; i ++)
	{
		int cnt = 0;
		for (int j = 1; j <= n; j ++)
			if (Cross(i, j) > 0)
				A[++ cnt] = GetCosAngle2(i, j);
		sort(A + 1, A + cnt + 1);
		for (int l = 1, r; l <= cnt; l = r)
		{
			for (r = l; A[l] == A[r] && r <= cnt; r ++) ;
			ans = max(ans, r - l + 1);
		}
	}
	printf("%d\n", ans);
	return 0;
}

C. Cover the Tree

题目描述：

给出一棵无根树，找出可以覆盖树上所有边的最小的链数，以及每条链的开始和结尾编号

输入： $ n, 1\le n \le 2\times10^5 $ ， $ u, v $

输出：最少的链数，起点 终点

题解：

显然起点和终点全部选择叶子结点覆盖的边数最多，假设叶子结点有 $ s $ 个，所以链数最少为 $ n/2 $ 向上取整，难点在于如何构造出起点和终点。

题解做法：任意选择一个非叶子结点作为根，然后求 $ dfs $ 序，将所有的叶子结点按 $ dfs $ 序排序，假设 $ s $ 为偶数，那么所构造的 $ s/2 $ 条链为 $ l_1 \rightarrow l_{s/2 + 1},l_2 \rightarrow l_{s/2 + 2},\cdots,l_{s/2} \rightarrow l_s $

证明：

izPywpYC7sUZnTa.png

如果 $ s $ 是奇数，为根节点再接一个叶子结点，按照上述构造之后删除这条边即可。

不太清楚怎么回事，我用出度判断的时候直接出错了

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int maxn = 2e5 + 10;
const int maxm = 1e5 + 10;
const ll mod = 998244353;
const int inf = 0x3f3f3f3f;
const int base = 233;

vector<int> g[maxn];
int n, root;
int outdeg[maxn];
int cnt;
int ans[maxn];
void dfs(int u, int fa)
{
    if(g[u].size() == 1)
    {
        ans[++cnt] = u;
        return;
    }
    for(int i = 0; i < g[u].size(); i++)
    {
        int v = g[u][i];
        if(v == fa) continue;
        dfs(v, u);
    }
}

int main()
{
#ifndef ONLINE_JUDGE
//    freopen("1.in", "r", stdin);
    freopen("in.txt", "r", stdin);
//    freopen("out.txt", "w", stdout);
#endif // debug
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin >> n;
    int u, v;
    cnt = 0;
    memset(outdeg, 0, sizeof(outdeg));
    for(int i = 1; i <= n - 1; i++)
    {
        cin >> u >> v;
        outdeg[u]++;
        g[u].push_back(v);
        g[v].push_back(u);
    }

    if(n == 2)
    {
        cout << 1 << endl << u << " " << v << endl;
        return 0;
    }

    for(int i = 1; i <= n; i++)
    {
        if(g[i].size() > 1)
        {
            root = i;
            dfs(i, -1);
            break;
        }
    }

    if(cnt & 1) ans[++cnt] = root;
    cout << cnt / 2 << endl;
    for(int i = 1; i <= cnt / 2; i++)
    {
        cout << ans[i] << " " << ans[i + cnt / 2] << endl;
    }
    return 0;
}

D. Duration

题目描述：

给出一天中的两个时刻，输出之间相差的秒数

题解：

无

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
#include <cstdio>
#include <cctype>
#include <algorithm>
#include <cstring>
 
using namespace std;
using longs = long long;
using uint = unsigned;
 
inline int nextInt()
{
    int x = 0, f = 1, ch = getchar();
    while (!isdigit(ch)) if (ch == '-') f = -1, ch = getchar();
    while (isdigit(ch)) x = x * 10 + ch - 48, ch = getchar();
    return x * f;
}
 
int main()
{
    auto h1 = nextInt(), m1 = nextInt(), s1 = nextInt();
    auto h2 = nextInt(), m2 = nextInt(), s2 = nextInt();
    auto $$ 1 = h1 * 3600 + m1 * 60 + s1;
    auto $$ 2 = h2 * 3600 + m2 * 60 + s2;
    cout << abs( $ 1 - $ 2);
 
    return 0;
}

E. Exclusive OR

题目描述：

给出一个序列，找到 $ i $ 个数，可以重复选择，计算连续异或的最大值

$ 0 \le a_i \le 2^{18}，1 \le n \le 2 * 10 ^5 $

题解：

根据线性基的知识容易推出 不超过 $ w=logM_x $ 个数字即可拼出最大值 其中 $ M_x $ 为值域. 因此选出 $ 18 $ 个数字就能得到最大值了。

UaWYNuCtHkjQpsF.png

只需要处理 $ i \le 19 $ 的所有答案即可， $ i \ge 20 $ 时， $ ans_i = ans_{i-2} $ 题解中给出了证明。异或运算具有可逆性。

计算异或需要使用 $ FWT $

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
#include <cstdio>
#include <algorithm>
using namespace std;
#define N 200000 + 5
#define LOGW 18
#define W (1 << LOGW)
#define Mod 998244353
#define Inv2 499122177

int n, A[N], T[W], CT[W], Ans[N];

inline int Inc(int u, int v)
{
	return u >= (Mod - v) ? u - (Mod - v) : u + v;
}

void FWT(int *p)
{
	for (int k = 1; k < W; k <<= 1)
		for (int i = 0; i < W; i ++)
			if ((i & k) == 0)
			{
				int u = Inc(p[i], p[i | k]);
				int v = Inc(p[i], Mod - p[i | k]);
				p[i] = u, p[i | k] = v;
			}
}

void NFWT(int *p)
{
	for (int k = W / 2; k; k >>= 1)
		for (int i = 0; i < W; i ++)
			if ((i & k) == 0)
			{
				int u = 1LL * Inc(p[i], p[i | k]) * Inv2 % Mod;
				int v = 1LL * Inc(p[i], Mod - p[i | k]) * Inv2 % Mod;
				p[i] = u, p[i | k] = v;
			}
}

int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; i ++)
		scanf("%d", A + i);
	CT[0] = 1;
	for (int i = 1; i <= n; i ++)
		T[A[i]] = 1;
	FWT(CT), FWT(T);
	int lim = min(LOGW + 1, n);
	for (int i = 1; i <= lim; i ++)
	{
		for (int j = 0; j < W; j ++)
			CT[j] = 1LL * CT[j] * T[j] % Mod;
		NFWT(CT);
		int &mx = Ans[i];
		mx = -1;
		for (int j = W - 1; j >= 0 && (mx == -1); j --)
		{
			if (CT[j])
				mx = j;
			CT[j] = CT[j] ? 1 : 0;
		}
		FWT(CT);
	}
	for (int i = lim + 1; i <= n; i ++)
		Ans[i] = Ans[i - 2];
	for (int i = 1; i <= n; i ++)
		printf("%d%c", Ans[i], i == n ? '\n' : ' ');
	return 0;
}

#include<bits/stdc++.h>
using namespace std;
const int mod=998244353,r2=mod/2+1;
int a[300010],b[300010];
int ans[25];
int ad(int x,int y){
    return x+y>=mod?x+y-mod:x+y;
}
void fwtxor(int a[],int k,int arr){
    for(int mid=1;mid<k;mid<<=1){
        for(int i=0;i<k;i+=mid<<1){
            for(int j=0;j<mid;j++){
                int x=a[i+j],y=a[i+j+mid];
                a[i+j]=ad(x,y),a[i+j+mid]=ad(x,mod-y);
                if(arr==-1){
                    a[i+j]=(long long)a[i+j]*r2%mod;
                    a[i+j+mid]=(long long)a[i+j+mid]*r2%mod;
                }
            }
        }
    }
}
int main(){
    int n;
    scanf("%d",&n);
    int mx=0;
    for(int i=0;i<n;i++){
        int u;
        scanf("%d",&u);
        a[u]=1;
        mx=max(mx,u);
    }
    int k=1,l=0;
    while(k<=mx)k<<=1,l++;
    for(int i=0;i<=mx;i++)b[i]=a[i];
    fwtxor(a,k,1);
    for(int i=1;i<=l+2&&i<=n;i++){
        for(int j=k;j>=0;j--){
            if(b[j]){
                ans[i]=j;
                break;
            }
        }
        fwtxor(b,k,1);
        for(int i=0;i<k;i++)b[i]=(long long)a[i]*b[i]%mod;
        fwtxor(b,k,-1);
    }
    for(int i=1;i<=n;i++){
        if(i>l+2){
            if(i%2==l%2)printf("%d ",ans[l+2]);
            else printf("%d ",ans[l+1]);
        }
        else printf("%d ",ans[i]);
    }
}

F. Fake Maxpooling

题目描述：

给出一个 $ n * m $ 矩阵，求 $ k $ 子矩阵中最大值的和

题解：

维护区间最值，想到了单调队列，滑动窗口。直接每行，每列分别维护，得到新的矩阵。计算矩阵和即可

Gn4Kct8LiqYVBaQ.png

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 5e3 + 10;
const int maxm = 8 + 5;
const ll mod = 998244353;
const int inf = 0x3f3f3f3f;

int n, m, k;
int a[maxn][maxn];
int b[maxn][maxn];
int q[maxn];
int gcd(int a, int b)
{
    if(b == 0) return a;
    return gcd(b, a % b);
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif // debug
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n >> m >> k;
    // 类似埃氏筛
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            if(!a[i][j]) 
                for(int k = 1; k * i <= n && k * j <= m; k++)
                {
                    a[k * i][k * j] = i * j * k;
                }
        }
    }

    int hh = 0, tt = -1;
    int t;
    for(int j = 0; j < m; j++)
    {
        t = 0;
        hh = 0, tt = -1;
        for(int i = 0; i < n; i++)
        {
            while(hh <= tt && i - k + 1 > q[hh]) hh++;
            while(hh <= tt && a[q[tt]][j] <= a[i][j]) tt--;
            q[++tt] = i;
            if(i >= k - 1) b[t++][j] = a[q[hh]][j];
        }
    }
    for(int i = 0; i < t; i++)
    {
        for(int j = 0; j < m; j++)
        {
            a[i][j] = b[i][j];
        }
    }

    int p = 0;
    for(int i = 0; i < t; i++)
    {
        p = 0;
        hh = 0, tt = -1;
        for(int j = 0; j < m; j++)
        {
            while(hh <= tt && j - k + 1 > q[hh]) hh++;
            while(hh <= tt && a[i][q[tt]] <= a[i][j]) tt--;
            q[++tt] = j;
            if(j >= k - 1) b[i][p++] = a[i][q[hh]];
        }
    }

    ll ans = 0;
    for(int i = 0; i < t; i++)
    {
        for(int j = 0; j < p; j++)
        {
            ans += b[i][j];
        }
    }
    cout << ans << endl;
    return 0;
}

G. Greater and Greater

题目描述：

给出两个数组 $ a $ ， $ b $ ，找出 $ a $ 有多少个子序列，满足 $ a_i >= b_i $

题解：

之前想的是魔改 $ kmp $ ，结果样例之类的过了，但是交上去 $ wa $ 了。

看了题解是需要使用 $ bitset $ ，注意 $ bitset $ 的用法，移位操作比较特殊

首先进行排序操作，然后对 $ a $ 的从大到小，对 $ b $ 进行检测，满足后需要进行移位操作，因为需要满足最后的子序列长度为 $ m $ ，所以向右移位（实际是向左移位的）看看所需长度的序列是否满足（与运算即可）

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 2e5 + 10;
const int maxm = 8 + 5;
const ll mod = 998244353;
const int inf = 0x3f3f3f3f;
int n, m, k;
vector<pair<int, int> > a, b;
bitset<maxn> ans, g;
int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif // debug
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n >> m;
    int x;
    for(int i = 1; i <= n; i++)
    {
        cin >> x;
        a.push_back({x, i});
    }
    for(int i = 1; i <= m; i++)
    {
        cin >> x;
        b.push_back({x, i});
    }

    sort(a.begin(), a.end());
    sort(b.begin(), b.end());
    ans.set();
    for(int i = m - 1, j = n - 1; i >= 0; i--)
    {
        while(j >= 0 && a[j].first >= b[i].first)
        {
            g.set(a[j--].second);
        }
        ans &= g >> b[i].second;
    }
    cout << ans.count() << endl;
    return 0;
}

G.

题目描述：

题解：

代码：

1
2


H.

题目描述：

题解：

代码：

1
2


I.

题目描述：

题解：

代码：

1
2


J. Just Shuffle

题目描述：

给出一个排列 $ B $ ，找到一种置换方法 $ P $ ，使得自然数序列在执行 $ k $ 次之后可以得到 $ B $ ， $ A^k = B $ ， $ k $ 是一个大质数。

题解：

等式两边同时 $ t $ 次幂，得到 $ A^{k\times t} = B^t $ ，当 $ t = inv(k) $ 时，可以得到 $ B^t = A $ ，所以很简单，直接求一下 $ B $ 的 $ t $ 次幂即可

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e5 + 10;
int n, k;
int a[maxn];
int st[maxn], top;
int ans[maxn];
bool vis[maxn];
int tmp[maxn];
int exgcd(int a, int b, int &x, int &y)
{
    if (b == 0)
    {
        x = 1, y = 0;
        return a;
    }
    int x1, y1, gcd;
    gcd = exgcd(b, a % b, x1, y1);
    x = y1, y = x1 - a / b * y1;
    return gcd;
}

int getinv(int a, int b)
{
    int x, y;
    exgcd(a, b, x, y);
    x %= b;
    if(x < 0)
        x += b;
    return x;
}
void getCycle(int x)
{
    top = 0;
    do
    {
        vis[x] = true;
        st[++top] = x;
        x = a[x];
    } while (!vis[x]);
    
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
    }
    for (int i = 1; i <= n; i++)
    {
        if(!vis[i])
        {
            getCycle(i);
            int inv = getinv(k, top);
            for (int j = 1, p = 1; j <= top; j++)
            {
                tmp[j] = st[p];
                p = (p + inv - 1) % top + 1;
            }
            tmp[top + 1] = tmp[1];
            for (int j = 1; j <= top; j++)
            {
                ans[tmp[j]] = tmp[j + 1];
            }
        }
    }

    for (int i = 1; i <= n; i++)
    {
        printf("%d ", ans[i]);
    }
    return 0;
}

K. Keyboard Free

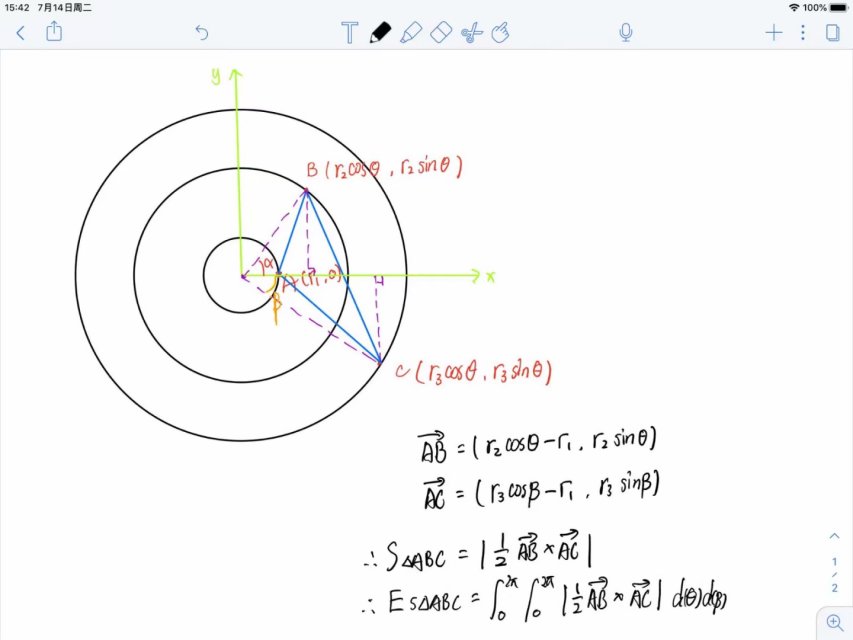
题目描述：

三个同心圆，每个圆上有一个点，求组成三角形面积的期望

题解：

需要求期望，只需要把面积表示的公式求出来，然后积分应该就行了。

6PO5CaXIvisFRS3.jpg

在利用向量表示出三角形的面积后，会带有两个以角度为变量的参数，且积分时带有绝对值，因为题目对精度的要求不高，所以我们可以将角度做等分。

http://www.koule2333.top:3000/s/HJn9liYyw

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
using namespace std;
const double pi=acos(-1);
const int t=399;
int T;
double r[4],si[1010],co[1010];
void solve()
{
	scanf("%lf%lf%lf",&r[1],&r[2],&r[3]);
	sort(r+1,r+4); double ans=0;
	for (register int i=0;i<t;++i)
	 for (register int j=0;j<t;++j)
	  ans+=abs((r[3]*co[j]-r[1])*r[2]*si[i]-(r[2]*co[i]-r[1])*r[3]*si[j]);
	printf("%.1f\n",ans/2./(double)t/(double)t);
}
int main()
{
	double a=0,v=2.*pi/(double)t;
	for (int i=0;i<=t;i++,a+=v) si[i]=sin(a),co[i]=cos(a);
	scanf("%d",&T);
	while (T--) solve();
return 0;
}