Luobuyu's Blog

0%

hdu多校(第八场)

发表于 分类于 ， 热度： ℃ 评论：
本文字数： 14k 阅读时长 ≈ 13 分钟
2020年hdu暑期多校训练(第八场)，题目还行，就是做题老是遗漏点东西，导致做的比较慢。涉及一些没学过的知识，加紧学习。

A.

题目描述：

数据范围：

题解：

代码：

1
2


B.

题目描述：

数据范围：

题解：

代码：

1
2


C. Clockwise or Counterclockwise

题目描述：

圆心在 $ O(0,0) $ 的一个圆，给出圆上三个点 $ A,B,C $ ，问 $ A\to B\to C $ 是顺时针还是逆时针。

数据范围：
$ 1\le T \le 1000 $

题解：

用向量叉积即可 $ \vec{AB} \times \vec{BC} \gt 0 $ 表明 $ C $ 在 $ AB $ 的右侧，逆时针

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <bits/stdc++.h>
#define ll long long
namespace FAST_IO
{
    template <class T>
    inline void read(T &x)
    {
        T flag = 1;
        x = 0;
        char ch = getchar();
        while (ch < '0' || ch > '9')
        {
            if (ch == '-')
                flag = -1;
            ch = getchar();
        }
        while (ch >= '0' && ch <= '9')
        {
            x = (x << 3) + (x << 1) + (ch ^ 48), ch = getchar();
        }
        x *= flag;
    }

    template <class T, class... _T>
    inline void read(T &x, _T &... y)
    {
        return read(x), read(y...);
    }

} // namespace FAST_IO
using namespace std;
using namespace FAST_IO;
const ll mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF_LL = 0x3f3f3f3f3f3f3f3f;
const double eqs = 1e-5;
const int maxn = 1e3 + 10;
const int maxm = 1e5 + 10;
int t, n, m, k;
ll x_1, y_1, x2, y2, x3, y3;
int main()
{
// #define COMP_DATA
#ifndef ONLINE_JUDGE
#ifdef COMP_DATA
    freopen("/mnt/f/文档/课件/ACM比赛/2020hdu多校/第四场/data/E.in", "r", stdin);
    freopen("out.txt", "w", stdout);
#else
    freopen("in.txt", "r", stdin);
#endif
#endif

    int tcase;
    read(tcase);
    while (tcase--)
    {
        read(x_1, y_1, x2, y2, x3, y3);
        if(((x2 - x_1) * (y3 - y2) - (x3 - x2) * (y2 - y_1)) > 0)
        {
            printf("Counterclockwise\n");
        }
        else
        {
            printf("Clockwise\n");
        }
    }
    return 0;
}

D. Discovery of Cycles

题目描述：

现在有一张 $ n $ 个点 $ m $ 条边的连通图，有 $ q $ 个询问，每次问你区间 $ l~r $ 的边是否能组成一个及以上的简单环。

数据范围：
$ 1\le T \le 10 \\ 1\le n,m,q \le 3 \times 10^5 $

题解：

使用到了 $ LCT $ 题解还是挺详细的，不过 $ LCT $ 还没学过

我们可以给每一条边 $ i $ 求出以这条边作为左端点, 在最短的区间内能形成环的最小右端点, 标记为 $ R_i $ , 如果不存在这样的右端点（即从当前到结尾所有边都不能组成环）, 则让 $ R_i = m + 1 $ , 显然暴力求这个 $ R_i $ 是不允许的.

显然 $ R_i $ 一定是递增的, 所以如果我们可以快速删边的话, 那么这个就能快速的求解了．于是就考虑到可以用 $ LCT $ 来优化这个过程, 即只需要维护左端点和右端点, 肯定会尽量拓展右端点, 拓展不了就删掉左端点所在的边然后移动左端点．不断重复这个过程就可以求解所有的 $ R_i $ 了．

时间复杂度 $ O(mlog n + q) $ ．

代码：

这里先放上题解代码，等学会后再搞

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
#include <bits/stdc++.h>
using namespace std;
#define N 300000 + 5

int n, m, q, E[N][2], Max[N], Stack[N];

struct Node
{
    int l, r, fa, pre;
    bool flag;
}h[N];

void init()
{
    memset(h,0,sizeof(h));
    memset(E,0,sizeof(E));
    memset(Max,0,sizeof(Max));
    memset(Stack,0,sizeof(Stack));
}

inline void swap(int &u, int &v)
{
    u = u + v, v = u - v, u = u - v;
}

inline void zig(int x)
{
    int y = h[x].fa, z = h[y].fa;
    if (y == h[z].l) h[z].l = x;
    if (y == h[z].r) h[z].r = x;
    h[x].fa = z, h[y].fa = x;
    h[y].l = h[x].r, h[h[x].r].fa = y, h[x].r = y;
}

inline void zag(int x)
{
    int y = h[x].fa, z = h[y].fa;
    if (y == h[z].l) h[z].l = x;
    if (y == h[z].r) h[z].r = x;
    h[x].fa = z, h[y].fa = x;
    h[y].r = h[x].l, h[h[x].l].fa = y, h[x].l = y;
}

inline void push(int x)
{
    if (h[x].flag)
    {
        h[h[x].l].flag ^= 1;
        h[h[x].r].flag ^= 1;
        swap(h[x].l, h[x].r);
        h[x].flag = 0;
    }
}

inline void Splay(int x)
{
    int rt = x;
    for (; h[rt].fa; rt = h[rt].fa) Stack[++ Stack[0]] = rt;
    push(rt);
    while (Stack[0]) push(Stack[Stack[0] --]);
    if (rt == x) return ;
    h[x].pre = h[rt].pre;
    h[rt].pre = 0;
    while (h[x].fa)
    {
        int y = h[x].fa, z = h[y].fa;
        if (x == h[y].l)
        {
            if (y == h[z].l) zig(y);
            zig(x);
        }
        if (x == h[y].r)
        {
            if (y == h[z].r) zag(y);
            zag(x);
        }
    }
}

inline void Expose(int x)
{
    for (int y = 0; x; x = h[x].pre)
    {
        Splay(x);
        h[h[x].r].fa = 0;
        h[h[x].r].pre = x;
        h[x].r = y;
        h[y].fa = x;
        h[y].pre = 0;
        y = x;
    }
}

inline bool Connect(int u, int v)
{
    Expose(u);
    Splay(u);
    for (; h[v].fa || h[v].pre; v = h[v].fa ? h[v].fa : h[v].pre) ;
    return u == v;
}

inline void Make_Root(int x)
{
    Expose(x);
    Splay(x);
    h[x].flag ^= 1;
}

inline void Add(int u, int v)
{
    Make_Root(u);
    h[u].pre = v;
}

inline void Cut(int u, int v)
{
    Make_Root(u);
    Expose(v);
    Splay(v);
    h[h[v].l].fa = 0;
    h[v].l = 0;
}

int main()
{
    int T;scanf("%d",&T);
    while(T--)
    {
        init();
        scanf("%d%d%d", &n, &m, &q);
        for (int i = 1; i <= m; i ++)
            scanf("%d%d", E[i], E[i] + 1);
        int i = 1, t = 1;
        while (t <= m)
        {
            if (i <= m && !Connect(E[i][0], E[i][1]))
                Add(E[i][0], E[i][1]), i ++;
            else
            {
                Max[t] = i;
                Cut(E[t][0], E[t][1]);
                t ++;
            }
        }
        int last=0;
        while (q --)
        {
            int u, v;
            scanf("%d%d", &u, &v);
            u=(u^last)%m+1;
            v=(v^last)%m+1;
            if (u>v) swap(u,v);
            if (v >= Max[u]) last=1,puts("Yes");
            else last=0,puts("No");
        }
    }
    return 0;
}

E.

题目描述：

数据范围：

题解：

代码：

1
2


F. Fluctuation Limit

题目描述：

给出 $ n，k $ ， $ n $ 段区间，在区间中选出一些数满足 $ |a_i - a_{i+1}| \le k $

数据范围：
$ 1\le T \le 10^5 \\ 2\le n \le 10^5,0\le k \le 10^9\\ 0\le l_i \le r_i \le 10^9 $

题解：

题目也比较简单，但是一开始考虑的漏了。一开始只考虑了把左边区间的限制带到右边，然后直接输出边界即可。但是最后发现有问题。

1
2
3
4
5
1
3 1
1 10
0 15
10 12

这组样例直接卡掉。仍然需要限制。跑两遍即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF_LL = 0x3f3f3f3f3f3f3f3f;
const double eqs = 1e-5;
const int maxn = 1e5 + 10;
const int maxm = 1e5 + 10;
int read()
{
    int x = 0, flag = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
            flag = 1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        x = (x << 3) + (x << 1) + (ch ^ 48), ch = getchar();
    }
    if (flag)
        return -x;
    return x;
}
int t, n, m, k, p;

struct Node
{
    int l, r;
} node[maxn];
int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
    // freopen("out.txt", "w", stdout);
#endif

    int tcase = read();
    while (tcase--)
    {
        n = read(), k = read();
        bool flag = true;
        for (int i = 1; i <= n; i++)
        {
            node[i].l = read(), node[i].r = read();
        }
        for (int i = n - 1; i >= 1; i--)
        {
            node[i].r = min(node[i + 1].r + k, node[i].r);
            node[i].l = max(node[i + 1].l - k, node[i].l);
            if (node[i].l > node[i].r)
            {
                flag = false;
                break;
            }
        }
        if (flag)
        {
            for (int i = 2; i <= n; i++)
            {
                node[i].r = min(node[i - 1].r + k, node[i].r);
                node[i].l = max(node[i - 1].l - k, node[i].l);
                if (node[i].l > node[i].r)
                {
                    flag = false;
                    break;
                }
            }

            if (flag)
            {
                printf("YES\n");
                for (int i = 1; i <= n; i++)
                {
                    printf("%d%c", node[i].l, " \n"[i == n]);
                }
            }
            else
            {
                printf("NO\n");
            }
        }
        else
        {
            printf("NO\n");
            continue;
        }
    }
    return 0;
}

G.

题目描述：

数据范围：

题解：

代码：

1
2


H. Hexagon

题目描述：

找规律构造题。

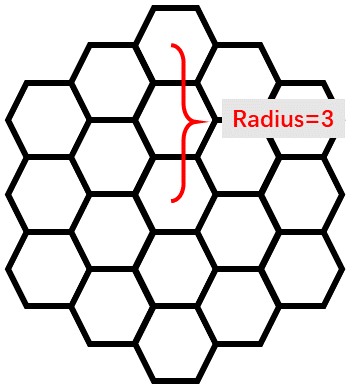
img111111111

img234

给出一个半径为 $ r $ 的蜂巢形图形。要求随意选择一个起点然后六个方向行走，后一步和前一步的方向尽可能不同，输出最大的不同的数量。

数据范围：
$ 1\le T \le 10^4 \\ 2\le n \le 500 \\ \sum n \le 2 \times10^4 $

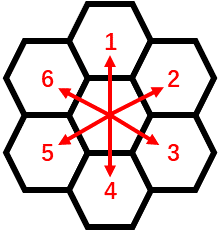
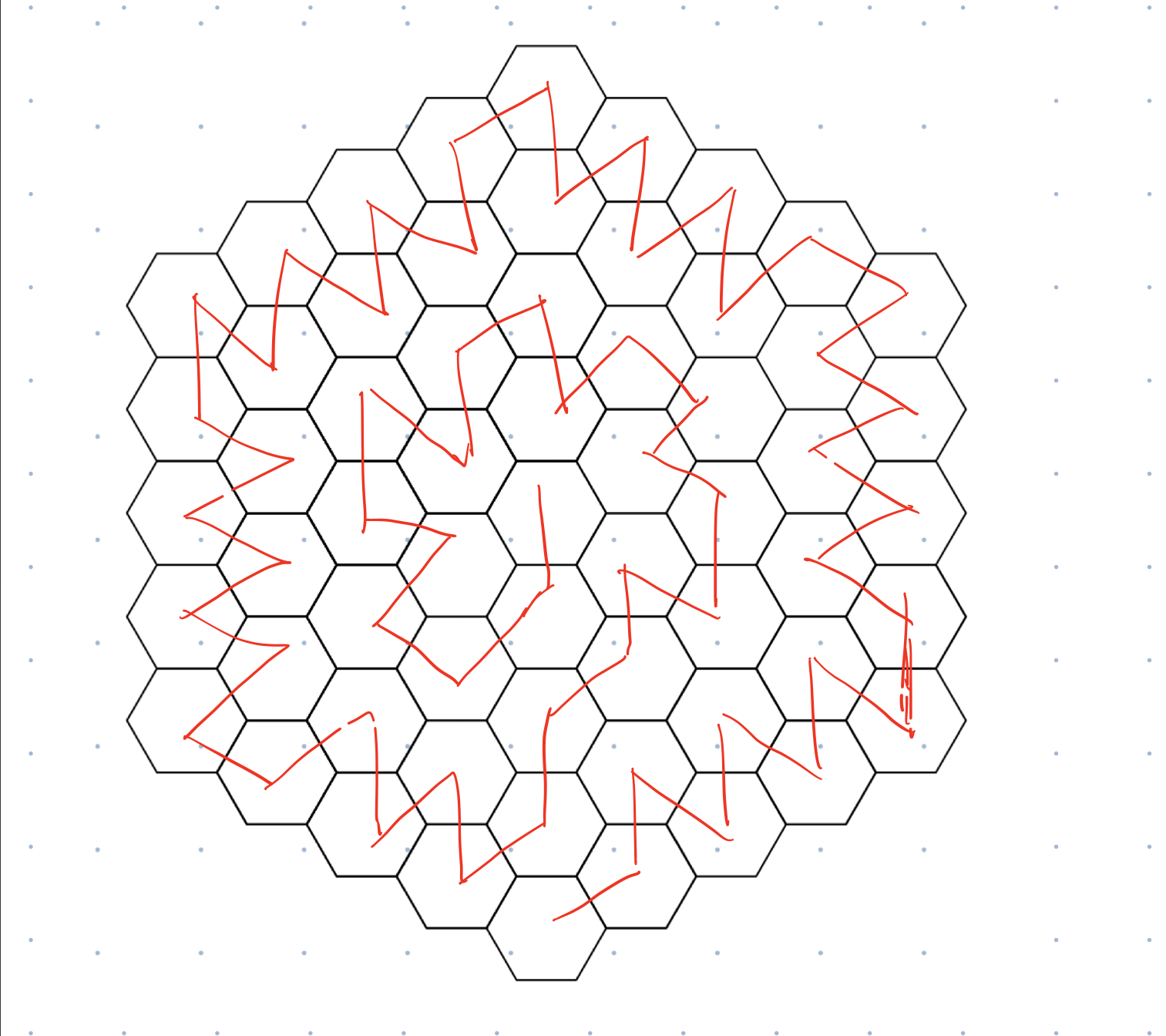
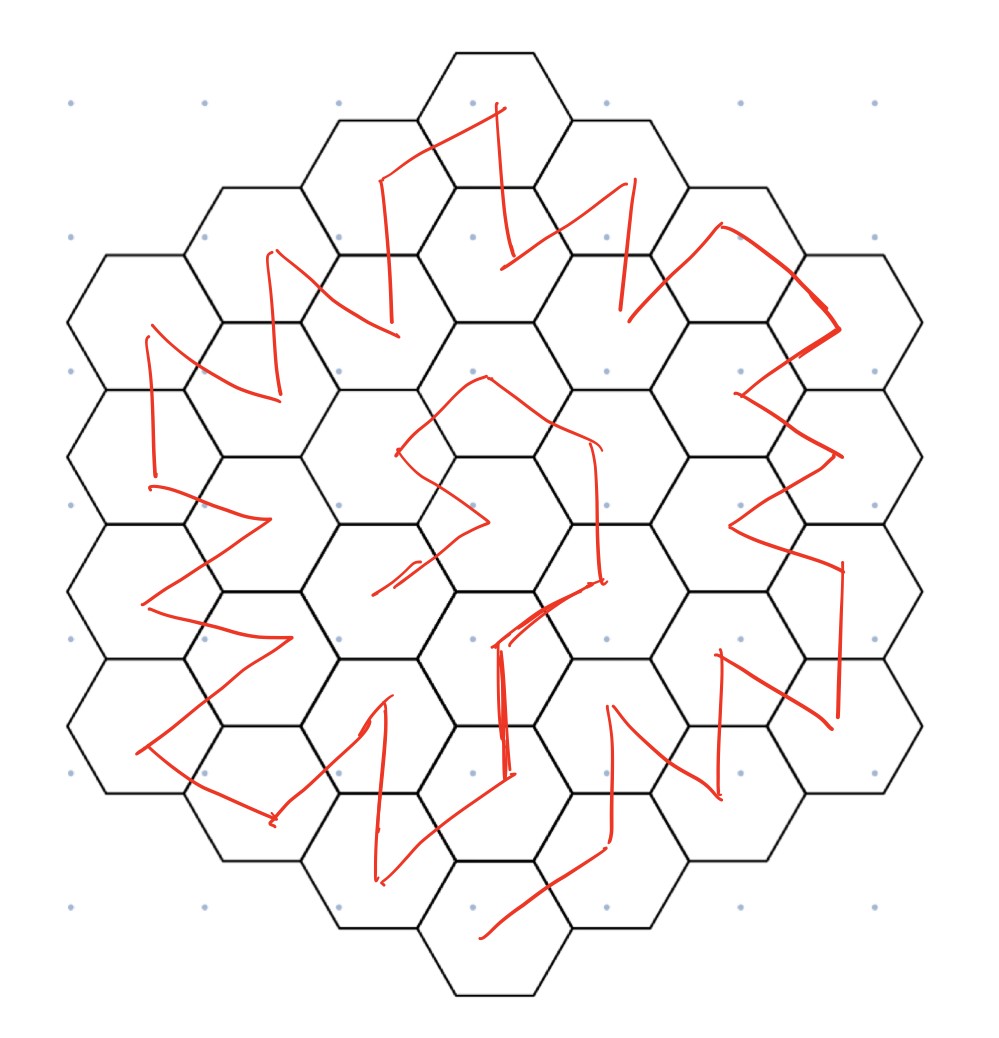
题解：

这个构造可以构造出满的，就是每一步和前一步的方向都是不同的。之前一直没有构造出来。最后发现构造不只有一种方法。构造肯定是从边缘起步把边缘走完然后就是进入内部，这里不同的方法可能不一样。只保留一个入口，把出口留在内部这样的发现可以递推。

2020-08-13 16.27.58

2020-08-13 16.29.04

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
#include <bits/stdc++.h>
#define ll long long
namespace FAST_IO
{
    template <class T>
    inline void read(T &x)
    {
        T flag = 1;
        x = 0;
        char ch = getchar();
        while (ch < '0' || ch > '9')
        {
            if (ch == '-')
                flag = -1;
            ch = getchar();
        }
        while (ch >= '0' && ch <= '9')
        {
            x = (x << 3) + (x << 1) + (ch ^ 48), ch = getchar();
        }
        x *= flag;
    }

    template <class T, class... _T>
    inline void read(T &x, _T &... y)
    {
        return read(x), read(y...);
    }

} // namespace FAST_IO
using namespace std;
using namespace FAST_IO;
const ll mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF_LL = 0x3f3f3f3f3f3f3f3f;
const double eqs = 1e-5;
const int maxn = 1e3 + 10;
const int maxm = 1e5 + 10;
int t, n, m, k;

char str[10][2][10] =
    {
        {"", ""},
        {"2", "13"},
        {"1", "62"},
        {"6", "51"},
        {"5", "46"},
        {"4", "35"},
        {"3", "24"}};

void edge(int index, int n)
{
    printf(str[index][0]);
    n -= 2;
    if(index == 6)
    {
        for(int i = 1; i <= n - 1; i++)
        {
            printf(str[index][1]);
        }
        printf("%c", str[index][1][0]);
        printf("1");
    }
    else
    {
        for(int i = 1; i <= n; i++)
        printf(str[index][1]);
    }
}
void solve(int n)
{
    if(n==2)
    {
        printf("216535");
        return;
    }
    if(n<2)
    {
        return;
    }
    for(int i = 1; i <= 6; i++)
        edge(i, n);
    solve(n - 2);
}

int main()
{
// #define COMP_DATA
#ifndef ONLINE_JUDGE
#ifdef COMP_DATA
    freopen("/mnt/f/文档/课件/ACM比赛/2020hdu多校/第四场/data/E.in", "r", stdin);
    freopen("out.txt", "w", stdout);
#else
    freopen("in.txt", "r", stdin);
#endif
#endif

    int tcase;
    read(tcase);
    while (tcase--)
    {
        read(n);
        solve(n);
        printf("\n");
    }
    return 0;
}

I. Isomorphic Strings

题目描述：

定义循环同构。给出一个字符串，分成 $ k $ 个字符串，每个字符串都是互相循环同构的。

数据范围：
$ 1\le T \le 1000\\1\le n \le 5 \times10^6 \\ k \gt1 \\ \sum n \le 2\times 10^7 $

题解：

题解中给的是 $ hash $ 做法，不过太慢了

image-20200814160916586

何佬的方法比较好。

首先记录一下各个字母的个数，然后求出 $ \gcd $ 为 $ m $ ，最后枚举 $ m $ 的约数就行。因为每一段同一个字母的个数肯定是一样的。判匹配使用 $ kmp $ ，他这个地方用的是第一节字符串为模式串，其他节的为主串，只需要求一次 $ next $ 数组就行了，还是比较快的。

我的 $ kmp $ 写的下标是从 $ 0 $ 开始的，因此传的时候传入字符串第一个字符首地址

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
#include <bits/stdc++.h>
#define ll long long
namespace FAST_IO
{
    template <class T>
    inline void read(T &x)
    {
        T flag = 1;
        x = 0;
        char ch = getchar();
        while (ch < '0' || ch > '9')
        {
            if (ch == '-')
                flag = -1;
            ch = getchar();
        }
        while (ch >= '0' && ch <= '9')
        {
            x = (x << 3) + (x << 1) + (ch ^ 48), ch = getchar();
        }
        x *= flag;
    }

    template <class T, class... _T>
    inline void read(T &x, _T &... y)
    {
        return read(x), read(y...);
    }

} // namespace FAST_IO
using namespace std;
using namespace FAST_IO;
const ll mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF_LL = 0x3f3f3f3f3f3f3f3f;
const double eqs = 1e-5;
const int maxn = 5e6 + 10;
const int maxm = 1e5 + 10;
int t, n, m, k;
char s[maxn];

int prime[maxn], cnt;
bool notPrime[maxn];
void sieve(int n)
{
    for (int i = 2; i <= n; i++)
    {
        if (!notPrime[maxn])
            prime[++cnt] = i, notPrime[i] = true;

        for (int j = 1; prime[j] * i <= n && j <= cnt; j++)
        {
            notPrime[i * prime[j]] = 1;
            if (i % prime[j] == 0)
                break;
        }
    }
}

int tot[30];

int nex[maxn];
void getNext(char *s, int l)
{
    nex[0] = -1;
    for (int t = -1, i = 0; i < l; nex[++i] = ++t)
        for (; ~t && s[i] != s[t]; t = nex[t])
            ;
}
int kmp(char *str, int l1, char *substr, int l2)
{
    int i = 0, j = 0;
    while (i < l1 && j < l2)
    {
        if (j == -1 || str[i] == substr[j])
            i++, j++;
        else
            j = nex[j];
    }
    if (j == l2)
        return i - j;
    return -1;
}
char str[maxn]; // 主串
bool check(int k)
{
    if (n % k)
        return false;
    int l = n / k;
    getNext(s + 1, l);
    for (int t = 1; t <= k - 1; t++)
    {
        for (int i = 1; i <= l; i++)
        {
            str[i] = str[i + l] = s[t * l + i];
        }
        if (kmp(str + 1, 2 * l - 1, s + 1, l) == -1)
        {
            return false;
        }
    }
    return true;
}

void init()
{
    memset(tot, 0, sizeof(tot));
}

int main()
{
// #define COMP_DATA
#ifndef ONLINE_JUDGE
#ifdef COMP_DATA
    freopen("/mnt/f/文档/课件/ACM比赛/2020hdu多校/第八场/发放/data/1009.in", "r", stdin);
    freopen("out.txt", "w", stdout);
#else
    freopen("in.txt", "r", stdin);
#endif
#endif

    int tcase;
    read(tcase);
    sieve(maxn - 5);
    while (tcase--)
    {
        read(n);
        scanf("%s", s + 1);
        if (n == 1)
        {
            printf("No\n");
            continue;
        }

        init();
        bool flag = false;
        for (int i = 1; i <= n; i++)
        {
            if (tot[s[i] - 'a' + 1]++ == 0)
            {
                tot[0]++;
            }
        }

        if (!notPrime[n]) // 素数
        {
            printf("%s\n", tot[0] == 1 ? "Yes" : "No");
        }
        else
        {
            if (tot[0] == 1)
            {
                printf("Yes\n");
                continue;
            }
            int m = -1;
            for (int i = 1; i <= 26; i++)
            {
                if (tot[i])
                {
                    if (m == -1)
                    {
                        m = tot[i];
                        continue;
                    }
                    m = __gcd(m, tot[i]);
                }
            }
            if (m == 1)
            {
                printf("No\n");
                continue;
            }
            if (m == n || check(m))
            {
                printf("Yes\n");
                continue;
            }

            for (int i = 2; i * i <= m; i++)
            {
                if (m % i == 0)
                {
                    if (check(i) || check(m / i))
                    {
                        printf("Yes\n");
                        flag = true;
                        break;
                    }
                }
            }
            if (!flag)
                printf("No\n");
        }
    }
    return 0;
}

J.

题目描述：

数据范围：

题解：

代码：

1
2


K. Kidnapper’s Matching Problem

题目描述：

给定 $ n,m,k(m≤n) $ ，给定长度为 $ n $ 的数组 $ a $ ，长度为 $ m $ 的数组 $ b $ ，长度为 $ k $ 的集合 $ S $ ，定义 $ 2^S_⊕ $ 为 $ S $ 的任意子集的异或和（xor_sum）的可能结果所形成的新集合，定义两等长集合 $ x, y $ 的 $ matches $ 函数，该函数会遍历判断 $ x_i \ xor\ y_i $ $ ∈ 2^S_⊕ $ ，如果对于所有的 $ i(i≤|x|,|y|) $ ， $ x_i\ xor\ y_i∈ 2^S_⊕xi $ 均成立，则 $ matches $ 返回 $ 1 $ ，否则返回 $ 0 $

问下式的值

数据范围：
$ 1\le T \le 2 \times 10^4 \\ 1\le n \le 2 \times10^5 \\ 1\le m \le min(n, 5 \times 10^4) \\\\ 1 \le k \le 100 \\ 0 \le a_i, b_i, S_i \le 2^{30} \\\\ \sum n \le 12 \times 10^5 ,\sum m \le 3 \times 10^ 5 , \sum k\le 6 \times 10^5 $

题解：

首先求出 $ S $ 的线性基 $ B $

image-20200814165100167

让 $ a $ 和 $ b $ 全部消去线性基 $ B $ 中的位后，直接快速匹配就行了 $ KMP $

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
#include <bits/stdc++.h>
#define ll long long
namespace FAST_IO
{
    template <class T>
    inline void read(T &x)
    {
        T flag = 1;
        x = 0;
        char ch = getchar();
        while (ch < '0' || ch > '9')
        {
            if (ch == '-')
                flag = -1;
            ch = getchar();
        }
        while (ch >= '0' && ch <= '9')
        {
            x = (x << 3) + (x << 1) + (ch ^ 48), ch = getchar();
        }
        x *= flag;
    }

    template <class T, class... _T>
    inline void read(T &x, _T &... y)
    {
        return read(x), read(y...);
    }

} // namespace FAST_IO
using namespace std;
using namespace FAST_IO;
const ll mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const ll INF_LL = 0x3f3f3f3f3f3f3f3f;
const double eqs = 1e-5;
const int maxn = 2e5 + 10;
const int maxm = 1e5 + 10;
int t, n, m, k;

struct LinearBase
{
    const static int LEN = 35;
    int v[LEN];
    void init() { memset(v, 0, sizeof(v)); };
    void insert(int x)
    {
        for(int i = 31; i >= 0; i--)
        {
            if((x>>i) & 1)
            {
                if(v[i]) x ^= v[i];
                else
                {
                    v[i] = x;
                    break;
                }
            }
        }
    }

    int solve(int x)
    {
        for (int i = 30; i >= 0; i--)
            if (x >> i & 1)
                x ^= v[i];
        return x;
    }
}B;
int a[maxn], b[maxn], s[maxn];
int Next[maxn];
void getNext()
{
    Next[1] = 0;
    for (int i = 2, j = 0; i <= m; i++)
    {
        while (j > 0 && b[j + 1] != b[i])
            j = Next[j];
        if (b[j + 1] == b[i])
            j++;
        Next[i] = j;
    }
}

int kmp()
{
    int n2 = 1, ans = 0;
    for (int i = 1, j = 0; i <= n; i++)
    {
        while (j > 0 && b[j + 1] != a[i])
            j = Next[j];
        if (b[j + 1] == a[i])
            j++;
        if (j == m)
        {
            ans = (ans + n2) % mod;
            j = Next[j];
        }
        if (i >= m)
            n2 = (2LL * n2) % mod;
    }
    return ans;
}


int main()
{
// #define COMP_DATA
#ifndef ONLINE_JUDGE
#ifdef COMP_DATA
    freopen("/mnt/f/文档/课件/ACM比赛/2020hdu多校/第四场/data/E.in", "r", stdin);
    freopen("out.txt", "w", stdout);
#else
    freopen("in.txt", "r", stdin);
#endif
#endif

    int tcase;
    read(tcase);
    while (tcase--)
    {
        read(n, m, k);
        B.init();
        for(int i = 1; i <= n; i++)
        {
            read(a[i]);
        }
        for (int i = 1; i <= m; i++)
        {
            read(b[i]);
        }
        for (int i = 1; i <= k; i++)
        {
            read(s[i]);
            B.insert(s[i]);
        }

        for(int i = 1; i <= n; i++)
        {
            a[i] = B.solve(a[i]);
        }
        for (int i = 1; i <= m; i++)
        {
            b[i] = B.solve(b[i]);
        }
        getNext();
        printf("%d\n", kmp());
    }
    return 0;
}