A. Tetrahedron
题目描述:
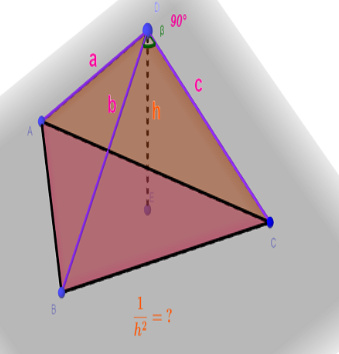
一个四面体,顶角是三个直角。给出一个 $ n $ ,三个直角边边长 $ a, b, c \in [1,n] $ ,顶点到地面的高 $ h $ ,求 $ \frac{1}{h^2} $ 的期望。
数据范围:
题解:
看这个图就很迷惑,刚开始以为 $ h $ 直接是补成长方体后的对角线的一半。后来发现是高。原本的方法是使用体积相等求出 $ h $ ,底面面积使用海伦公式计算。后来发现有个定理。
定理:直角三棱锥的三个直角面面积的平方和等于底面面积的平方。
证明:
可以使用海伦公式体积相等证明一波
直接使用几何知识证明
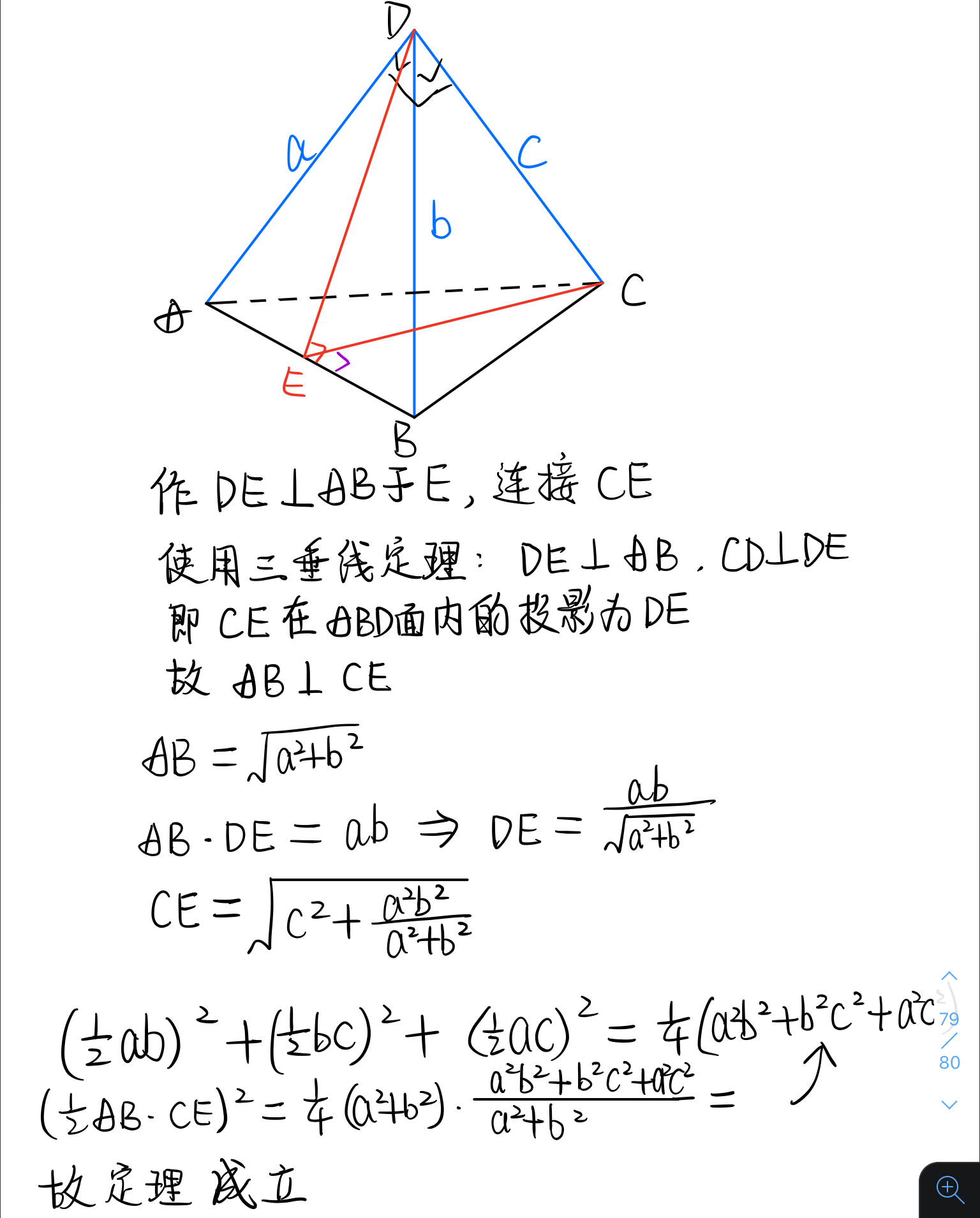
知道这个定理之后就好办了。一波代换化简就可以得到 $ \frac{1}{h^2} = \frac{1}{a^2} + \frac{1}{b^2} + \frac{1}{c^2} $
故 $ E(\frac{1}{h^2}) = 3E(\frac{1}{a^2}) = 3 \times \frac{1}{n} \sum_{i=1}^n \frac{1}{i^2} $
所以线性求逆元,然后平方一下,再求一下前缀和
代码:
1 |
|
B. Funny String
题目描述:
数据范围:
题解:
需要使用后缀数组,刚好之前写过模板。
代码:
1 |
C. Boring Game
题目描述:
$ n $ 张纸折叠 $ k $ 次,然后从上往下标 $ 1-n $ ,求展开之后的序列。

数据范围:
$ 1\le T \le 30 \\ 1\le n \le 200, 1\le k \le 10 \\ \sum 2\times n \times 2^k \le 10^6 $
题解:
直接模拟,将上半部分反转放在左侧,想象 $ n $ 张纸展开的情况,每次截取上半部分,倒置(左转 $ 90 $ 度)后将其放置于剩余部分的左侧,模拟 $ k $ 次即可
代码:
1 |
|
D.
题目描述:
数据范围:
题解:
代码:
1 |
E.
题目描述:
数据范围:
题解:
代码:
1 |
F.
题目描述:
数据范围:
题解:
代码:
1 |
G. Tree
题目描述:
一棵无根树,带有边权。找出一个连通子图,权值最大,而且度数超过 $ k $ 的结点最多只有一个。
数据范围:
$ 1\le n \le 2 \times 10^5 ,0\le k \le n \\ 1\le u, v\le n ,0\le d \le 10^9 \\ \sum n \le 10^6 $
题解:
看着应该像是一个树形 $ dp $ 的题目,奈何树形 $ dp $ 不太会,所以不知道怎么搞。后面学习树形 $ dp $ 再好好看看
题解中的方法:
首先 $ k=0 $ 时答案显然为 $ 0 $
对于最终所求的连通块,要求不超过一个点的度大于 $ k $ ,其余点的度均小于等于 $ k $ 的树,采用树形 $ dp $ 。
首先将原树看成一颗有根树,根节点任意:
- 我们假设 $ dp[x] [0] $ 表示 $ x $ 为根节点,所有节点儿子数量均小于等于 $ k-1 $ 的点的子连通图最大边权和。
- $ dp[x] [1] $ 表示 $ x $ 点为根节点,有不超过 $ 1 $ 个节点儿子数量大于 $ k-1 $ ,其余节点儿子个数等小于等于 $ k-1 $ 的子连通图最大边权和。
- 只要保证点儿子数量均不超过 $ k-1 $ ,那么显然该点度不会超过 $ k $ 。
转移方程:
假设 $ x $ 有 $ c $ 个儿子,表示为 $ s_1,s_2….s_c $ ,我们首先将儿子节点按 $ dp[s_i] [0] $ 由大到小排序。
可以得到 $ dp[x][0]= \sum_{i=1}^{k-1}dp[s_i][0]+w_{xs_i} $ ,其中 $ w_{xs_i} $ 表示 $ x $ 到 $ s_i $ 点的边的边权。
而对于 $ dp[x] [1] $ ,由于度大于 $ k $ 的不超过一个,那最多只能有 $ 1 $ 个点儿子数量大于 $ k-1 $
若该点为 $ x $ 点,则有
而若该点为x点的子孙节点,则选取 $ x $ 的 $ k-2 $ 个儿子的 $ dp[0] $ 以及 $ 1 $ 个儿子的 $ dp[1] $ ,可以先贪心的将最大的 $ k-2 $ 个 $ dp[0] $ 取下,由于 $ dp[1] $ 只需要取一个,那么有两种取法:
第一种为取前 $ k-1 $ 个点中的某点的 $ dp[1] $ ,那么 $ dp[0] $ 就少了一个,需要将 $ dp[s_{k-1}][0] $ 一并选取,即有
第二种为取 $ k-2 $ 个节点后的某个节点,有
最终方案显然是可以选取某个点的 $ dp[x][1] $ ,但是存在一种情况,即选取了某一个节点和其 $ k $ 个子树,而没有将联通块和该节点的父亲节点相连,这时候答案为该节点的 $ k-1 $ 个儿子节点 $ s_i $ 的 $ dp[s_i][0] $ 以及一个儿子节点的 $ dp[s_i][1] $ 组成,做法和求该节点 $ dp[x][1] $ 相同,只是多选了一个儿子节点的 $ dp[0] $ 而已,在 $ dfs $ 的时候顺便求了即可。
时间复杂度为 $ O(n \log n) $
代码:
题解代码
1 |
|
H.
题目描述:
数据范围:
题解:
代码:
1 |
I. Paperfolding
题目描述:
一张纸,有 $ n $ 次操作,每次可以选择横折或竖折,最后从中间切个十字形,得到若干纸片。问纸片数量的期望。
数据范围:
$ 1\le T \le 10^5 \\ 0\le n \le 10^{18} \\ mod (998244353) $
题解:
对于横折 $ x $ 竖折 $ y $ 可以得到 $ (2^x + 1)(2^y + 1) $ , $ x+y = n $
期望为
需要使用错位相减法进行求解,然后使用二项式定理合并。
得到公式后由于只涉及到 $ n $ ,所以直接快速幂就行了。
代码:
1 |
|
J.
题目描述:
数据范围:
题解:
代码:
1 |
K. Exam
题目描述:
$ n $ 场考试,每个考试有两个时间段 $ [a, a+at] $ , $ [b, b + bt] $ ,选择一个时间段参加,而且两场考试的时间不能重叠,就是不能有交集。如果可以找到方案则输出最早的结束时间,否则输出 $ -1 $
数据范围:
$ T \\ 1\le n \le 25000 \\ 0\le a, at, b,bt \le 10^9 \\ \sum n \le 10^5 $
$ time\ limit:5500ms $
题解:
很明显能否找到是一个是一个 $ 2-sat $ 问题,但是需要找出最早的结束时间,发现该时间满足单调性,可以使用二分答案。
设 $ [a,a+at] $ 选择与否为变量 $ i $ , $ [b,b+bt] $ 选择与否为变量 $ i’ $
$ \to $ 表示连边,假设当前二分的值为 $ mid $ ,如果 $ a+at>mid $ ,则说明考试 $ i’ $ 是必选的, $ i \to i’ $ ,如果 $ b+bt>mid $ ,则说明考试 $ i $ 是必选的, $ i’ \to i $ 。
剩下只需要将有冲突的考试进行连边。
如果 $ [a_i,a_i+at_i] $ 与 $ [a_j,a_j+at_j] $ 有交,则说明是冲突的, $ i \to j’ , j \to i’ $ 。
如果 $ [a_i,a_i+at_i] $ 与 $ [b_j,b_j+bt_j] $ 有交,则说明是冲突的, $ i \to j , j’ \to i’ $ 。
如果 $ [b_i,b_i+bt_i] $ 与 $ [a_j,a_j+at_j] $ 有交,则说明是冲突的, $ i’ \to j’ , j \to i $ 。
如果 $ [b_i,b_i+bt_i] $ 与 $ [b_j,b_j+bt_j] $ 有交,则说明是冲突的, $ i’ \to j , j’ \to i $ 。
显然直接暴力建边的话时间和空间复杂度都是 $ n^2 $ 的。
对于每一场考试 $ i $ ,我们发现只需要考虑其他的考试 $ j $ , $ a_i \leqslant a_j \leqslant a_i+at_i $ ,就可以包括所有情况
如果将所有考试按开始时间排序,注意到与每一场考试 $ i $ 有冲突考试 $ j $ 都是一段连续的区间
可以通过线段树优化建图在 $ n \log n $ 的时间内完成建图
时间复杂度 $ O( n \log^2 n ) $
- 空间复杂度 $ O( n \log n ) $
代码:
1 |
|
L. Set1
题目描述:
给定一个 $ 1-n $ 的集合S,每次删除当前集合中最小的元素,再随机删掉 $ 1 $ 个元素,直到 $ |S| = 1 $ ,求每个元素最后被留下来的概率。
数据范围:
$ 1\le T \le 40\\ 1\le \sum n \le 5\times 10^6 \\ mod(998244353) $
题解:
首先前一半元素概率为零。
对于元素 $ i $ ,前面有 $ i-1 $ ,后面有 $ n-i $ ,当 $ n-i \le i-1 $ 时, $ i $ 才可能留下。
从前面选 $ n-i $ 个和后面的对应将后面的删掉 $ C_{i-1}^{n-i} \times (n-1)! $ 注意阶乘,对后面的全排列一下进行对应
对于前面剩下的没有匹配的 $ i-1 - n + i = 2 \times i - n - 1 $ 个元素两两配对
因此 $ i $ 被留下的方案数为
总方案数为 $ sum = \sum_{i=1}^{n} cnt[i] $
其实也可以打表,就类似 $ dp $ 那样
代码:
1 |
|