Luobuyu's Blog

0%

hdu多校(第三场)

发表于 分类于 ， 热度： ℃ 评论：
本文字数： 8.4k 阅读时长 ≈ 8 分钟
2020年hdu暑期多校训练(第三场)，有些题目想复杂了

A.

题目描述：

数据范围：

题解：

代码：

1
2


B.

题目描述：

数据范围：

题解：

代码：

1
2


C.

题目描述：

数据范围：

题解：

代码：

1
2


D. Tokitsukaze and Multiple

题目描述：

给出一个长度为 $ n $ 的序列，给出一个模数 $ p $ 。序列中连续的两个可以合并，可以多次合并，计算最多有多少个 $ \mod {p} =0 $

数据范围：
$ 1\le T \le 20 $

$ 1\le n,p\le10^5,\sum n \le 10^6 $

$ 1\le a_i \le 10^5 $

题解：

本质上是让给序列分段，最多有多少段能够被 $ p $ 整除。由于需要使用到和，所以可以使用前缀和 $ sum $ 维护。 对前缀和中每一个数取一下模，然后满足的就是前缀和序列中两个值相等的情况，两值相等说明中间的和刚好可以被 $ p $ 整除。 $ dp $ 可以解决，使用一个数组保存 $ pre[sum[i]] $ 。 $ dp[i] = max(dp[i-1], dp[pre[sum[i]]] + 1) $

也可以贪心的搞，由于每一段都是非连续的，所以可以把当前出现的全部存起来，然后遇到重复的搞一下，删除全部的。使用 $ map $

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e5 + 10;
// F:\文档\课件\ACM比赛\2020hdu多校\第三场\data
int t;
int n, p;
int a[maxn];
int dp[maxn];
int last[maxn];
int main()
{
#ifndef ONLINE_JUDGE
    #ifdef COMP
        freopen("/mnt/f/文档/课件/ACM比赛/2020hdu多校/第三场/data/1004.in", "r", stdin);
        freopen("out.txt", "w", stdout);
    #else
        freopen("in.txt", "r", stdin);
    #endif
#endif
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> t;
    while(t--)
    {
        cin >> n >> p;
        for(int i = 1; i <= n; i++) 
        {
            cin >> a[i];
            a[i] = (a[i - 1] + a[i]) % p;
        }
        memset(last, -1, sizeof(last));
        last[0] = 0;
        dp[0] = 0;
        for (int i = 1; i <= n; i++)
        {
            dp[i] = dp[i-1];
            if(last[a[i]] != -1)
            {
                dp[i] = max(dp[i], dp[last[a[i]]] + 1);
            }
            last[a[i]] = i;
        }
        cout << dp[n] << endl;
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e5 + 10;
int t;
int n, p;
int a[maxn];
int dp[maxn];
int last[maxn];
map<int, int> mp;
int main()
{
#ifndef ONLINE_JUDGE
    #ifdef COMP
        freopen("/mnt/f/文档/课件/ACM比赛/2020hdu多校/第三场/data/1004.in", "r", stdin);
        freopen("out.txt", "w", stdout);
    #else
        freopen("in.txt", "r", stdin);
    #endif
#endif
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> t;
    while(t--)
    {
        cin >> n >> p;
        for(int i = 1; i <= n; i++) 
        {
            cin >> a[i];
            a[i] = (a[i - 1] + a[i]) % p;
        }
        mp.clear();
        mp[0] = 1;
        int ans = 0;
        for (int i = 1; i <= n; i++)
        {
            if(mp.count(a[i]))
            {
                ans++;
                mp.clear();
            }
            mp[a[i]] = 1;
        }
        cout << ans << endl;
    }
    return 0;
}

E. Little W and Contest

题目描述：

$ 1 $ 号表示读题手， $ 2 $ 号表示代码手。从 $ n $ 个人中选出队员组成队伍。增加人之间的熟悉关系，具有传递性。限制如下：

  • 一个队伍至少有两名代码手
  • 队伍内部不能有相互熟悉的人。

求有多少种组合 $ (\mod (1e9 + 7)) $

数据范围：
$ 1\le T \le 10 $

$ 1\le n \le 10^5 $

题解：

之前我也想到了使用并查集维护，每个并查集集合记录 $ 1 $ 的人数， $ 2 $ 的人数。先算出来，然后增加关系的时候再减去一部分。

假设目前有两个集合。 $ \{a_1, a_2\} $ ， $ \{b_1, b_2\} $

合并的时候需要减去一部分

左 $ 1 $ 右 $ 2 $ 余 $ 2 $

左 $ 2 $ 右 $ 1 $ 余 $ 2 $

左 $ 2 $ 右 $ 2 $ 余 $ 2 $

左 $ 2 $ 右 $ 2 $ 余 $ 1 $

总共需要减去这四种

算初始的 $ sum $ 出现了一些问题。在除之前不能使用 $ mod $ 。因为除法不满足类似 $ (a\times b) mod(c) = a \mod(c)\times b \mod (c) $ 的性质

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e5 + 10;
const ll mod = 1e9 + 7;
int fa[maxn], a[maxn][2];
int findFa(int u) { return fa[u] == u ? u : (fa[u] = findFa(fa[u])); }

int t, n, m;

void init()
{
    for (int i = 0; i <= n; i++)
    {
        a[i][0] = a[i][1] = 0;
        fa[i] = i;
    }
}
int main()
{
#ifndef ONLINE_JUDGE
    freopen("/mnt/f/文档/课件/ACM比赛/2020hdu多校/第三场/data/1005.in", "r", stdin);
    
    freopen("out.txt", "w", stdout);
    // freopen("in.txt", "r", stdin);
#endif
    scanf("%d", &t);
    int x;
    
    while (t--)
    {
        scanf("%d", &n);
        init();
        int one = 0, two = 0;
        for (int i = 1; i <= n; i++)
        {
            scanf("%d", &x);
            if (x == 1)
                one++;
            else
                two++;
            x--;
            a[i][x]++;
        }
        ll sum = (two * (two - 1LL)  * (two - 2LL)  / 6 % mod + two * (two - 1LL)  * one / 2 % mod) % mod;
        printf("%lld\n", sum);
        int u, v;
        for (int i = 1; i < n; i++)
        {
            scanf("%d%d", &u, &v);
            u = findFa(u);
            v = findFa(v);

            sum = ((sum - ((ll)a[u][0] * a[v][1] % mod * (two - a[u][1] - a[v][1]) % mod)) % mod + mod) % mod; // 左1右2余2
            sum = ((sum - ((ll)a[u][1] * a[v][0] % mod * (two - a[u][1] - a[v][1]) % mod)) % mod + mod) % mod; // 左2右1余2
            sum = ((sum - ((ll)a[u][1] * a[v][1] % mod * (two - a[u][1] - a[v][1]) % mod)) % mod + mod) % mod; // 左2右2余2
            sum = ((sum - ((ll)a[u][1] * a[v][1] % mod * (one - a[u][0] - a[v][0]) % mod)) % mod + mod) % mod; // 左2右2余1
            printf("%lld\n", sum);
            
            a[v][0] += a[u][0];
            a[v][1] += a[u][1];
            fa[u] = v;
        }
    }

    return 0;
}

F.

题目描述：

数据范围：

题解：

代码：

1
2


G. Tokitsukaze and Rescue

题目描述：

一个无向完全图，任意两点之间都有一条边，带边权。

删除 $ k $ 条边之后的最短路最大值。

数据范围：
$ 1\le T \le 100 $

$ 3\le n \le 50, 1\le k \le min(n-2, 5) $

$ 1\le w \le 10^4 $

题解：

image-20200729190342069没想到题解还真是枚举删除，变成了搜索问题了。

注意记录路径开的 $ pre $ 数组如果开为全局需要使用二维的，防止不同的 $ dfs $ 深度对其破坏。也可以直接使用局部的，拷贝一下。

$ wsl $ 跑的也太慢了，跑了 $ 30s $ 左右，交上去居然过了，才跑了 $ 5s $ 多。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include <bits/stdc++.h>
#define ll long long
using namespace std;
typedef pair<int, int> pii;
const int maxn = 50 + 10;
const ll mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;
const double eqs = 1e-5;
int t, n, k, m;
int g[maxn][maxn];
int ans;
int pre[maxn][maxn];
int dis[maxn];
int now;
void dijstra(int s, int cur)
{
    priority_queue<pii, vector<pii>, greater<pii>> q;
    memset(dis, 0x3f, sizeof(dis));
    dis[s] = 0;
    q.push(make_pair(0, s));
    while (!q.empty())
    {
        pii out = q.top();
        q.pop();
        int u = out.second;
        if (dis[u] < out.first)
            continue;
        for (int i = 1; i <= n; i++)
        {
            if (g[u][i] == inf || g[u][i] == 0)
                continue;
            if (dis[i] > dis[u] + g[u][i])
            {
                dis[i] = dis[u] + g[u][i];
                pre[cur][i] = u;
                q.push(make_pair(dis[i], i));
            }
        }
    }
}

void dfs(int cur)
{
    dijstra(1, cur);
    if (cur == k + 1)
    {
        ans = max(ans, dis[n]);
        return;
    }
    int v = n, u;
    while (v != 1)
    {
        u = pre[cur][v];
        int tmp = g[u][v];
        g[u][v] = g[v][u] = inf;
        dfs(cur + 1);
        g[u][v] = g[v][u] = tmp;
        v = u;
    }
}

int main()
{
#ifndef ONLINE_JUDGE
    freopen("/mnt/f/文档/课件/ACM比赛/2020hdu多校/第三场/data/1007.in", "r", stdin);
    freopen("out.txt", "w", stdout);
    // freopen("in.txt", "r", stdin);
#endif
    scanf("%d", &t);
    int u, v, w;
    while (t--)
    {
        scanf("%d %d", &n, &k);
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                g[i][j] = i == j ? 0 : inf;
        for (int i = 1; i <= n * (n - 1) / 2; i++)
        {
            scanf("%d%d%d", &u, &v, &w);
            g[u][v] = g[v][u] = w;
        }
        ans = 0;
        dfs(1);
        printf("%d\n", ans);
    }
    return 0;
}

H. Triangle Collision

题目描述：

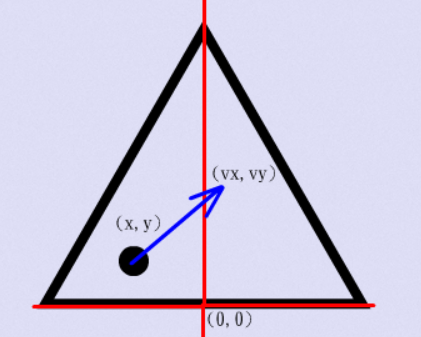
image-20200729215433868

一个等边三角形，给出其中一个点的初始速度 $ v_x, v_y $ ，碰到边界发生碰撞，遵循反射定律。求第 $ k $ 次碰撞发生的时间。保证了不会撞到角中。

数据范围：
$ 1\le T \le 10^4 $

$ 1\le L \le 10^4, -10^4 \le x, y, v_x, v_y \le 10^4 $

$ 1\le k \le 10^6 $

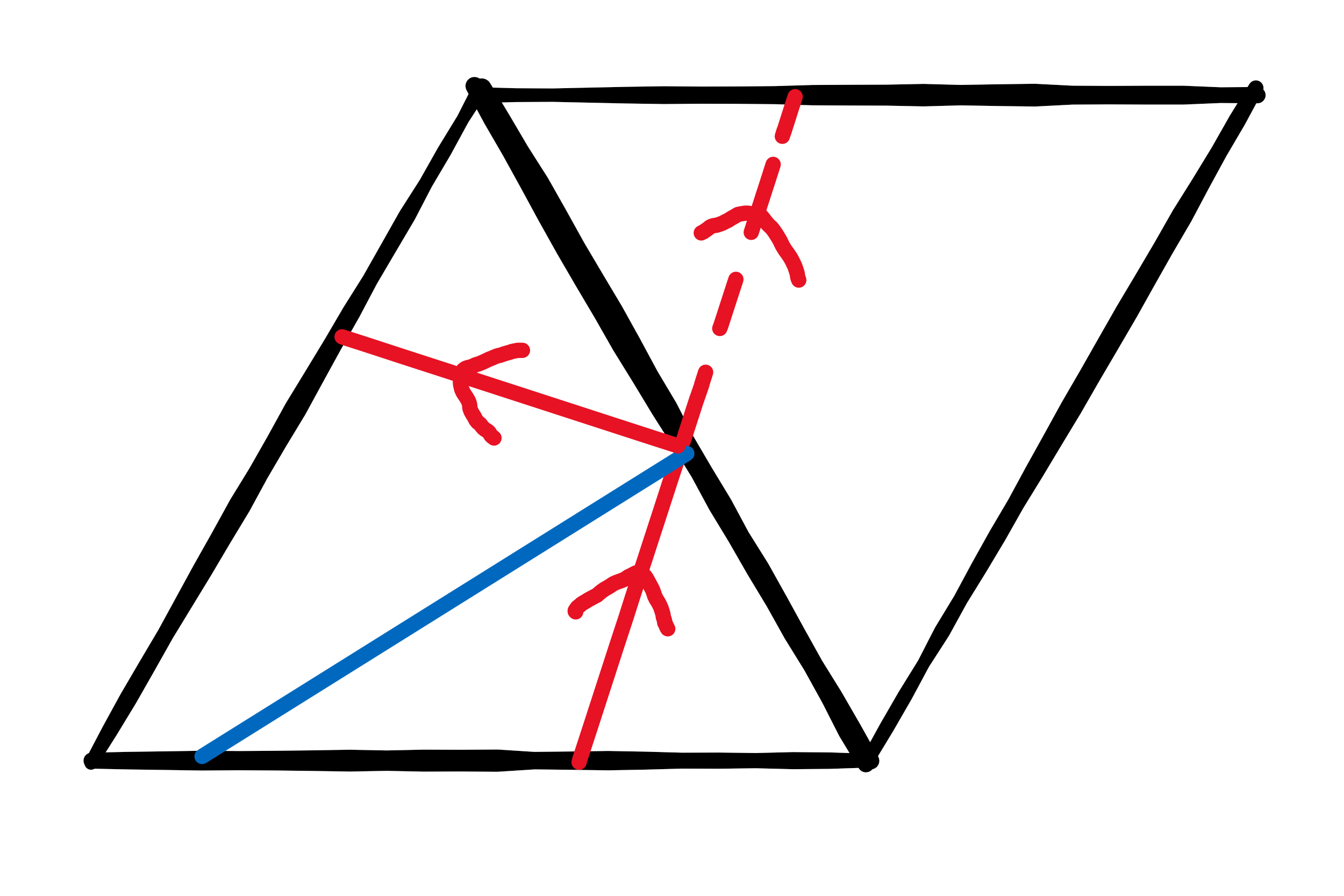
题解：

很明显需要考虑将三角形翻折镜像等操作，让小球一直沿着直线跑。

二分答案。

首先考虑与 $ x $ 轴平行的先，只需要看 $ vy $ 就可以算，然后将速度和坐标旋转一下，继续同样的方法处理。

image-20200729220555141

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<bits/stdc++.h>
using namespace std;
const int MAXN=10005;
const double EPS=1e-6;
const double PI=4.0*atan(1.0);
const double base=2*PI/3;
int k,T;
double L,vx,vy,x,y,h;
pair<double,double> get_point(const pair<double,double> &a,const double &rad)
{
    return make_pair(a.first*cos(rad)-(a.second-h/3)*sin(rad),a.first*sin(rad)+(a.second-h/3)*cos(rad)+h/3);
}
bool ck(double times)
{
    long long has=0;
    has+=abs(floor(get_point(make_pair(x+vx*times,y+vy*times),base*0).second/h));
    has+=abs(floor(get_point(make_pair(x+vx*times,y+vy*times),base*1).second/h));
    has+=abs(floor(get_point(make_pair(x+vx*times,y+vy*times),base*2).second/h));
    return has>=k;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%lf %lf %lf %lf %lf %d",&L,&x,&y,&vx,&vy,&k);
        h=L*sqrt(3)/2;

        double l=0,r=1e11,mid;
        while(r-l>EPS)
        {
            mid=(l+r)/2;
            if(ck(mid)) r=mid;
            else l=mid;
        }
        printf("%.8lf\n",(l+r)/2);
    }
    return 0;
}

I. Parentheses Matching

题目描述：

给出一个序列，全是 $ () $ ，然后将 $ $ 替换，或者把 $ * $ 删去，能否得到一个匹配好的序列。按照字典序最小，选出字典序最小的。

数据范围：
$ 1\le T \le 10^5 $

$ 1\le n \le 10^5,\sum n \le 5 \times10^6 $

题解：

image-20200729162008862

这是题解中的证明。左侧是补 $ ( $ ，右侧是补 $ ) $

所以可以使用队列把 $ * $ 存起来，遇到不够的时候就拿出来补

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e5 + 10;
int t, n;
queue<int> q;
char s[maxn];
int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> t;
    while (t--)
    {
        cin >> s;
        int sum = 0;
        n = strlen(s);
        while(q.size())
            q.pop();
        for (int i = 0; i < n; i++)
        {
            if (s[i] == '(')
                sum++;
            else if (s[i] == '*')
                q.push(i);
            else sum--;
            if(sum < 0)
            {
                if(q.empty())
                    break;
                s[q.front()] = '(', q.pop();
                sum++;
            }
        }
        if(sum < 0) 
        {
            cout << "No solution!" << endl;
            continue;
        }

        if(sum == 0)
        {
            for (int i = 0; i < n; i++)
            {
                if (s[i] != '*')
                {
                    cout << s[i];
                }
            }
            cout << endl;
            continue;
        }

        sum = 0;
        while(q.size())
            q.pop();
        for (int i = n - 1; i >= 0; i--)
        {
            if(s[i] == '*') q.push(i);
            else if(s[i] == '(') sum--;
            else
                sum++;
            if(sum < 0)
            {
                if(q.empty())
                    break;
                s[q.front()] = ')';
                q.pop();
                sum++;
            }
        }
        if (sum < 0)
        {
            cout << "No solution!" << endl;
            continue;
        }

        for(int i = 0; i < n; i++)
        {
            if(s[i] != '*')
            {
                cout << s[i];
            }
        }
        cout << endl;
    }
    return 0;
}

J.

题目描述：

数据范围：

题解：

代码：

1
2